8.10. Приведенное количество тепла. Неравенство Клаузиуса

Коэффициент полезного действия для любой тепловой машины

,

где Q₁ - количество теплоты, отданное нагревателем, Q₂ - отданное холодильнику.

Коэффициент полезного действия обратимой тепловой машины (цикл Карно)

,

где Т₁ – температура нагревателя, Т₂ – температура холодильника.

В случае обратимого процесса между этими величинами должен стоять знак равенства:

(8.9)

В случае необратимого процесса – знак неравенства:

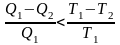(8.10)

Соотношения (8.9) и (8.10) можно объединить и записать в виде

или .

Умножив полученное выражение на положительную величину , получим

.

Вычитая из левой и правой части 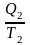, имеем

. (8.11)

В соотношение (8.11) входит как тепло, полученное системой Q₁, так и тепло, отдаваемое ею Q₂. Вместо отдаваемого телу тепла Q₂ введем полученное от этого тела тепло, равное -Q₂. Тогда выражение (8.11) запишется в виде

. (8.12)

Это соотношение носит название неравенства Клаузиуса.

Отношение количества тепла, полученного системой от какого-либо тела, к температуре этого тела называется приведенным количеством тепла. Используя эту терминологию Клаузиуса, выражение (8.12) может быть сформулировано следующим образом: при обратимом цикле Карно сумма приведенных количеств тепла равно нулю, при необратимом цикле – меньше нуля.

Неравенство Клаузиуса может быть обобщено на любой круговой процесс. Любой круговой процесс может быть разбит на весьма большое число элементарных циклов Карно. Каждый из этих элементарных циклов Карно протекает между нагревателем соответствующей температуры T_i, от которого он получает количество тепла Q_i, и холодильником соответствующей температуры T_k, которому он отдает количество тепла Q_k. Для этого элементарного цикла напишем неравенство Клаузиуса:

. (8.13)

Суммируя выражение (8.13), написанное для каждого из элементарных циклов, получим для всего цикла

. (8.14)

Т.е. для всякого кругового процесса сумма приведенных количеств тепла не может быть больше нуля. В случае обратимого протекания процесса можно показать, что сумма (8.14) преобразуется в контурный интеграл

,

где интеграл берется по всему циклу.

164