
- •8.4. Применение первого начала термодинамики к изопроцессам в газах
- •8.4.1. Изохорный процесс
- •8.4.2. Изотермический процесс
- •8.4.3. Изобарный процесс
- •8.5. Адиабатический процесс
- •8.6. Круговые, необратимые и обратимые процессы
- •8.7. Цикл Карно
- •8.8. Принцип действия тепловой и холодильной машин
- •8.9. Второе начало термодинамики
- •8.10. Приведенное количество тепла. Неравенство Клаузиуса
8.4. Применение первого начала термодинамики к изопроцессам в газах
8.4.1. Изохорный процесс
Процесс, протекающий при V=const, называется изохорным. Поскольку при изохорном процессе V=const, а dV=0, то dA=pdV=0, т.е. при изохорном процессе газ работу не совершает. Первое начало термодинамики запишется в этом случае в виде соотношения
dU = dQ.
Количество теплоты, которое необходимо сообщить системе для того, чтобы при постоянном объеме повысить его температуру на величину dT, можно выразить, если известна теплоемкость вещества при постоянном объеме dQ=CVdT и, следовательно, dU=CVdT. Принимая, что CV - теплоемкость идеального газа не зависит от температуры, для внутренней энергии идеального одноатомного газа получим выражение
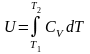 .
.
Для
 киломолей
киломолей
 .
.
Таким образом,
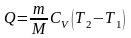 ,
,
т.е. при изохорном изменении состояния газа вся подведенная к системе теплота идет на увеличение внутренней энергии системы.
8.4.2. Изотермический процесс
Процесс, происходящий при постоянной температуре, называется изотермическим процессом. При
T = const, U = const, dU = 0.
Уравнение первого начала термодинамики при изотермическом состоянии газа запишется в следующей форме:
dQ = dA. (8.3)
Из этого выражения следует, что при изотермическом процессе все подводимое к системе количество теплоты превращается в работу. Для подсчета работы, совершенной газом при изотермическом расширении от объема V1 до V2, необходимо проинтегрировать выражение для элементарной работы:
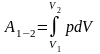 .
.
Выразив давление из уравнения Менделеева-Клайперона для одного моля газа
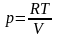
и подставив в уравнение для определения работы, получим
 ,
,
 .
.
Работа, совершаемая при расширении -молей газа, будет в раз больше, т.е.
 .
.
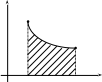
Графически
вычисленная работа (рис.8.6) выражается
на диаграмме с координатами pV
площадью аbcd,
заштрихованной на графике. Вместо
отношения
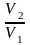 ,
можно воспользоваться равным ему
обратным отношением давлений, исходя
из закона Бойля-Мариотта, тогда
,
можно воспользоваться равным ему
обратным отношением давлений, исходя
из закона Бойля-Мариотта, тогда
Согласно (8.3), при T=const Q=A, т.е.
|
a
b
d c V1 V2 V Рис.8.6 |
8.4.3. Изобарный процесс
Изобарный процесс – процесс, происходящий при постоянном давлении p=const. Работа в этом случае равна
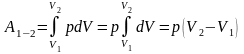 .
.
Работа изображается на диаграмме (рис.8.7.) площадью прямо-угольника abcd.
Применим первое начало термодинамики к изобарному процессу dQ = dU + dA. Из определения молярной теплоемкости следует, что dQ = CpdT. Интегрируя выражение, по-лучим количество теплоты, необходимое для нагревания газа от температуры T1 до T2 для од- |
a b
d c V1 V2 V Рис.8.7
|
ного моля газа
 ,
,
для
молей газа
 .
.
Таким образом, при изобарном процессе подводимое к газу тепло частично тратится на увеличение его внутренней энергии и частично на совершение работы.
При изобарном сжатии направление процесса меняется на обратное и работа, совершенная газом становится отрицательной dA0. Это означает, что не газ совершает внешнюю работу, а внешние силы совершают положительную работу dA по сжатию газа, т.е.
dA = dA.
Величина dU и dQ при этом также отрицательны, т.е. внутренняя энергия газа уменьшается за счет отдачи им тепла окружающим телам.

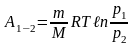 .
. .
. p
p р
р