Физико- математическая модель и алгоритм расчета

Рассмотрим длинную цилиндрическую изложницу 1 с внутренним радиусом R₂ и внешним радиусом R₃, которая в начальный момент времени заполняется расплавом.

Внешняя поверхность изложницы охлаждается, в результате чего в расплаве начинается направленный процесс кристаллизации.

Чтобы сохранить изложницу от сильных температурных воздействий, ее внутреннюю (рабочую) поверхность покрывают слоем краски или облицовочной смеси 2. Кроме этого, в результате термического расширения изложницы и усадочных явлений в затвердевшем металле 4 между изложницей и металлом может возникнуть газовый зазор 3, влияющий на условия теплообмена в системе.

Поскольку изложница достаточно длинная, мы ограничимся рассмотрением процесса в некотором ее поперечном сечении, пренебрегая торцевыми эффектами. Кроме этого, будем считать задачу симметричной и не учитывать термоконвективные токи в расплаве. Расчетная схема задачи показана на рис.17.

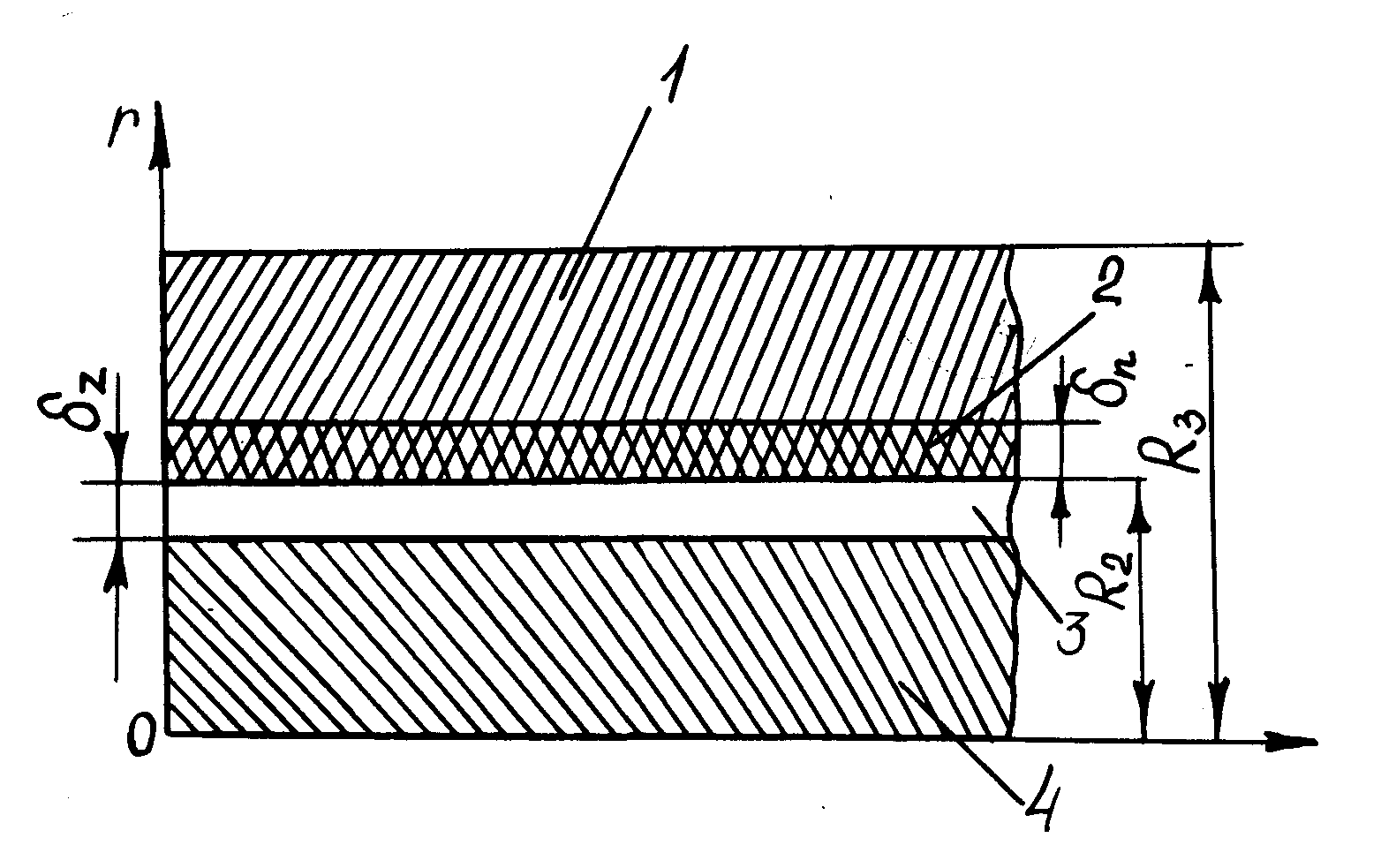
Рис.17 Схема к расчету затвердевания отливки в форме

С учетом сделанных предположений теплоперенос в затвердевающем расплаве описывается уравнением теплопроводности [8]

  0, 0 r  R₂ , r₁  r  r₂ (1 )

с условием на подвижной границе фазового перехода r = ():

r = , T(, ) = T_ф , (2 )

где  - координата фронта затвердевания, разделяющая жидкую и твердую фазы металла (параметры, относящиеся к жидкой и твердой фазам, обозначаются соответственно индексами «ж» и «т»; L – удельная теплота кристаллизации; T_ф - температура фазового перехода.

Рассматриваемую задачу теплопроводности с нелинейным условием на подвижной неизвестной границе фаз обычно называют задачей Стефана. Решение ее представляет серьезные математические трудности. Одним из конструктивных подходов в этом вопросе является учет тепловыделений на фронте кристаллизации в эффективной теплоемкости. С этой целью вводится в рассмотрение -функция Дирака:

Теперь условия на фронте кристаллизации (2) будут учтены, если уравнение (1) заменить уравнением

(3 )

Произведя сглаживания коэффициентов на некотором интервале температур T_ф-, T_ф+ и заменяя -функцию Дирака -образной функцией

приходим к уравнению

формально совпадающему с (1), где, однако, введена эффективная теплоемкость:

( 4 )

К аналогичной математической формулировке задачи можно прийти, если учитывать тепловыделение в затвердевающем расплаве при наличии двухфазной зоны кристаллизации, определяемой температурами солидуса ( Т_S ) и ликвидуса ( Т_L ) в соответствии с диаграммой состояния расплава. В этом случае можно считать Т_ф -  = Т_S,, T_ф +  = Т_L и задаться вполне определенным видом -образной функции, исходя из аналитических зависимостей для линий солидус и ликвидус расплава.

Перейдем к формулировке краевой задачи для системы тел «затвердевающий расплав» - «изложница». Условимся в дальнейшем параметры, относящиеся к расплаву, обозначать индексом «1», а параметры, относящиеся к изложнице, - «2».

Распределение температур в системе описывается одномерными нестационарными уравнениями теплопроводности

(5 )

j = 1, c₁= c_эф

с начальными условиями

Т_j (r, 0) = T_0j(r), j = 1, 2, (6 )

условием симметрии температурного поля на оси цилиндра

при r = 0,

условием конвективного теплообмена на внешней поверхности цилиндра с некоторой охлаждающей жидкостью, температуру Т₀:

при r = R₃, ( 7 )

а также условиями сопряжения на внутренней поверхности изложницы, которые можно получить следующим образом.

Теплообмен между изложницей и расплавом осуществляется через двухслойную «контактную зону», состоящую из слоя теплоизоляции толщиной _п и зазора толщиной _z= _z(), которую мы считаем заданной функцией времени. Считая процесс теплопереноса через двухслойную зону квазистационарным, для плотностей тепловых потоков, проходящих через покрытие и зазор, можно записать

(8)

(9)

где _п, _z- теплопроводности покрытия и зазора соответственно; _1/2- интегральная степень черноты поверхности материала; ₀- постоянная Больцмана. Равенство (9) записано в предположении, что теплоперенос в зазоре осуществляется механизмами теплопроводности и излучения.

Приравнивая правые части в (8) и (9), получим

(10)

где

(11)

-коэффициент лучистого теплообмена в зазоре.

Условия сопряжения имеют вид

при r = R₂ (12)

где

(13)

Если теплоизоляционное покрытие отсутствует и _z = 0, условия (12) заменяются условиями идеального теплового контакта

при r = R₂.

Итак, рассматриваемый процесс описывается системой уравнений (5) – (7), (12). Для ее решения воспользуемся конечно-разностным методом.

Введем в рассмотрение две неравномерные координатные сетки, состоящие соответственно из N₁ и N₂ узлов и покрывающие область решения задачи так, как показано на рис. 18. Сетки сдвинуты относительно геометрических границ расплава и изложницы таким образом, что эти границы находятся посредине между соответствующими координатными узлами. Это дает возможность повысить порядок аппроксимации граничных условий.

Для удобства введем безразмерные координаты a = R_S и температуру u_j = (T_j – T₀)/ T₀, j = 1, 2.

В новых безразмерных переменных краевая задача (5)-(7), (12) выглядит следующим образом (штрихи опускаем):

j = 1, 2, (14)

при r = 1, (15)

при r = R₂ / R₃, (16)

при r = 0, (17)

при  = 0, (18)

где

Рис. 18 Неравномерные координатные сетки

Безразмерная температура покрытия определяется из равенства

(19)

где

(20)

Воспользовавшись интегро - интерполяционным методом, получим систему разностных уравнений, аналогичных уравнениям (14):

(21)

которые описывают распределение температур во внутренних узлах расплава (сетка и изложницы (сетка .

Напомним, что уравнения (21) нелинейные, так как коэффициенты , , с зависят от температуры, и на каждом временном слое должны решаться итерационными методами.

Наиболее удобен метод простой итерации.

Вводя обозначения

(22)

получи из (21) следующую систему для определения (s+1)-й итерации температурной сеточной функции на (l + 1)-м временном слое:

(23)

Таким образом, значения коэффициентов a_i, b_i, c_i и d_i вычисляются по значениям температур на предыдущей итерации. В качестве нулевого приближения принимаются значения параметров с предыдущего временного слоя. При s₀ = 0 получаем безитерационную схему, представляющую собой линейный аналог схемы (21). Итерации прекращают, когда разность между последовательными приближениями становится меньше некоторого наперед заданного числа _ит, или когда число итераций превысит определенное заранее максимальное число итераций s₀.

Проведем аппроксимацию граничных условий (15) – (17):

(24)

(25)

(26)

где индекс в круглых скобках указывает на принадлежность сеточной функции расплаву (1) и изложнице (2).

Итак, получили систему (N₁ + N₂) линейных уравнений (23)-(26) для определения (N₁ + N₂) сеточных функций, которую будем решать методом прогонки (в сочетании с итерациями). Этот метод дает возможность решать систему алгебраических уравнений с трехдиагональной ( как в данном случае ) матрицей и устойчив, если выполняются условия преобладания диагональных элементов b_i  a_i + c_i, которые, как легко заметить, следуют из равенств (22).

Реализуем метод прогонки. Предположим, что зависимость между сеточными температурами в i-м и (i +1)-м узлах может быть выражена соотношениями

u_i = x_i+1u_i+1+ y_i+1, (27)

i = 1, 2, …, N₁- 1 на сетке

i = 1, 2, …, N₂- 1 на сетке

где x_i, y_i – некоторые пока неизвестные коэффициенты, которые называются прогоночными.

Затем определим значения первых прогоночных коэффициентов для расплава и изложницы соответственно.

Предположим, что

(28)

и введя обозначения

(29)

получаем

(30)

Таким образом, все прогоночные коэффициенты определены.

Вычисление сеточных температур осуществляется так называемой обратной прогонкой. Из граничного условия (24) с учетом соотношения получаем

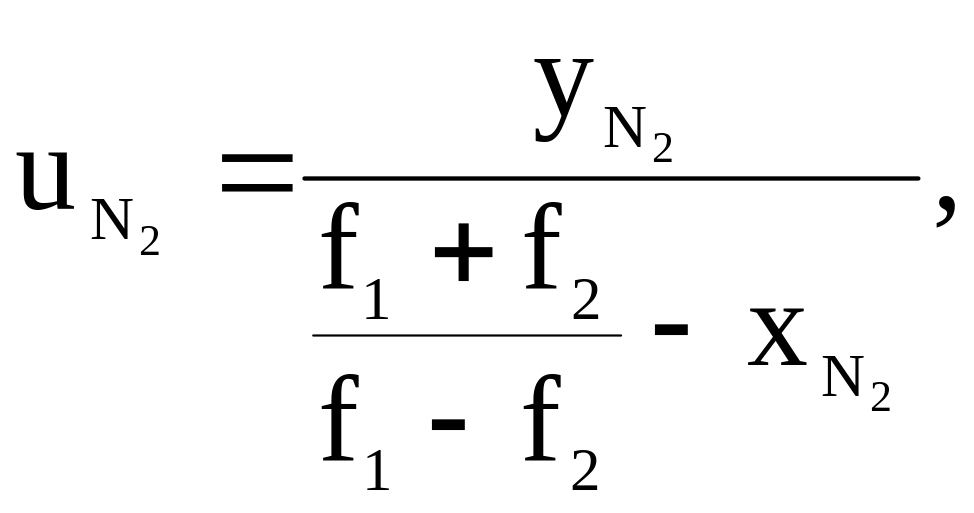(31)

где

Теперь по формулам (27) определяем и Сеточные функции определяются последовательно также из соотношений (27) для расплава. Итак, сеточные функции определены. Далее по известному температурному полю расплава определяется координата фронта затвердевания

u _i  u _ф  u _i-1.

Для нахождения решения на следующем временном слое (следующей итерации) всю описанную выше процедуру повторяют, используя значения теплофизических коэффициентов, рассчитанных по вновь определенному полю температур.

Следует отметить, что уравнение теплопроводности (1) в точке r = 0 имеет особенность, которую необходимо учитывать при построении разностной схемы. Обычно в узлах, близких к точке r = 0, переходят к разностной схеме для уравнения теплопроводности в декартовых координатах

(32)

Изложенный выше алгоритм расчета затвердевания металла реализован в программе TEMPOL. Эта программа позволяет решать сопряженную нелинейную краевую задачу теплопроводности о затвердевании в кокиле плоской или цилиндрической отливки, а также полой цилиндрической отливки, получаемой центробежным литьем, с граничными условиями 3 рода на внутренней поверхности.