Кривина кривої

Означення

Нехай - регулярна крива, що віднесена до натурального параметру, , що віднесена до натурального параметру, тоді з цією кривою пов’язана вектор – функція : .

Дамо параметру деякий приріст позначимо кут: = .

Означення

Границю ( ): ( ) = називають кривиною кривої у точці, що відповідає значенню параметра .

Кривину ще називають швидкістю крутіння векторів.

Можна сказати, чим більша кривина, тим більш кривіша ця крива в деякому околі цієї точки, це якась міра, що виміряє кривизну кривої.

Теорема

Нехай - регулярна крива, що віднесена до натурального параметру, , що віднесена до натурального параметру, тоді ( ) = .

Доведення

Цей трикутник рівнобедрений, довжина його сторін дорівнює 1, проведемо висоту AD, тоді з прямокутних трикутників і ADB знаходимо довжину основи трикутника ABC:

= 2 .

Звідси отримуємо:

= 2 = 2 =

Таким чином,

Відмітимо, що оскільки функція неперервна, коли .

Перейдемо в останній рівності до границі, , вважаючи, що модуль функція неперервна = = 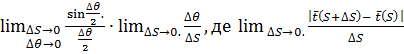, 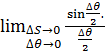= 1, = ( ).

Маємо:

( ).

Крім того, з означення функції = ( ) =| |.

Теорему доведено.

Наслідок (перша формула Френе)

(

Доведення

За означенням вектор – функції випливає

Звідки отримаємо:

(

Наслідок доведено.

Теорема 2

Нехай - регулярна крива. Ця крива тоді і тільки тоді у кожній своїй точці має нульову кривину, коли кожна її точка має деякий окіл, що є образом (в ) деякого інтервалу прямої.

Доведення

Оскільки мова йде про деякі інтервали кривої, то ми можемо перейти до натурального параметру, тобто вважати, що крива задається вектор – функцією . Якщо розглянути окіл, що є образом інтервалу кривої, то з курсу аналітичної геометрії відомо, що цей інтервал задається векторно – параметричним рівнянням прямої: = S + , де направляючий вектор прямої, - вектор, через кінець якого пряма проходить при S = 0, тоді = = , 0.

Таким чином, кривина в усіх точках цього інтервалу є нульова.

Припустимо, що кривина в усіх точках дорівнює нулю. Можемо вважати, що параметр належить натуральним числам. Т оді за теоремою 1: згідно властивостям похідної вектор – функції, сам вектор = . З означення випливає = .

Інтегруючи його, отримаємо:

= S + , а це рівняння є векторно – параметричним рівняння прямої, яке відображає точки - інтервала прямої (числової), на якому розглядається зміна параметру у відповідні точки прямої або площини.

Теорему доведено.

Лема

Нехай - регулярна крива, , цієї ж кривої, що приведена до натурального параметру, = – числова функція, що здійснює приведення до натурального параметру, тоді має місце рівність:

= .

.

Доведення

Перейдемо до натурального параметру за допомогою = функції = , тоді (*) = = = .

Крім того, (**) = ) .

) = ’)’ + ’ = ) .

Таким чином, = ) .

Тоді підставляючи (*) і (**) у векторний добуток, маємо:

= = + = , бо = 0.

Лему доведено.

Твердження

Нехай - регулярна крива при довільній параметризації, , тоді у точці кривої , що відповідає значенню параметра , кривина кривої обчислюється за формулою:

.

Доведення

Нехай = ( ) – функція, що здійснює перехід до натурального параметру. З результату попередньої леми випливає, що

| | = .

Таким чином, нам достатньо довести, що

= = | |.

Дійсно, | | = | | = = = = .