Дотична регулярної кривої

Нехай - регулярна крива, що задана на інтервалі , ія.

Пряма L називається дотичною до кривої у т. Р, якщо .

Теорема

Нехай - регулярна крива, що задана на інтервалі , .

Тоді в кожній своїй т. Р ця крива має дотичну, направляючий вектор якої колінеарний вектору (t), де t - значення параметру, що відповідає т. Р.

Доведення

Нехай - одиничний направляючий вектор прямої L, що проходить через т. Р кривої .Нехай значення параметру, що відповідає т.Q, тоді т.Q P 0. Крім того, довжина відрізку QP : ( )

, =1. За означенням векторного добутку , ( )маємо:

. ( )

За формулою Тейлора для вектор – функцій маємо:

= ( ) + ( ) , де ( ) 0, коли 0.

Тоді з ( ) і ( ) маємо:

, .

Звідси маємо, що:

= .

Поділивши чисельник і знаменник на , маємо:

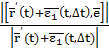= , тоді = = 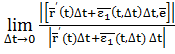= = 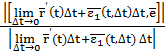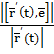, оскільки векторний добуток та довжина вектора (зі скалярного квадрату вектора) є функціями неперервними.

Таким чином, = .

Згідно властивостей векторного добутку і враховуючи, що для регулярної кривої похідна, що в знаменнику , маємо:

=0 = 0, а це означає, що ( )

Таким чином з ( ) що якщо дотична кривої у т. Р, що відповідає значенню параметра , і - її направляючий вектор, то а якщо у якості взяти пряму, що проходить через т. Р і має направляючий вектор , то буде дотичною кривої у т. Р

Теорему доведено.

Наслідок

У кожній точці регулярної кривої існує дотична, при чому єдина.

Рівняння дотичної регулярної кривої

Припустимо, що крива задана своїм параметричним рівнянням:

(*)

Знайдемо рівняння її дотичної в т. Р, що відповідає значенню параметра , тобто: Р ( ).

Згідно попередньої теореми у якості направляючого вектора дотичної в т. Р можна взяти вектор ).

Тоді з курсу аналітичної геометрії, маємо параметричне рівняння дотичної:

де . (1)

Отримаємо пряму і канонічне рівняння дотичної:

. (2)

У випадку плоскої кривої ці рівняння мають вигляд:

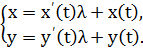де . ( )

. ( )

Припустимо, що крива задана як розв’язок системи функціональних рівнянь:

(3)

Нехай т. лежить на цій кривій. Знайдемо рівняння похідної кривої в т. М.

Згідно теореми про різні способи задання регулярної кривої у деякому околі т. , крива задається своїм параметричним рівнянням (*).

Нехай параметр відповідає т. . Підставляючи (*) в (3) отримаємо тотожності:

Про диференціюємо ці тотожності в т. . Маємо:

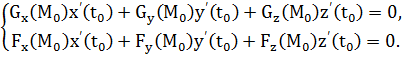(4)

Введемо наступні вектори:

( , ( ), ( ).

Тоді згідно формули для обчислення скалярного добутку через координати векторів, рівняння (4) запишеться наступним чином:

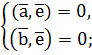
Згідно попередньої теореми є направляючим вектором похідної у т. .

А оскільки , то згідно означення векторного добутку маємо, що .

Таким чином, у якості направляючого вектора дотичної кривої у т. можна взяти вектор .

;

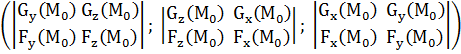Звідки отримаємо канонічне рівняння:

= = .

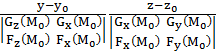У випадку плоскої кривої вона може задаватись неявною функцією G(x, y), при цьому направляючий вектор дотичної в т. з координатами ( ) має вигляд:

( ).

А канонічне рівняння:

= .