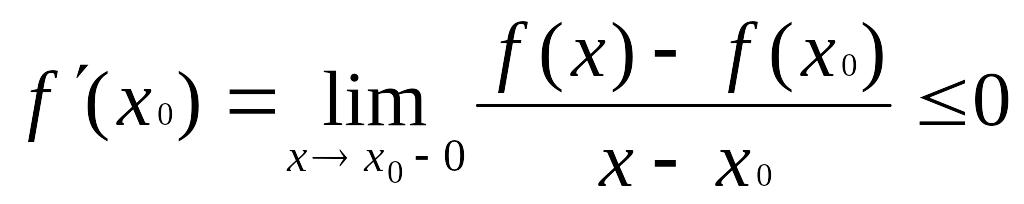§8.Локальный экстремум функции. Теорема Ферма.

Определение 1. Пусть функция определена на множестве и .Говорят, что в точке функция имеет локальный минимум (локальный максимум) , если существует такая окрестность этой точки, что

	(1)
( ),

при этом точку называют точкой локального минимума (локального максимума) функции.

Замечание 1. Если внутренняя точка множества , т.е. если она принадлежит ему вместе с некоторой своей окрестностью то в условии (1) вместо « » можно писать « ».

Замечание 2. Если в точке функция имеет или локальный минимум или локальный максимум , то говорят, что в ней она имеет локальный экстремум ,при этом её саму называют точкой локального экстремума.

Замечание 3. Всякая точка максимума (минимума) фуркции на множестве , т.е. всякая точка , для которой

( ),

иногда называется точкой глобального минимума (глобального максимума) функции на множестве .

Очевидно, что всякая точка глобального экстремума, т.е. глобального максимума или глобального минимума, является также и точкой локального экстремума .

Теорема 1(Ферма). Пусть функция определена на множестве , , при этом - внутренняя точка множества и функция дифференцируема в этой точке .Тогда, если – точка локального экстремума этой функции, то

.

(2)

Д о к а з а т е л ь с т в о. Для определенности будем считать , что ─ точка локального минимума .Тогда такое, что ( ─ внутренняя точка ) и

.

Поэтому

	(3)
.	(4)

Из неравенства (3) , в силу дифференцируемости функции в точке и теоремы о предельном переходе в неравенстве, очевидно следует, что

(5)

а из неравенства (4) , в силу того же, в свою очередь, следует , что

(6)

из неравенств (5) и (6) и вытекает равенство (2) □

§9.Теоремы о среднем для дифференцируемых функций.

Теорема 1 (теорема Ролля). Пусть функция непрерывна на отрезке , дифференцируема на интервале и на концах отрезка принимает равные значения :

(1)

_{Тогда существует такая точка , что}

.

(2)

Замечание 1. Прежде чем доказывать эту теорему отметим , что из геометрических соображений её утверждение очевидно: если выполняется равенство (2) и другие условия теоремы , то найдется такая точка , что в соответствующей точке графика функции касательная к графику параллельна оси абсцисс и ,следовательно тангенс её угла наклона к этой оси равен нулю , что равносильно (2).

Д о к а з а т е л ь с т в о. По первой теореме Вейерштрасса (о непрерывной на отрезке функции) функция ограничена на

отрезке . Следовательно числа

и

конечны.

Если , то очевидно функция является постоянной на отрезке . Тогда в качестве точки , для которой имеет место (2), можно взять любую точку интервала .

Пусть . Тогда выполнено по крайней мере одно из неравенств

(3)

и

(4)

Пусть, например, имеет место последнее из них. По второй теореме

Вейерштрасса о непрерывной на отрезке функции , при этом в силу (4) и , т.е. . По определению числа точка является точкой локального максимума функции (и даже точкой глобального максимума этой функции). Поэтому по теореме Ферма для неё имеет место равенство (2) □

Теорема 2 (Лагранжа). Пусть функция непрерывна на отрезке и дифференцируема на интервале .Тогда найдется такая точка , что

.

(5)

Замечание 2. Терема 2 также имеет простой геометрический смысл. При выполнении ее условий для хорды графика функции с концами в точках и , на графике найдется такая точка , , касательная в которой к графику параллельна этой хорде.

Д о к а з а т е л ь с т в о. Рассмотрим функцию

Она очевидно непрерывна на отрезке , дифференцируема на интервале и на концах отрезка принимает равные значения: .Тогда по теореме Ролля , т.е.

,

а это равносильно равенству (5)□

Замечание 3. Формулу (5) называют формулой конечных приращений Лагранжа. Очевидно, она может быть записана в виде

Для этого достаточно положить в (5) , , a выбрать из условия , т.е. положить . Нетрудно видеть, что формула верна как при , так и при □

_{Теорема 3 (Коши). Пусть функции и непрерывны на отрезке и дифференцируемы на интервале . Тогда} :

(6)

Д о к а з а т е л ь с т в о. Рассмотрим функцию

Она, очевидно, удовлетворяет условию теоремы Ролля, согласно которой , т.е.

что равносильно равенству (6). □