Лекция-1 основы численных методов

§ 2.1. Основные понятия линейной алгебры

Большинство прикладных вычислительных задач, в частности задач расчета строительных конструкций и сооружений, каком-либо этапе сводится к решению задач линейной алгебры. В этом параграфе изложены основные начальные понятия из этой области.

2.1.1. Линейное пространство. Евклидово пространство.

Линейным пространством называется множество элементов любой природы, если выполнены следующие три требования:

I. Имеется правило, посредством которого любым двум элементам и множества ставится в соответствие третий элемент этого множества, называемый суммой элементов и и обозначаемый символом .

II. Имеется правило, посредством которого любому элементу множества и любому вещественному числу ставится в соответствие элемент этого множества, называемый произведением элемента на число и обозначаемый символом .

III. Указанные два правила подчинены следующим восьми аксиомам:

1) (переместительное свойство суммы);

2) (сочетательное свойство суммы);

3) существует нулевой элемент такой, что для любого элемента (особая роль нулевого элемента);

4) для каждого элемента существует противоположный элемент такой, что ;

5) для любого элемента (особая роль числового множителя );

6) (сочетательное относительно числового множителя свойство);

7) (распределительное относительно суммы числовых множителей свойство);

8) (распределительное относительно суммы элементов свойство).

Элементы произвольного линейного пространства принято называть векторами.

В сформулированном определении линейного пространства числа , , … брались из множества вещественных чисел. Поэтому определенное таким образом пространство естественно называть вещественным линейным пространством. При более широком подходе можно брать , , … из множества комплексных чисел. В результате будем иметь понятие комплексного линейного пространства.

Евклидовым пространством (вещественным евклидовым пространством) называется вещественное линейное пространство , если выполнены следующие два требования:

I. Имеется правило, посредством которого любым двум элементам этого пространства и ставится в соответствие вещественное число, называемое скалярным произведением этих элементов и обозначаемое символом .

II. Указанное правило подчинено следующим четырем аксиомам:

1) (переместительное свойство или симметрия);

2) (распределительное свойство);

3) для любого вещественного ;

4) , если ненулевой элемент; , если нулевой элемент.

2.1.2. Арифметическое пространство. Векторы и операции над ними. Линейная зависимость векторов. Базис.

Важнейшим примером линейного пространства является так называемое арифметическое (покомпонентное) пространство. Векторами этого пространства называются упорядоченные совокупности из вещественных (комплексных) чисел, которые называются компонентами вектора. Основным представителем здесь являются вектор-столбец (основной случай; далее вместо термина «вектор-столбец» используется термин «вектор»). Векторы обозначаются одним символом , т.е. имеет место запись:

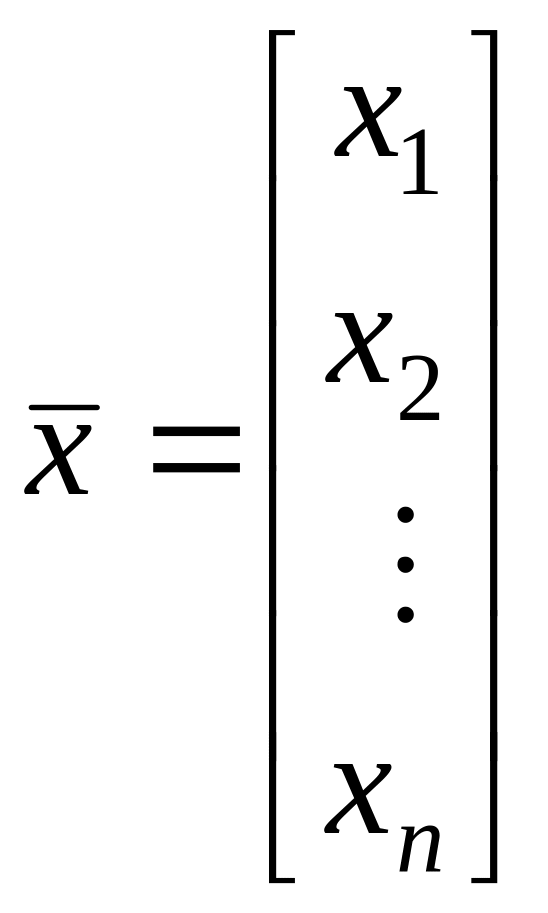– вектор-столбец. (2.1.1)

Число называется -ой компонентой вектора, – номер компоненты.

Само арифметическое пространство в вещественном случае далее будем обозначать , а в комплексном – .

Два вектора арифметического пространства считаются равными в том и только в том случае, если равны их соответствующие компоненты. Действия сложения и умножения на число определяются покомпонентно:

– сложение по правилу

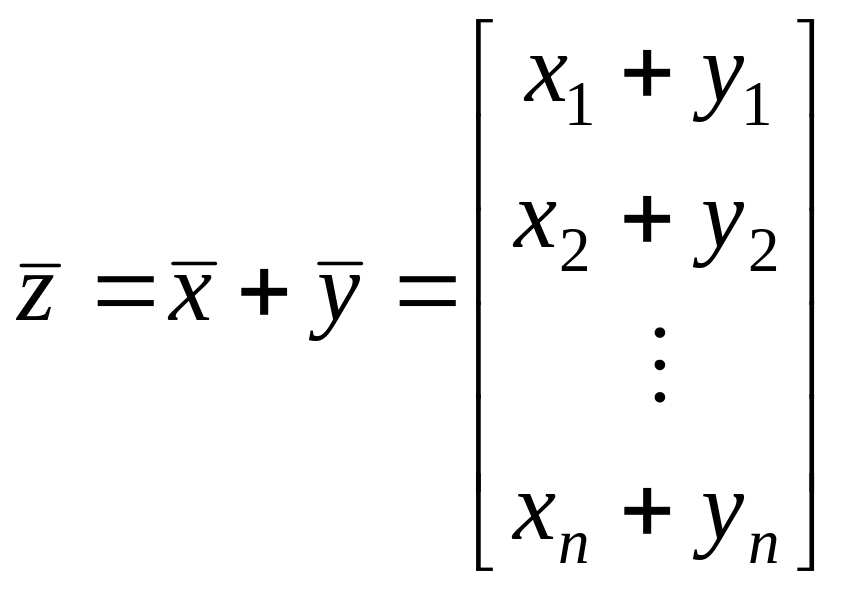; (2.1.2)

– умножение вектора на число по правилу

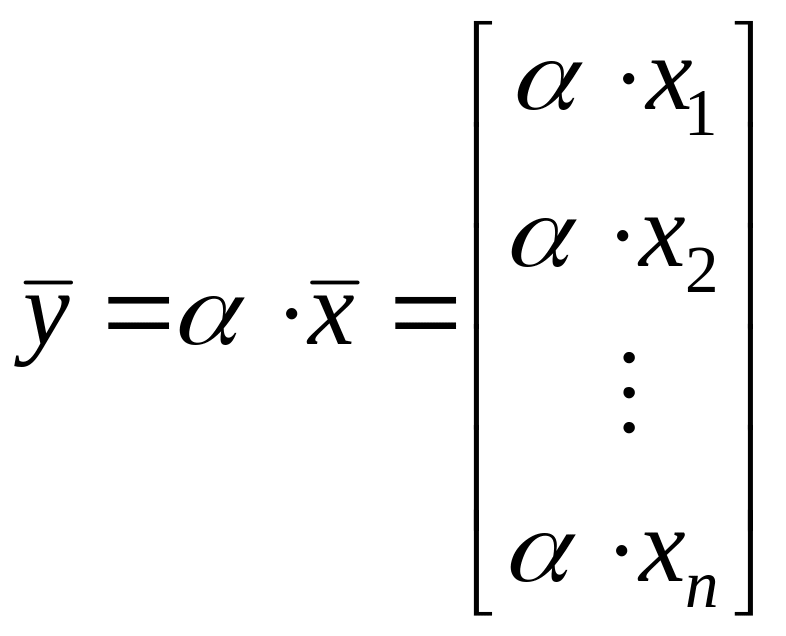. (2.1.3)

Противоположным вектором для вектора является вектор . Роль нулевого вектора играет вектор, все компоненты которого равны нулю, т.е.

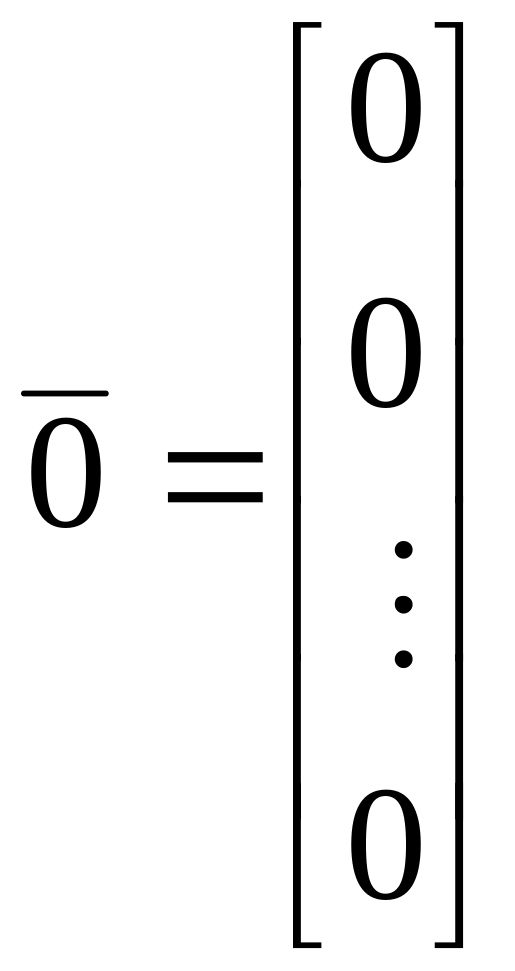– нулевой вектор. (2.1.4)

Арифметическое пространство может быть построено также и на основе вектор-строки:

– вектор-строка, (2.1.5)

где «^T» – знак матричного транспонирования.

Для вектор-строки соответствующие операции определяются аналогично.

Линейной комбинацией векторов , , …, будем называть сумму произведений этих элементов на произвольные вещественные числа, т.е. выражение вида

(2.1.6)

где – произвольные числа.

В частности, на основании (2.1.6) для пары векторов , (при и ) можем определить операцию вычитания векторов:

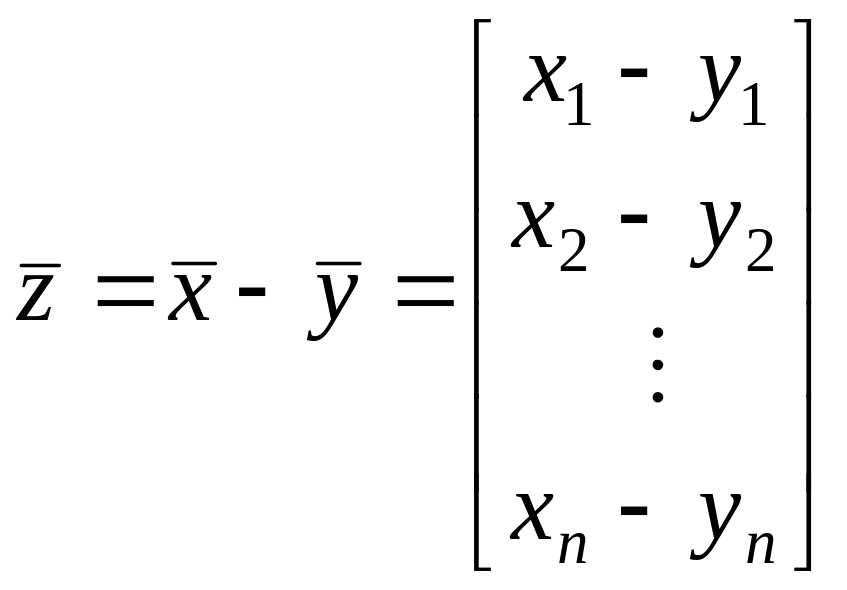. (2.1.7)

Линейно зависимыми векторами , , …, называются векторы, для которых найдутся такие числа , из которых хотя бы одно отлично от нуля, при этом линейная комбинация векторов , , …, с указанными числами является нулевым вектором, т.е.:

. (2.1.8)

Линейно независимыми векторами , , …, называются векторы, если их линейная комбинация (2.1.6) является нулевым вектором лишь при условии .

Сформулируем без доказательства ряд утверждений.

1. Для того, чтобы векторы , , …, были линейно зависимы, необходимо и достаточно, чтобы один из этих элементов являлся линейной комбинацией остальных элементов.

2. Если среди векторов , , …, имеется нулевой вектор, то эти элементы линейно зависимы.

Единичным вектором в называется вектор , i-ая компонента которого равна единице, остальные нули, т.е.

, ; . (2.1.9)

Базисом пространства ( ) называется совокупность линейно независимых векторов , , …, пространства ( ), если для каждого вектора пространства найдутся вещественные (комплексные) числа такие, что справедливо равенство

. (2.1.10)

Например, единичных векторов , , …, образуют базис в .

Равенство (2.1.10) называется разложением вектора по базису , , …, , а числа называются коэффициентами этого разложения. Каждый вектор пространства ( ) может быть разложен по базису , , …, единственным способом, т.е. коэффициенты разложения каждого вектора по базису , , …, определяется однозначно.