Вопрос 17. Формы записи задачи линейного программирования, их эквивалентность и способы преобразования

Модель задачи линейного программирования (ЗЛП) может быть записана в одной из приведенных ниже форм:

1 Общая, или произвольная, форма записи:

при ограничениях:

где c_j, a_ij, b_i — заданные действительные числа.

2 Симметричная, или стандартная, форма записи:

3 Каноническая, или основная, форма записи:

.

Указанные выше три формы записи ЗЛП эквивалентны в том смысле, что каждая из них с помощью несложных преобразований может быть сведена к другой форме.

При необходимости задачу минимизации можно заменить задачей максимизации, и наоборот. Очевидно, что минимальное значение функции F(x) равно максимальному значению функции –F(x), взятому с противоположным знаком, т.е.

min F(x) = – max(–F(x)).

Неравенство типа > путем умножения левых и правых частей на –1 можно превратить в неравенство типа <, и наоборот.

Ограничения-неравенства

преобразуются в ограничения-равенства путем прибавления (вычитания) к левым частям дополнительных (балансовых) неотрицательных переменных x_n+i > 0:

.

В случае необходимости ограничение-равенство

можно записать в виде системы неравенств

Если в ЗЛП какая-то переменная x_k не подчинена условию неотрицательности, ее заменяют разностью двух других неотрицательных переменных х'_k > 0 и х"_k > 0:

x_k= х'_k - х"_k.

Вопрос 18. Двойственность в задачах линейного программирования

С каждой задачей линейного программирования тесно связана другая линейная задача, называемая двойственной; первоначальная задача называется исходной, или прямой.

Каждая из задач двойственной пары фактически является самостоятельной задачей линейного программирования и может быть решена независимо от другой.

Связь исходной и двойственной задач заключается, в частности, в том, что решение одной из них может быть получено непосредственно из решения другой.

Переменные двойственной задачи у_i называют двойственными оценками, или теневыми ценами ресурсов, или объективно обусловленными оценками, или «ценами» ресурсов.

Задача, двойственная к прямой задаче, строится по следующим правилам:

1. упорядочивается запись исходной задачи, т. е. если целевая функция задачи максимизируется, то ограничения-неравенства должны быть вида , если минимизируется, то вида ≥ . Выполнение этих условий достигается умножением соответствующих ограничений на –1;

2. если прямая задача – на максимум целевой функции, то двойственная будет на минимум;

3. число неравенств в системе ограничений одной задачи совпадает с числом переменных в другой задаче;

4. матрица коэффициентов при неизвестных в системе ограничений одной задачи является транспони­рованной к матрице коэффициентов системы ограничений другой

5. коэффициенты при переменных целевой функции одной задачи являются свободными членами ограничений другой;

6. каждому ограничению одной задачи соответствует переменная другой задачи: номер переменной совпадает с номером ограничения.

7. Если на j-ю переменную прямой задачи наложено условие неотрицательно­сти, то j-е ограничение двойственной задачи будет неравенством, в противном случае j-e ограничение будет равенством; аналогично связаны между собой ограни­чения прямой задачи и переменные двойственной. Если функциональное ограничение прямой задачи является равенством, то соответствующая переменная двойственной задачи может принимать как положительные, так и отрицательные значения (т.е. быть любого знака).

Если целевая функция одной из задач неограниченна (например, для задачи на максимум – сверху) то другая задача вообще не имеет решения.

Задача, двойственная по отношению к прямой задаче, составляется согласно правилам, представленным в таблице 1 [1–5].

Таблица 1 – Соответствие двойственных задач ЛП

Исходная (прямая) задача	Двойственная задача
Целевая функция F(x) → max	Целевая функция F ′(x) → min
Константы в правых частях ограничений	Коэффициенты целевой функции
Коэффициенты целевой функции	Константы в правых частях ограничений
j-й столбец коэффициентов в ограничениях	j-я строка коэффициентов в ограничениях
j-я строка коэффициентов в ограничениях	j-й столбец коэффициентов в ограничениях
j-я неотрицательная переменная	j-e неравенство вида ≥
j-я переменная без ограничений в знаке	j-e ограничение вида =
i-e ограничение вида ≤	i-я неотрицательная переменная
i-e ограничение вида =	i-я переменная без ограничений в знаке

Если задачу ЛП рассматривать как задачу об использовании ресурсов (сырья), то параметры задачи имеют следующий смысл. В прямой задаче  – количество единиц j-го продукта; – стоимость единицы j-го продукта; – ресурс j-го продукта. В двойственной задаче теневая цена – стоимость единицы i-го сырья. Стоимость всех ресурсов .

Пример 1. Рассмотрим пример прямой задачи про столы и шкафы (см. вопрос 16).

F = 0,7 ∙ х₁ + 1,3 ∙ х₂  max

0,15∙х₁ + 0,3∙х₂  100

0,25∙х₁ + 0,1∙х₂  50

х₁, х₂ ≥ 0

Прямая задача (ПЗ) на максимум, поэтому двойственная – на минимум.

Запись прямой задачи является упорядоченной, т. е. целевая функция задачи максимизируется, и ограничения-неравенства вида меньше либо равно  .

В ПЗ два ограничения, поэтому в ДЗ – две переменных у_i, .

В ПЗ две переменных, поэтому в ДЗ два ограничения.

Коэффициентами целевой функции ДЗ станут правые части ограничений ПЗ.

F' = 100 y₁ + 50 y₂  min

Матрица коэффициентов при неизвестных в системе ограничений ДЗ получается транспонированием матрицы коэффициентов ПЗ.

Правыми частями ограничений ДЗ станут коэффициенты целевой функции ПЗ.

Так как на переменные прямой задачи наложено условие неотрицательно­сти, то ограничения ДЗ будут неравенствами со знаком больше либо равно ≥ , кроме того, на переменные ДЗ будет наложено условие неотрицательности.

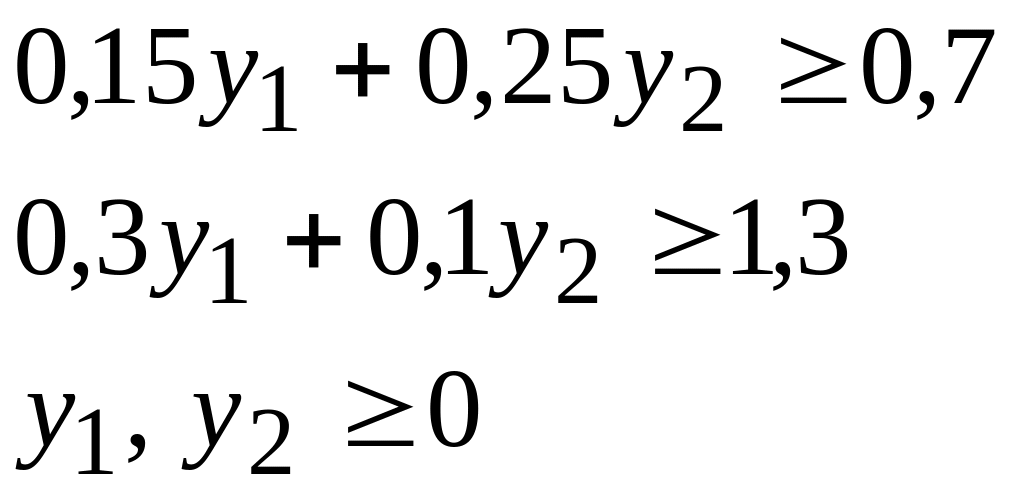
Пример 2.

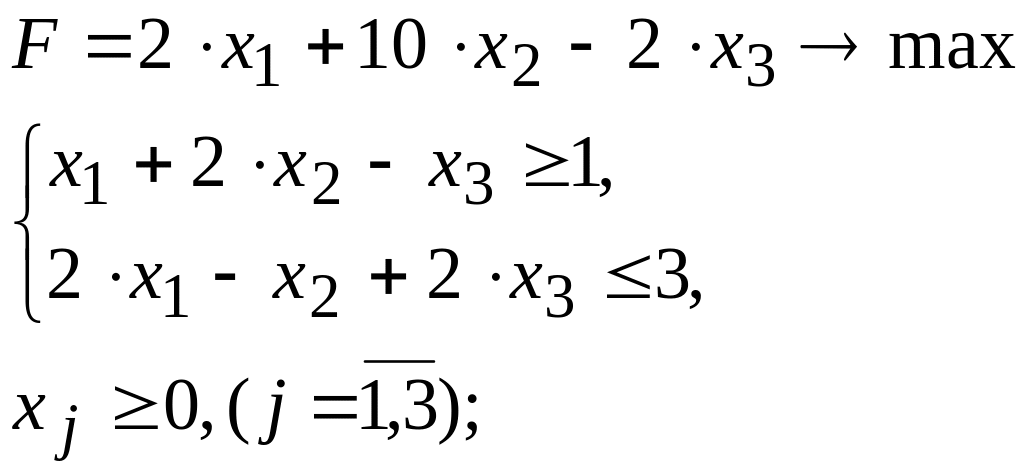
Решение:

Сведем ограничения типа ≥ к ограничениям ≤ умножением на –1.

Двойственная задача является задачей на минимум, а ограничения имеют знаки ≥.

Так на все переменные наложены условия неотрицательности, то в двойственной задаче все ограничения будут являться неравенствами.

Так как ограничений в прямой задаче – два, то двойственная задача будет иметь две переменные, а так как прямая задача содержит три переменные, то двойственная задача будет иметь три ограничения.

Коэффициенты ограничений двойственной задачи получим транспонированием системы ограничений прямой задачи.

Учитывая указанные выше правила, имеем двойственную задачу:

Пример 3.

Решение:

Двойственная задача является задачей на минимум, а ограничения имеют знаки ≥.

Так как на переменные наложены условия неотрицательности, то ограничения двойственной задачи будут ограничениями-неравенствами. Так как ограничения прямой задачи являются равенствами, то на переменные двойственной задачи не накладывается условие неотрицательности.

Так как ограничений в прямой задаче – два, то двойственная задача будет иметь две переменные, а так как прямая задача содержит четыре переменные, то двойственная задача будет иметь четыре ограничения.

Коэффициенты ограничений двойственной задачи получим транспонированием системы ограничений прямой задачи.

В результате получим следующую модель двойственной задачи:

Т.к. ограничения прямой задачи являются равенствами, то соответствующие переменные двойственной задачи могут принимать как положительные, так и отрицательные значения.