Лабораторная работа №1

Лазерный динамический гониометр для поверки и калибровки многогранных призм

Цель работы – аттестация многогранной призмы.

1. Общие положения Описание лабораторной установки

Гониометр динамический ДГ-01Л предназначен для измерений углов между нормалями к плоским отражающим поверхностям призматических мер плоского угла в автоматизированном режиме, имеющих покрытия с коэффициентом отражения не менее 40%.

Схема построения лазерного динамического гониометра (ЛДГ) представлена на рисунок 1.

Рисунок 1 Структурная схема лазерного динамического гониометра: 1 – кольцевой лазер; 2 – поворотная платформа; 3 – привод; 4 – многогранная призма; 5 – нуль-индикатор; 6 – блок электроники; 7 − вычислитель (персональный компьютер)

В составе ЛДГ можно выделить аппаратную часть I и вычислительную часть II. Аппаратная часть обеспечивает получение сигнала с кольцевого лазера (КЛ), формирование интервалов суммирования сигналов с КЛ, передачу информации в вычислительную часть (персональный компьютер). Вычислительная часть осуществляет обработку полученной информации, вывод и хранение результатов обработки. Поворотная платформа 2 приводится в движение приводом 3. На оси вращения платформы закреплены КЛ и многогранная призма (МП) 4. Блок электроники содержит систему управления двигателем, формирователи сигналов, специализированную плату счетчиков, интегрирующую сигнал КЛ в пределах временных интервалов, задаваемых нуль-индикатором (НИ) 5 и передающую данные вычислителю (персональному компьютеру).

КЛ вращается вместе с МП с квазипостоянной частотой. Световой пучок нуль-индикатора (НИ), который установлен на основании гониометра, развертывается в горизонтальной плоскости благодаря отражению от граней вращающейся МП. НИ генерирует импульсы в те моменты времени, когда световой пучок падает по нормали к грани МП.

При вращении КЛ частота выходного сигнала пропорциональна его угловой скорости:

, (1)

где k − масштабный коэффициент КЛ.

В процессе угловых измерений периоды выходного сигнала КЛ интегрируются в пределах интервалов времени, сформированных выходными импульсами НИ. Интегрирование выражения (1) дает число периодов N_i интервале времени 0 ...t_i, в течение которого КЛ поворачивается на угол _i.

, (2)

где t_i − время измерения угла _i.

Интегрирование выражения (1) на угле 2π определяет число периодов выходного сигнала КЛ на полном обороте:

.

Измерение времени формирования импульсов с НИ позволяет проводить вычисление углов МП, используя выражение:

, (3)

где − вертикальная составляющая скорости вращения Земли;

− время формирования импульса НИ, время полного оборота КЛ, соответственно.

С целью увеличения разрешающей способности гониометра в контроллере съема реализована временная интерполяция выходного сигнала КЛ.

Обычно измерение продолжается в течение N оборотов КЛ. В этом случае результатом измерения являются:

среднее значение − ;

среднеквадратическое отклонение − .

Метод кросс-калибровки

В настоящее время известны методы определения погрешности угловой шкалы гониометра. Наиболее известен метод кросс-калибровки применительно к измерениям межгранных углов МП.

Рассмотрим метод кросс-калибровки для определения систематической погрешности ЛДГ при измерении полного угла МП. На рисунке 2 представлено схематическое изображение МП на платформе ЛДГ, на котором показаны нормали идеальной и реальной МП.

Основная задача калибровки МП заключается в определении углов между этими нормалями. Процесс измерения в ЛДГ, как отмечалось ранее, проходит при совместном непрерывном квазипостоянном вращении КЛ и МП.

Рисунок 2 Блок-схема измерений многогранной призмы в методе кросс-калибровки

При совпадении нормали к грани МП и оптической оси нуль-индикатора осуществляется считывание с угловой шкалы КЛ.

Таким образом, результат измерения углов между гранями МП лазерным динамическим гониометром запишется в виде:

, ,

где 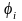− угол между i –ой и первой гранями МП; − угол между нормалями идеальной и реальной МП; − погрешность угловой шкалы, которая характеризует отклонение угловой шкалы КЛ от идеальной (равномерной); N – количество граней МП.

Систематическая погрешность измерения углов МП равна и содержит комбинацию погрешности КЛ и комбинацию погрешности МП.

Процедура кросс-калибровки требует наличия в измерительной системе двух измерительных преобразователей угла, желательно разного типа. Процедура кросс-калибровки заключается в проведении поэтапной калибровки одного преобразователя с помощью другого (обычно в качестве такого преобразователя используют преобразователь с более высокой разрешающей способностью). После каждого этапа калибровки производится разворот корпуса (статора) одного из преобразователей относительно другого на угол 360/n, где n – число этапов кросс-калибровки. В результате получается массив данных, обработка которого позволяет получить систематические составляющие погрешностей обоих преобразователей. Важным фактором при проведении процедуры кросс-калибровки является число n разворотов (или минимальный угол разворота 360/n). Максимальной гармоникой систематической погрешности, которую можно определить с помощью кросс-калибровки, является n/2-ая гармоника.

Для выделения систематической погрешности КЛ необходимо осуществить процедуру кросс-калибровки, которая в данном случае заключается в измерении углов МП, когда она последовательно занимает положения относительно КЛ, которые отличаются на угол 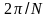. Пусть МП последовательно разворачивается против часовой стрелки на угол . Результат измерений ЛДГ в N положениях МП ( ) имеет вид:

, (4)

где j – номер положения МП, j = 1,2,…,N.

Решая систему уравнений (4) с учетом очевидных соотношени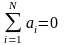й:

и ,

находим

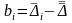, (5)

где , .

Случайная погрешность оценки при независимых измерениях равна: . Следует отметить, что результат измерений ЛДГ содержит кроме оценки матожидания измеряемого угла также среднеквадратическое отклонение результата измерения, которое используем для оценки случайной погрешности .

Пусть в результате измерений ЛДГ имеем отклонение углов МП от их номинальных значений ( ), и дисперсию результатов измерений ( ). В отсутствии внешних возмущающих факторов . Очевидно, что в этом случае:

, .

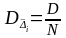При N >5, .

Таким образом, СКО оценки равно:

.

При калибровке МП с помощью ЛДГ нет необходимости проводить измерения в N положениях МП, так как при калибровке МП для устранения погрешности, обусловленной неравномерностью угловой шкалы КЛ на первой гармонике, достаточно провести измерения при ее разворотах на 180^о. Не исключенная систематическая погрешность ( ) при калибровке МП в этом случае будет равна:

,

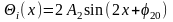где , – амплитуда и начальная фаза 2-ой гармоники.

При калибровке МП в ее 4-ех положениях, отличающихся на 90^о, погрешность неравномерности угловой шкалы ЛДГ устраняется полностью.