Адаптивный алгоритм идентификации

Под адаптивным понимают алгоритм позволяющий уточнять значения идентифицируемых параметров модели по мере получения дополнительной информации о работе объекта.

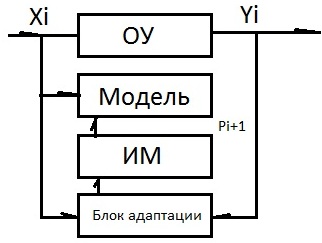
Пусть на i-ом шаге адаптивной идентификации были получены определенные значения параметров. Далее была получена дополнительная информация. Очевидно, что эта информация каким то образом изменяет имеющиеся значения и дает возможность получить параметры P_i+1 .

Этот алгоритм позволяет определить последующие значения параметров, исходя из предыдущих и новой информации. Таким образом, адаптация представляет собой способ получения нового знания путем коррекции старого, на основе новой информации. Если адаптивный метод идентификации реализуется в реальном времени, то его называют еще методом самонастраивающейся модели. Адаптивный алгоритм проще. Его легко программировать и отлаживать.

Схема метода:

ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТОВ ДЛЯ ОПИСАНИЯ ПАРАМЕТРОВ МОДЕЛИ

Планирование экспериментов используется, когда управляемый вход объекта в режиме нормальной эксплуатации во времени, почти не меняется. Поэтому, влияние этого хода не удаётся выяснить без специально спланированных экспериментов.

Имеем зависимость выхода от входа:

Y=F(X;U;P)

X – неуправляемая входная переменная.

U – управляемая.

P – неизвестный параметр. Его надо определить на этом этапе.

В некоторых случаях, планирование экспериментов позволяет определить не только P, но и уточнить структуру модели S. Можно выбрать модель из набора конкурирующих, и тут же определить её параметр. Т. о. планирование экспериментов заключается в таком минимальном изменении входа U, при котором полученная информация Y давала бы возможность наилучшим образом определить значение параметров P.

Критерий планирования определяет эффективность проведенных экспериментов. Обычно в качестве критерия берут минимальные ошибки в оценке параметров P. Ресурсы планирования состоят из выделяемых на эксперимент средств (материальных и временных). Кроме того, к ресурсам относят пределы изменения входа в процессе планирования. Сам эксперимент однозначно определяется в плане; представляет собой перечень состояний входа, которые должны быть реализованы в объекте управления.

Последовательность проведения эксперимента:

Вначале для ОУ выбирают факторы Xi, которые оказывают существенное влияние на выход Y. Определяют области изменения Xi. Все факторы должны быть независимы друг от друга. Затем составляют план эксперимента. Затем, принудительно изменяя Xi, в избранных пределах и сочетаниях, фиксируют значение Y. При постановки задачи, устанавливаются центр и границы варьирования, т. к. значения Xi могут иметь разную физическую природу и размерность. Желательно пользоваться относительными величинами входных переменных.

Xi_max = (Xi_max – Xi_0) / ∆Xi = +1

Xi_min = (Xi_min – Xi_0) / ∆Xi = -1

Xi_max и Xi_min – значения факторов.

∆Xi – интервал варьирования.

Xi_0 – координата центра варьирования.

План проведения эксперимента и методика расчета параметров модели зависит от выбранной структуры модели. Чаще всего это полином:

y = a₀x₀ + a₁x₁ + a₂x₂ + a₁₁x₁² + a₂₂x₂² + a₁₂x₁x₂

Меняем его на следующий: .

Составляем план эксперимента, который устанавливает сколько раз и в какой последовательности надо менять х_i, чтобы при минимальном количестве экспериментов, получить достоверный результат. Эксперимент при котором перебирают все возможные варианты Х называют полно-факторным экспериментом ПФЭ2ⁿ. Таким образом, планирование экспериментов позволяет получить параметры эксперимента, причем на входе может быть несколько переменных. Модель может быть нелинейной и описываться полиномами разных степеней.

Пример:

Необходимо получить модель отражающую зависимость объемной производительности токарного станка от глубины резания и подачи при постоянной скорости.

Принимаем в качестве модели полином следующего вида:

(1)

t=4мм; S=0.7мм/об; =400мм³/мин; =1мм; S=0,1мм/об

Х0	Х1	Х2	Х1Х2	Q0
+1	-1	-1	+1	285
+1	+1	-1	-1	435
+1	-1	+1	-1	350
+1	+1	+1	+1	530

После проведения эксперимента, фиксируют значения Q₀ и определяют параметр модели:

a_i = ( ∑x_i∙y_j ) / 4 = (const)

И полученные значения подставляем в (1).

Из последнего уравнения видно что целевая функция Q не линейна, т. к. есть произведение t∙S. Наиболее значимым фактором является t; S меньше влияет на Q.