2.5. Показательное распределение

Непрерывная случайная величина X называется распределенной по показательному закону, если ее плотность распределения вероятности имеет вид:

где , - параметр распределения.

Функция распределения показательного распределения имеет вид:

Графики функции распределения и функции плотности представлены на рис. 10 и рис. 11, соответственно.

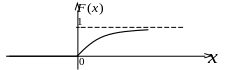
Рис. 10

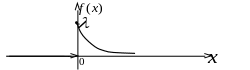
Рис. 11

Числовые характеристики случайной величины, распределенной по показательному закону, вычисляются по формулам:

(16)

К показательному распределению приводят задачи о длительности безаварийной работы различных машин и приборов, оно играет особую роль в теории массового обслуживания и надежности, в страховом деле, демографии и многих других прикладных дисциплинах.

Простейший поток событий

Потоком событий называют последовательность событий, наступающих одно за другим в случайные моменты времени.

Поток событий называется стационарным, если вероятность появления k событий на любом участке времени длительности t не зависит от начала его отсчета.

Поток событий называется ординарным, если вероятность появления на данном участке двух или более событий пренебрежимо мала по сравнению с вероятностью одного события.

Поток событий называется потоком без последствия, если вероятность появления на любом участке времени того или другого числа событий не зависит от того, какое число событий попало на другие не пересекающиеся с данным участки.

Стационарный, ординарный поток событий без последствия называется простейшим (пуассоновским) потоком.

Интенсивностью простейшего потока называют среднее число событий, которые появляются в единицу времени.

Если события образуют простейший поток с интенсивностью , то вероятность появления k событий этого потока за время t определяется по формуле Пуассона:

Длительность промежутка времени T между двумя соседними событиями в простейшем потоке есть непрерывная случайная величина, распределенная по показательному закону с параметром .

Пример 14. Случайная величина X – время безотказной работы прибора распределена по показательному закону. Известно, что часов. Найти вероятность того, что неисправность прибора наступит не ранее, чем через 150 часов.

Решение. Так как часов, то - параметр показательного распределения.

Составим функцию распределения случайной величины X:

Требуется найти .

Найдем сначала:

, тогда

.

Ответ: 0,223.

Пример 15. Среднее число заявок на ремонт, поступающих на диспетчерский пункт в одну минуту, равно 3. Считая поток заявок простейшим, найти вероятность того, что новая заявка поступит ранее, чем через 2 минуты.

Решение. Поскольку поток заявок простейший с интенсивностью , то длительность времени T между двумя неисправностями, есть случайная величина, распределенная по показательному закону с параметром . Требуется найти вероятность .

Составим функцию распределения непрерывной случайной величины T:

Тогда:

Ответ: 0,998.