1.2. Биномиальное распределение
Случайная
величина X
называется биномиально
распределенной
с параметрами n
и p,
если возможные значения
она принимает с вероятностями
,
вычисляемыми по формуле Бернулли:
,
,
где
.
Пример 3. Вероятность попадания в цель при одном выстреле из орудия равна 0,8. Производится три выстрела. Составить закон распределения случайной величины – числа попаданий в цель.
Решение.
Дискретная случайная величина X
– число попаданий в цель – распределена
по биномиальному закону с параметрами
- число независимых испытаний (выстрелов)
и
- вероятность попадания в цель при одном
выстреле и может принимать значения
с вероятностями, вычисленными по формуле
Бернулли:
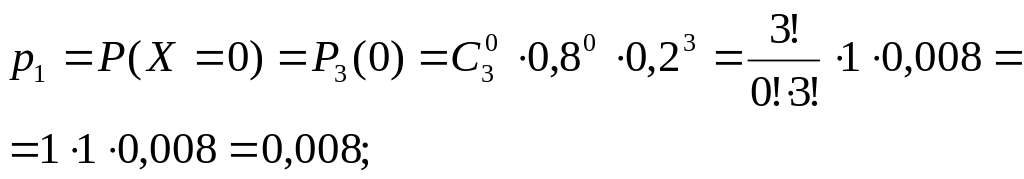
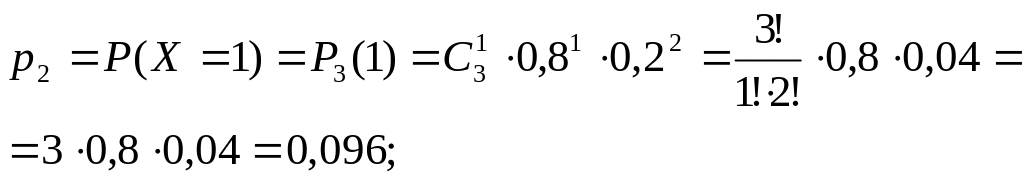
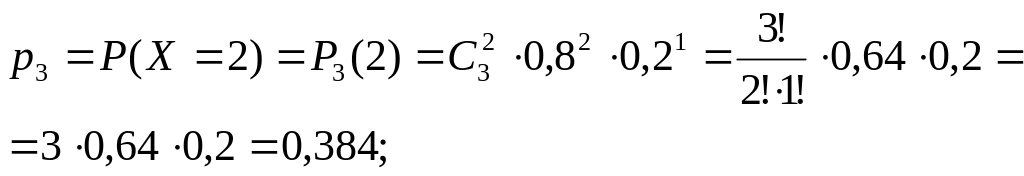
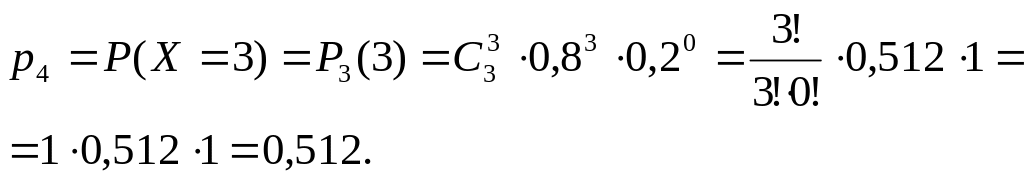
Проверка:
- верно.
Закон распределения случайной величины X имеет вид:
|
0 |
1 |
2 |
3 |
|
0,008 |
0,096 |
0,384 |
0,512 |
1.3. Распределение Пуассона
Случайная
величина X
называется
распределенной
по закону Пуассона
с параметром
,
если она принимает конечное множество
возможных значений
с вероятностями, вычисляемыми по формуле
Пуассона:
,
где
.
Закон распределения случайной величины X имеет вид:
|
0 |
1 |
2 |
3 |
… |
|
|
|
|
|
… |
На
практике случайная величина X
принимает ограниченное число значений
,
так как при достаточно большом
величина
является малой.
1.4. Математические операции над дискретными случайными величинами
Рассмотрим независимые случайные величины X и Y, заданные законами распределения, соответственно:
|
|
|
… |
|
|
|
|
… |
|
|
|
|
… |
|
|
|
|
… |
|
При выполнении математических операций получается новая случайная величина с соответствующими законами распределения:
Произведение случайной величины X на постоянную величину c: cX
|
|
|
… |
|
|
|
|
… |
|
Квадрат случайной величины:
|
|
|
… |
|
|
|
|
… |
|
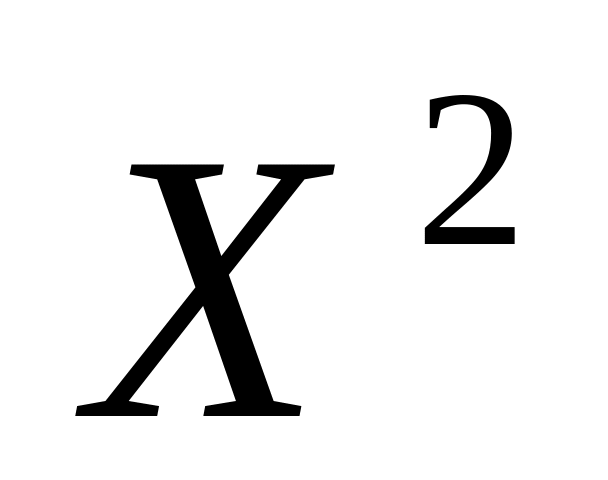
Сумма случайных величин:
|
|
|
... |
|
|
… |
|
|
|
|
... |
|
|
… |
|
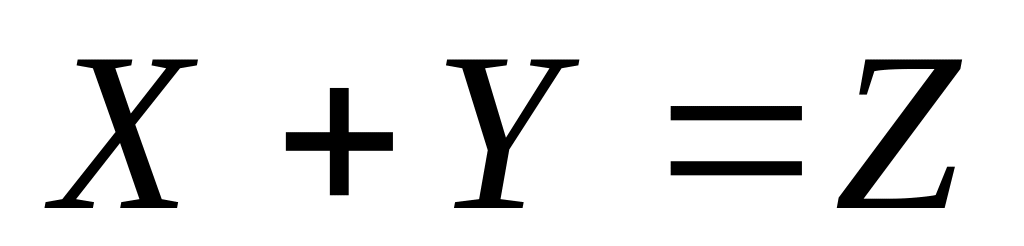
4.
Разность случайных величин:
|
|
|
... |
|
|
… |
|
|
|
|
... |
|
|
… |
|
5.
Произведение случайных величин:
|
|
|
... |
|
|
… |
|
|
|
|
... |
|
|
… |
|
Пример 4. Случайные величины X и Y заданы законами распределения:
|
-1 |
0 |
1 |
|
0,2 |
0,5 |
0,3 |
|
1 |
2 |
|
0,3 |
0,7 |
Составить
закон распределения случайной величины
.
Решение. Для удобства решение оформим в виде таблицы:
|
-1 |
0 |
1 |
|
0,2 |
0,5 |
0,3 |
||
1 |
0,3 |
|
|
|
2 |
0,7 |
|
|
|
В каждой клетке таблицы перечислены все возможные значения случайной величины Z с соответствующими вероятностями. Объединив одинаковые значения, расположим их в порядке возрастания и составим закон распределения искомой случайной величины:
|
0 |
1 |
2 |
3 |
|
0,06 |
0,29 |
0,44 |
0,21 |
