Дискретные и непрерывные случайные величины и их числовые характеристики. Двумерные случайные величины
Дискретными случайными величинами называются случайные величины, принимающие только отдаленные друг от друга значения, которые можно заранее перечислить.
Законом распределения случайной величины называется соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Рядом распределения дискретной случайной величины называют перечень ее возможных значений и соответствующих им вероятностей.
Функцией распределения дискретной случайной величины называют функцию:
,
определяющую для каждого значения аргумента x вероятность того, что случайная величина X примет значение, меньшее этого x.
Свойства функции распределения:
1.
.
2. F(x) – неубывающая функция, т.е.
,
если
.
3. Вероятность того, что случайная величина примет значение, заключенное в интервале [а, b):
.
4. Если возможные значения случайной величины принадлежат интервалу (a, b), то
Биномиальный закон распределения
Биномиально распределенной с параметрами n и p дискретной случайной величиной Х называется величина, характеризующая число появлений события А в n независимых испытаниях Бернулли, в каждом из которых вероятность появления события А равна р. Вероятность того, что Х примет свое значение k задается формулой Бернулли, т.е.
,
где q = 1 – p; k = 0, 1, ..., n.
Закон распределения Пуассона
Распределенной по закону Пуассона с параметром дискретной случайной величиной X называется случайная величина, значения которой – целые неотрицательные числа. Вероятность того, что Х примет свое значение k задается формулой Пуассона, т.е.:
,
где - параметр распределения; k=0, 1, ..., n, ... .
Математическое ожидание дискретной случайной величины
,
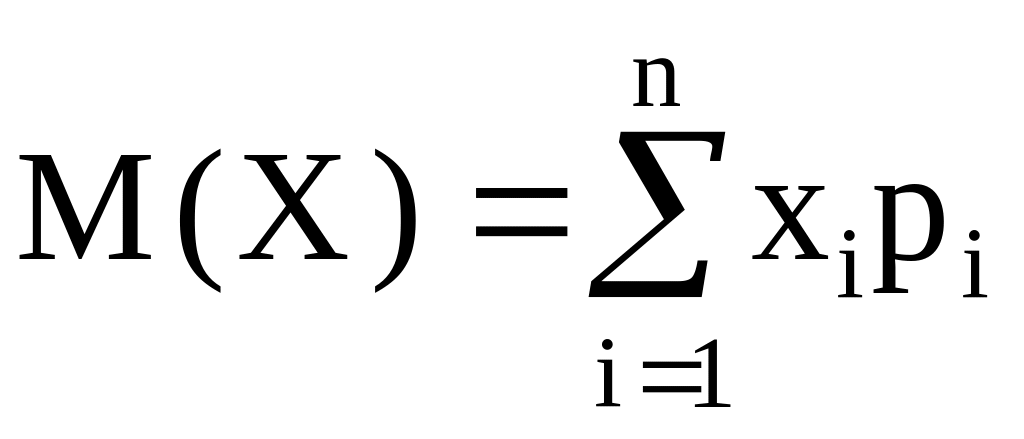где
– значение дискретной случайной
величины;
– вероятности принятия случайной
величиной X значений
.
Если случайная величина принимает счетное множество возможных значений, то:
.
Математическое ожидание биномиально распределенной с параметрами n и p случайной величины:
,
где p - вероятность наступления события.
Дисперсия дискретной случайной величины:
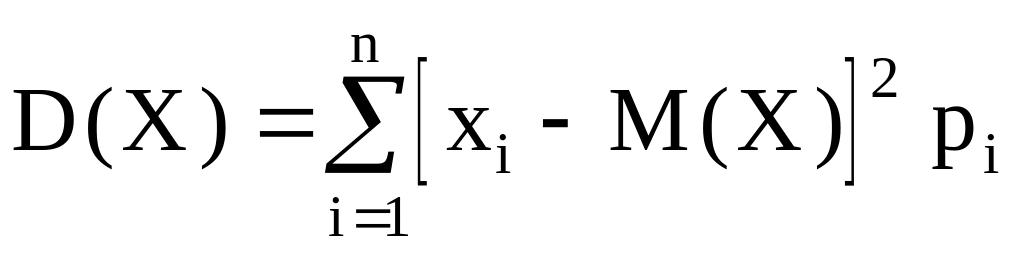
или
.
Дисперсия биномиально распределенной с параметрами n и p случайной величины:
,
где p - вероятность наступления события.
Среднеквадратическое отклонение дискретной случайной величины:
.
Свойства математического ожидания:
1. M(С) = C, где С – постоянная величина.
2. M(СX) = CM(X) , где С – постоянный множитель.
3. M(X+Y) = M(X) + M(Y).
4. M(XY) = M(X) M(Y), где X, Y – независимые случайные величины.
Свойства дисперсии:
1. D(C) = 0, где С – постоянная величина.
2.
,
где С – постоянный множитель.
3. D(X+Y) = D(X) + D(Y), где X, Y – независимые случайные величины.
4. D(C+X) = D(X), где С – постоянная величина.
5. D(XY) = D(X)D(Y) +
,
где X, Y — независимые случайные величины.
Пример. В партии 10% нестандартных деталей. Наудачу отобраны 2 детали. Написать биномиальный закон распределения дискретной случайной величины Х - числа нестандартных деталей среди двух отобранных.
Решение. Дискретная случайная величина Х – число нестандартных деталей среди двух отобранных принимает следующие значения:
х1=0 – все детали стандартны из двух отобранных;
х2=1 – одна из двух отобранных деталей не стандартна;
х3=2 – обе отобранные детали нестандартны. Так как вероятность отбора нестандартной детали p = 0,1 постоянная, то для определения вероятностей в соответствии с биномиальным законом распределения воспользуемся формулой Бернулли:
Pn(k)=
pk qn-k
, где q = 1 – p = 0,9.
P2(0)=
C
(0,1)0
(0,9)2=0,81,
P2(1)=C
0,1 0,9=0,18,
P2(2)=C
(0,1)2(0,9)0=0,01.
Проверяем условие
нормировки 
=1.
Имеем, что 0,81+0,18+0,01=1.
Искомый биномиальный закон распределения дискретной случайной величины Х имеет вид:
|
х |
0 |
1 |
2 |
|
p |
0,81 |
0,18 |
0,01 |
По формуле:
.
Тот же результат можно было получить, используя формулу
для нахождения
математического ожидания биномиально
распределенной дискретной случайной
величины X.
n = 2 – число испытаний;
p = 0,1 – вероятность успеха в каждом испытании;
M(X) = 2 0,1 = 0,2.
Дисперсию найдем по формуле:
.
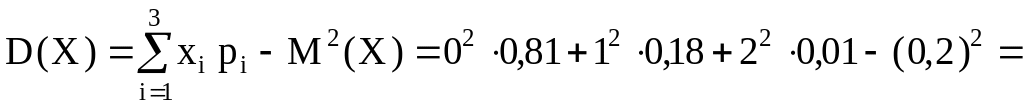
По формуле для дисперсии биномиального закона:
.
Пример. Дискретные случайные величины X и Y независимы и заданы распределениями:
X |
0 |
1 |
|
|
Y |
1 |
2 |
p |
0,4 |
0,6 |
|
|
p |
0,2 |
0,8 |
Найти распределение случайной величины Z = X + Y.
Решение. Найти закон распределения дискретной случайной величины, значит перечислить все ее возможные значения и рассчитать вероятности, с которыми она эти значения принимает. Значения случайной величины Z получаются путем сложения всех возможных попарных комбинаций значений случайных величин Х и Y.
0 + 1 = 1 0 + 2 = 2 1 + 1 = 2 1 + 2 = 3.
Таким образом, Z принимает три возможных значения: 1, 2 и 3. Найдем вероятности принятия величиной Z этих значений.
Так как Z принимает свое значение 1, тогда и только тогда, когда Х принимает значение 0, а Y – значение 1, то случайное событие «Z = 1» является произведением независимых (из-за независимости Х и Y по условию) случайных событий «Х = 0» и «Y = 1». Используя теорему умножения вероятностей независимых событий имеем:
P(Z=1)=P{(X=0)(Y=1)}=P(X=0)P(Y=1)=0,4
0,2=0,08=
.
Так как Z принимает свое значение 2 либо когда X=0, а Y=2, либо когда X=1, а Y=1, причем одновременно это происходить не может, то событие «Z=2» – является суммой несовместных событий (X=0)(Y=2) и (X=1)(Y=1), и его вероятность можно найти с помощью теоремы сложения вероятностей несовместных событий:
P(Z=2)=P{(X=0)(Y=2)+(X=1)(Y=1)}=P{(X=0)(Y=2)}+P{(X=1)(Y=1)}=
=P(X=0)P(Y=2)+P(X=1)P(Y=1)=0,4
0,8+0,6
0,2=0,32+0,12=0,44=
.
Рассуждая аналогично, найдем:
P(Z=3)=P{(X=1)(Y=2)}=P(X=1)P(Y=2)=0,6
0,8=0,48=
.
Проверим выполнение условия нормировки: =0,08+0,44+0,48=1.
Таким образом, искомый ряд распределения имеет вид:
Z |
0 |
1 |
2 |
p |
0,08 |
0,44 |
0,48 |
Непрерывными случайными величинами называются случайные величины, возможные значения которых непрерывно заполняют некоторый промежуток.
Функцией распределения непрерывной случайной величины называют функцию F(x), определяемую также как и функция распределения дискретной случайной величины, т.е.
F(x) = P(X < x).
Плотностью распределения непрерывной случайной величины называется первая производная от функции распределения, т.е.:
,
при этом функция F(x) непрерывно дифференцируемая функция для непрерывных случайных величин.
Свойства плотности распределения:
1. Плотность распределения неотрицательная функция, т.е.
.
2. Условие нормировки:
.
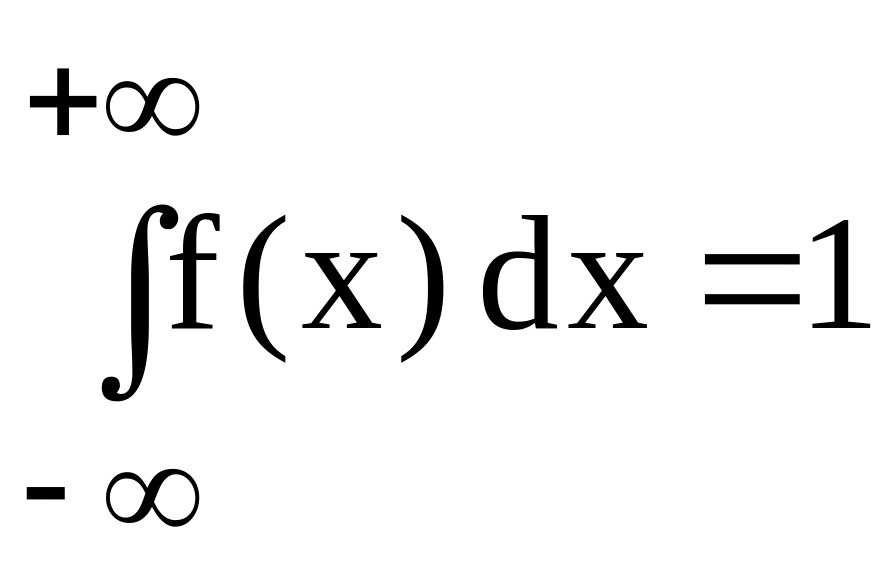3. Вероятность попадания непрерывной случайной величины в заданный интервал (а, b) определяется формулой:
.
4. Через известную плотность распределения непрерывной случайной величины можно найти ее функцию распределения по формуле:
.
Математическое ожидание непрерывной случайной величины:
.
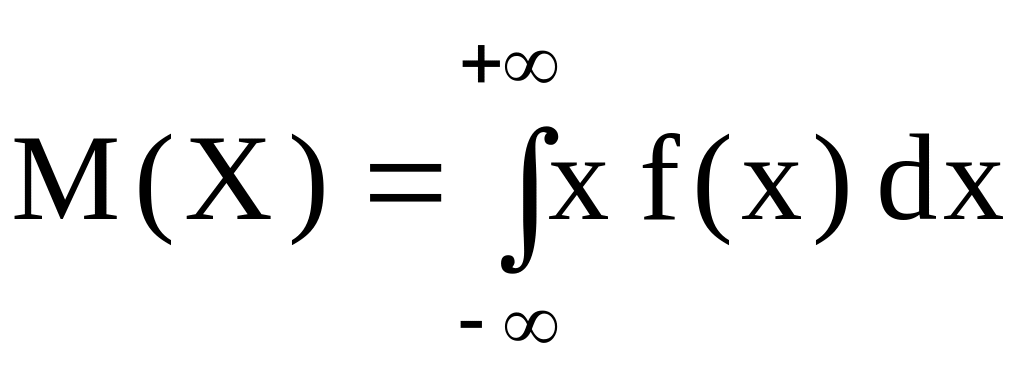Дисперсия непрерывной случайной величины:
или
.
Примечание. Свойства математического ожидания и дисперсии непрерывной случайной величины совпадают со свойствами этих характеристик для дискретных случайных величин.
Пример. Случайная величина X задана плотностью распределения:
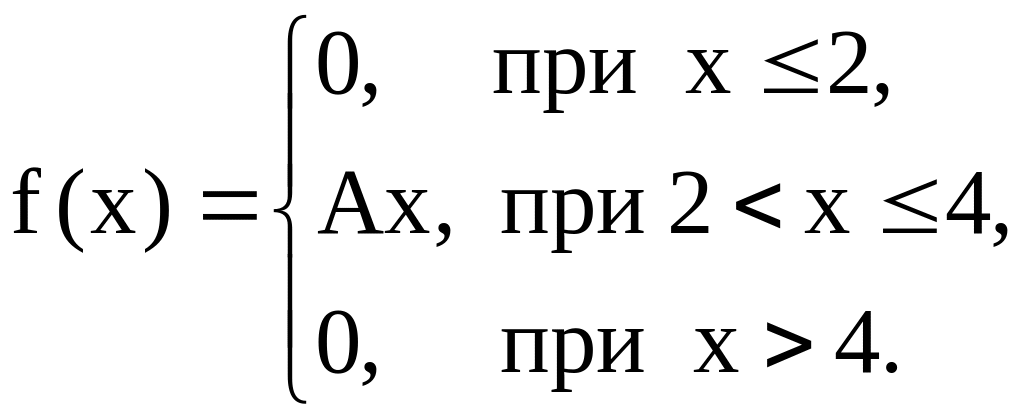
Найти:
1.Коэффициент А, при котором f(x) будет плотностью распределения.
2. Функцию распределения F(x).
3. Вероятность того, что в результате испытания X примет значение
а) меньше 0,2; б) меньше 3.
4. Найти математическое ожидание.
5. Найти дисперсию.
Решение:
1.
Так как по условию
нормировки
,
вычислим А из этого соотношения:
.
Откуда
.
2. Функция распределения непрерывной случайной величины X при известной плотности распределения f(x) определяется из формулы:
.
Данная подынтегральная функция принимает три различных вида на промежутке от - до .
Рассмотрим отдельно каждую ситуацию:
а) при
:
;
б) при
:
;
в) при
:
.
Таким образом:
3. По определению:
,
тогда
.
.
4. Математическое ожидание непрерывной случайной величины X ищем по формуле:
.
5. Дисперсию X ищем по формуле:
.
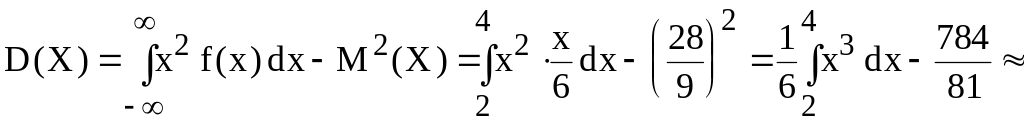
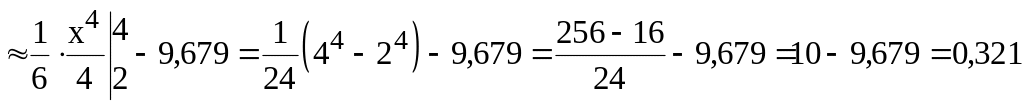