Размещения без повторений

Решим задачу: имеется множество Х, состоящее из m элементов (m-множество). Сколько векторов размерности k можно составить из элементов этого множества, если координаты вектора должны быть различными (не должны повторяться).

Число таких векторов (размещений без повторений из m элементов по k) будем обозначать . Будем рассуждать так: на первое место – имеем n претендентов. После того, как оно заполнено, на второе остается n–1 претендент, на третье – n–2 претендента и т. д.

На k-ое место имеется n – (k – 1) кандидат (т. к. после того, как из m предложенных элементов уже выбрали k - 1, то остался n – (k – 1) =  n – k + 1 претендент на k-ое место). Применяя правило произведения, находим:

.

Умножив числитель и знаменатель на (n–k) . . . 3 2 1, получим окончательный вид формулы:

.

Пример. Сколько слов длины 4 можно составить из 33 букв русского алфавита, при условии, что все буквы различны.

.

Размещения с повторениями

Множества , из элементов, из которых составляются вектора, в правиле произведения могут иметь общие элементы. В частности, все они могут совпадать с одним и тем же множеством Х, содержащим m элементов.

Вектора длины k, составленные из элементов m - множества Х называют размещениями с повторениями (словами длины k в алфавите Х), а их число обозначают .

Из правила произведения сразу вытекает, что

k раз

Пример. Сколько слов длины 6 можно составить из 26 букв английского алфавита?

.

Перестановки без повторений

Решим задачу: сколькими способами можно переставить между собой (поменять местами) сразу все m элементов множества Х?

Число - перестановок без повторений из n элементов – это число способов, сколькими по n местам можно расставить n элементов. Оно легко получается из формулы для размещений без повторений при условии, что размерность создаваемых векторов k равна количеству элементов всего множества n:

.

0! по определению равен 1.

Сочетания без повторений

Решим задачу: сколькими способами из множества можно составить всевозможные подмножества по k элементов каждое?

Число таких подмножеств будем называть числом сочетаний без повторений из m элементов по k и обозначать . Решить ее проще всего тоже исходя из понятия вектора. Если бы мы искали число упорядоченных k - подмножеств без повторений, составленных из множества Х в m элементов, то оно было бы равно

.

Но нас не интересует порядок элементов, выбранный в вектор длины k, а интересует лишь состав. Тогда среди различных векторов k! штук имеют одинаковые компоненты и отличаются лишь их порядком. Таким образом, сочетаний будет в k! раз меньше, чем размещений

.

Число сочетаний без повторений обладает следующими свойствами:

; ;

; ;

.

Удобно, также помнить, что .

Пример.

Из 1, 2, 3, 4 упорядоченных пар можно составить .

12 13 14 23 24 34

21 31 41 32 42 43

При таком расположении заметно, что эти пары можно составить, выбрав сначала в пару какие-то 2 элемента, а затем составить все возможные векторы, переставив данный состав 2! различными способами. Значит, если считать пары, отличающиеся только составом, то их будет в 2! раз меньше, чем .

Пример. Сколько существует различных способов заполнения карточек “Спортлото” 6 из 49? Нам надо выбрать неупорядоченные подмножества размерности k = 6 из множества Х, n= 49.

.

ЗАДАЧИ

1. Определить, обладает ли следующая группа событий свойствами группы случаев:

1. Испытание состоит в бросании 2х монет.

А - выпал хотя бы один герб;

А - выпала хотя бы одна решка.

2. Испытание состоит в 2х выстрелах по мишени.

А - ни одного попадания;

А - ровно одно попадание;

А - ровно два попадания.

3. Испытание состоит в бросании игральной кости.

А - выпало нечетное число очков;

А - выпало четное число очков.

4. Испытание состоит в бросании 3х монет.

А - не выпало гербов;

А - выпал один герб;

А - выпало два герба;

А - выпало 3 герба.

5. Испытание состоит в извлечении 2х карт из колоды.

А - выпали две черные карты;

А - выпали две красные карты.

6. Испытание состоит в бросании игральной кости.

А - выпало не более 2х очков;

А - выпало больше 2х и меньше 5и очков;

А - выпало больше 4х очков.

7. Испытание состоит в бросании 3х монет

А - выпало два герба;

А - выпало две решки.

8. Испытание состоит в извлечении 2х карт из колоды.

А - выпали две черные карты;

А - выпала дама;

А - выпал туз.

2. Среди студентов, собравшихся на лекцию по ТВ, выбирают наудачу одного. Событие А = выбран юноша; В =не курит; С =живет в общежитии.

а) Описать событие .

б) При каком условии будет иметь место тождество АВС = А?

в) Когда будет справедливо соотношение ?

г) Может ли быть верным равенство , если все юноши курят?

2. Мишень состоит из 10 кругов, ограниченных концентрическими окружностями с радиусом , причем 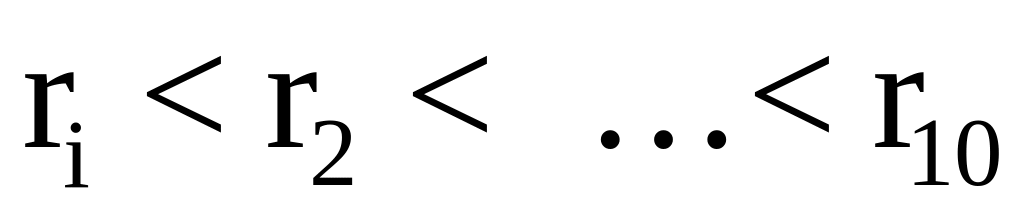. Пусть событие попадание в круг радиуса . Что означают события: ; ; ?

3. Брошены две монеты. Рассматриваются события:

А – выпал «герб» на первой монете;

В – выпала «решка» на первой монете;

С – выпал «герб» на второй монете;

D – выпала «решка» на второй монете;

E – выпал хотя бы один «герб»;

F – выпала хотя бы одна «решка»;

G – выпали два «герба»;

H – выпал ровно один «герб»;

I – не выпало «гербов».

Какими событиями этого списка являются события:

а) А+C; б) АС; в) B+D; г) BD; д) A+E; е) AE; ж) В+F; з) DF; и) AD+BC.

2. Пусть А, В, С  три произвольных события. Записать выражения для событий, состоящих в том, что из событий А, В, С:

а) произошло только А;

б) произошло А и В, но С не произошло;

в) все три события произошли;

г) произошло, по крайней мере, одно из этих событий;

д) произошло, по крайней мере, два события;

е) произошло одно и только одно событие;

ж) произошло два и только два события;

з) ни одно событие не произошло;

и) произошло не более двух событий.

2. В отделе научно-исследовательского института работают несколько человек, причем каждый из них знает хотя бы один иностранный язык. 6 человек из них знают английский, 6 – немецкий, 7 – французский, 4 – английский и немецкий, 2 – английский и французский, 3 – немецкий и французский, 1 человек знает все три языка. Сколько человек работает в отделе? Сколько из них знает только английский язык? Сколько человек знает только один язык?

3. Староста одного класса дал следующие сведения об учащихся: ”В классе учатся 45 школьников, в том числе 25 мальчиков. 30 школьников учатся на хорошо и отлично, в том числе 16 мальчиков. Спортом занимаются 28 учеников, в том числе 18 мальчиков и 17 учеников, учащихся на хорошо и отлично. 15 мальчиков учатся на хорошо и отлично и занимаются спортом.”

Докажите, что в этих сведениях есть ошибка.

2. Сколько чисел среде первых 100 натуральных чисел не делятся ни на 2, ни на 3, ни на 5, ни на 7?

3. На железнодорожной станции имеется 10 путей. Сколькими способами можно расставить на них 3 состава?

4. Десять человек случайным образом рассаживаются за круглый стол. Сколькими способами это можно сделать? Сколькими способами это можно сделать так, что бы два определенных человека А и В оказались сидящими рядом? Что бы три определенных человека А, В и С оказались сидящими рядом?

5. Служащий банка утратил 5-значный код одного из сейфов, состоящий из различных цифр. Сколько вариантов он должен перепробовать, чтобы открыть сейф?

6. Слово составлено из карточек, на каждой из которых написана одна буква. Карточки смешивают и вынимают без возврата по одной. Сколькими способами это можно сделать? Сколькими способами это можно сделать так, чтобы карточки с буквами располагались в порядке следования букв заданного слова: а) «событие»; б) «статистика».

7. На карточках написаны буквы: А, Е, У, У, К, К, К, Р. Карточки перемешаны и разложены в ряд. Какова вероятность, что получится слово “кукареку”.

8. Монета брошена дважды. Сколькими способами это можно сделать? Сколькими способами это можно сделать так, что хотя бы один раз появиться герб.

9. Монета брошена три раза. Сколькими способами это можно сделать? Сколькими способами это можно сделать так:

1. что хотя бы один раз появиться герб;

2. что герб появится только один раз;

3. что решка появится ровно два раза.

16. Из 30 букв алфавита составлено слово длины 6. Сколькими способами это можно сделать? Сколькими способами это можно сделать так, чтобы:

1. в слове была ровно одна буква А;

2. в слове было ровно две буквы А;

3. в слове было ровно 5 букв А;

4. в слове была хотя бы одна буква А.

17. Четверо студентов сдали экзамены. Сколькими способами им могут быть поставлены отметки, если известно, что никто из них не получил неудовлетворительной отметки?

18. Имеется три волчка с 6, 8 и 10 гранями соответственно. Сколькими различными способами они могут упасть? Сколько способов выпадения, если, по крайней мере, два волчка упали на сторону, помеченную “1”?

19. Сколько чисел меньших миллиона можно написать с помощью цифр:

а) 9,8,7;

б) 9,8,0 (цифра “0” не должна быть первой)?

17. Во скольких десятизначных числах сумма цифр равна 3 (первая цифра отлична от нуля)?

18. Сколько можно составить различных пятизначных чисел, делящихся на 25 и не содержащих цифры “0”, если каждая цифра в записи числа может встречаться несколько раз?

19. Сколькими способами среди первых 100 натуральных чисел можно выбрать двузначное число, делящееся:

а) на 8;

б) на 8 и на 3;

в) на 2 , 4 и 6.

17. Монета бросается до тех пор, пока “герб” или “решка” не появится во второй раз. Сколько существует различных результатов данного эксперимента?

18. На карточках разрезной азбуки написано слово “Абакан”. Сколькими способами можно сложить эти карточки случайным образом так, чтобы согласные буквы шли в алфавитном порядке ?

19. У переплетчика 12 различных книг и три цвета переплетной бумаги: красный, зеленый и синий. Сколькими способами он может переплести книги так, чтобы:

1. все книги были переплетены в один цвет;

2. все книги, кроме одной были переплетены в красный цвет, а одна в синий;

3. все книги, кроме одной были переплетены в синий цвет;

4. все книги были переплетены в красный или синий цветa;

5. все книги были переплетены в красный и синий цвета;

6. все книги были переплетены в два каких-нибудь цвета;

7. в каждый цвет была переплетена хотя бы одна книга.

26. Во скольких десятизначных числах сумма цифр равна 5 (первая цифра отлична от нуля)?

27. 10 спортсменов выступают на соревнованиях по спортивной гимнастике. После их выступления трое судей, не сговариваясь, располагают их по 10 местам, согласно месту, которое, по мнению каждого судьи, спортсмен занял. Таким образом, получается три списка спортсменов. Первый приз будет присужден тому, кого назвали первым хотя бы двое из судей. Если этого не произойдет, то судейство считается не состоявшимся и приз не присуждается никому. В какой доле случаев приз будет получен?

28. Куб, все грани которого окрашены, распилен на 1000 кубиков одинакового размера, которые затем тщательно перемешаны. Сколько среди этих кубиков имеют окрашенных граней: а) одну; б) две; в) три: г) ни одной.

29. Человек забыл последнюю цифру телефонного номера. Сколькими способами он может сделать набор, для того чтобы попасть в нужное место не более, чем с третьего раза?

30. Из тщательно перемешанного полного набора домино в 28 костей наудачу извлечена одна кость. Сколькими способами можно приставить к первой наудачу извлеченную вторую кость можно, если первая кость была:

а) дублем;

б) не дублем.

26. Тридцать пять учащихся класса по итогам года имели “5” по

математике – 14 человек;

физике – 15 человек;

химии – 18 человек;

математике и физике – 7 человек;

математике и химии – 9 человек;

физике и химии – 6 человек;

по всем трем предметам – 14 человек;

Сколько учеников данного класса

1. не имеет “5” по указанным предметам;

2. имеет “5” только по математике;

3. имеет “5” не менее, чем по 2-м предметам.

32. В барабане револьвера 7 гнезд. В пяти из них – патроны, а остальные пусты. Барабан приводится во вращение, в результате чего, напротив ствола случайным образом оказывается одно из гнезд. Затем нажимается курок. Если гнездо пустое – выстрела не произойдет, если в нем патрон – выстрел не произойдет. Сколькими способами можно раскрутить барабан 2 раза так, что:

1. выстрелов не будет;

2. первый выстрел будет, а второго нет;

3. первого выстрела не будет, а второй будет;

4. произойдут оба выстрела.

33. Сколько слов можно получить переставляя буквы слова “парабола”, “метаморфоза”, “обороноспособность”?

34. Сколькими способами можно расставить на первой горизонтали шахматной доски короля, ферзя, две ладьи, двух слонов и двух коней? Каким будет ответ, если Фигур будет меньше 8, например, 3 пешки и две ладьи?

35. У мамы было 2 одинаковых яблока, 3 одинаковые груши и 4 одинаковых апельсина. Каждый день она давала своему ребенку по одному фрукту. Сколькими способами это возможно сделать?

36. Для премии на математической олимпиаде выделено 3 экземпляра одной книги, 4 экземпляра другой и 8 экземпляров третьей. Сколькими способами могут быть распределены эти книги между 30 участниками, если каждому вручается не более одной книги?

37. Найдите сумму четырехзначных чисел, получаемых при всевозможных перестановках цифр 1, 1, 4, 4. То же самое для цифр 0, 0, 4, 4.

38. Сколькими способами можно переставить буквы слова “огород”, чтобы три буквы “о” не шли подряд?

39. Сколькими способами можно переставить буквы слова “обороноспособность”, чтобы две буквы “б” не шли подряд?

КЛАССИЧЕСКОЕ И ГЕОМЕТРИЧЕСКОЕ

ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ

Классическое определение вероятности

Если пространство элементарных исходов конечно и его исходы равновозможны, то вероятность события А Р(A) находится как отношение числа благоприятствующих этому событию исходов m к общему числу всех исходов эксперимента n, т.е.:

Р(A) = .

Геометрическое определение вероятности

Геометрическая вероятность используется в случае, когда число равновозможных исходов бесконечно. Геометрической вероятностью, характеризующей вероятность появления случайной точки внутри некоторой области, называется отношение размера этой области к размеру всей области, в которой может появляться данная точка

, где

Р_d - вероятность попадания случайной точки в область S_d;

S - общая область, где может появляться случайная точка.

Пример. Выпущено 100 лотерейных билетов, причем установлены призы, из которых 8 по 1 руб., 2- по 5 руб. и 1-10 руб. Найти вероятность того, что купленный билет выиграл: а) 5 рублей; б) не более 5 рублей.

Решение: а) Для определения искомой вероятности используем формулу классического определения вероятности Р(A)= . Определим общее число исходов n. Оно равно числу выпущенных билетов-100. Определим благоприятное число исходов m. Оно равно числу лотерейных билетов с выигрышем в 5 рублей, т.е. 2. Тогда искомая вероятность равна : Р(А)= = =0,02.

б) Условие выигрыш “не более 5 рублей” означает, что купленный билет должен иметь либо выигрыш, равный 1 рублю (таких билетов 8), либо выигрыш, равный 5 рублям (таких билетов 2).В данном случае общее число исходов, как и в пункте а) равно 100, а число благоприятных исходов равно 10=8+2. Тогда искомая вероятность равна: Р(А)= = =0,1.

Пример. В цехе работают шесть мужчин и четыре женщины. По табельным номерам наудачу отобраны семь человек. Найти вероятность того, что среди отобранных лиц окажутся три женщины.

Решение. Для решения указанной задачи воспользуемся классическим определением вероятности Р(A)= , где А - событие, состоящее в том , что отобраны по табельным номерам три женщины и четверо мужчин; m- число исходов, благоприятствующих появлению событию А; n- общее число исходов. Общее число возможных исходов испытания равно числу способов, которыми можно отобрать семь человек из десяти. Число способов определяется по выражению: .

Число исходов, благоприятствующих появлению события А, определяется числом способов, которым можно отобрать трех женщин из четырех, т.е. и четырех мужчин из шести, т.е. . Следовательно, число исходов, благоприятствующих появлению события А: m= .

Искомая вероятность:

Р(A)= = = =0,5.

Пример. В квадрат со сторонами равными а наудачу бросается точка. Определить вероятность того, что точка попадет внутрь вписанного в квадрат круга. Данная задача решается с использованием формулы геометрического определения вероятности. Мерой пространства элементарных событий является площадь квадрата . Площадь круга - мера события А. . Тогда искомая вероятность будет определяться по формуле .

ЗАДАЧИ

40. Лотерея состоит из 1000 билетов, среди них 150 выигрышных. Наугад вынимается 1 билет из 1000. Чему равна вероятность того, что этот билет выигрышный?

41. Студент знает ответы на 20 вопросов из 30. Какова вероятность того, что он вытащит на экзамене известный ему вопрос?

42. В студенческой группе 15 девушек и 10 юношей. Случайным образом (по жребию) выбирают одного. Найти вероятность того, что отобран будет юноша.

43. При броске игральной кости вычислить вероятности следующих событий:

а) выпало 2 очка;

б) выпало 5 очков;

в) выпало простое число очков;

г) число выпавших очков кратно трем;

д) выпало нечетное число очков.

40. Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 10. Найти вероятность того, что номер первого наудачу извлеченного жетона:

а) не содержит цифру 5;

б) делится без остатка на число 10;

в) делится без остатка на число 7.

40. Найти вероятность того, что наудачу выбранное двузначное число делится:

а) на 8;

б) на 8 и на 3;

в) на 2 , 4 и 6.

40. В урне 6 белых и 4 черных шара. Какова вероятность того, что среди 5 шаров наудачу взятых из урны, будет:

а) 2 белых и 3 черных шаров;

б) 3 белых и 2 черных шаров;

в) 5 белых шаров.

40. В ящике 10 деталей, среди которых две нестандартны. Найти вероятность того, что в наудачу отобранных:

а) двух деталях одна нестандартна;

б) четырех деталях не более двух нестандартных;

в) шести деталях окажется не более одной нестандартной детали.

40. Библиотечка состоит из десяти различных книг. Причем пять книг стоят по 4 рубля каждая, три книги – по одному рублю и две книги – по 3 рубля. Найти вероятность того, что взятые наудачу:

а) две книги стоят 5 рублей;

б) три книги стоят 6 рублей;

в) одна книга стоит 4 рубля.

40. Какова вероятность того, что вынутые из колоды в 36 карт:

а) 2 карты окажутся тузами;

б) 4 карты окажутся тузами;

в) 3 карты окажутся разной масти;

г) 4 карты окажутся разных мастей;

д) 4 карты окажутся одной масти;

е) среди извлеченных 4 карт будет ровно одна дама и ровно один туз.

40. В замке на общей оси пять дисков. Каждый диск разделен на шесть секторов, на которых написаны различные буквы. Замок открывается только в том случае, если каждый диск занимает одно определенное положение относительно корпуса замка. Найти вероятность того, что при произвольной установке дисков замок можно будет открывать.

41. Из 33 букв русского алфавита составляется наугад 5 буквенное слово. Найти вероятность того, что:

а) последняя буква в слове – «а»;

б) последняя буква – гласная;

в) в слове ровно одна бука «а»;

г) в слове ровно одна гласная;

д) в слове ровно две буквы «а»;

е) в слове ровно две гласные.

40. Из 10 арабских цифр составляют наугад 4-хзначное число. Найти вероятность того, что:

1. последняя цифра «2»;

2. число делится на 5;

3. число составлено из разных цифр;

4. число составлено из нечетных цифр;

5. в числе ровно 1 нуль;

6. в числе ровно 3 цифры «3».

54. В мешочке имеется пять одинаковых кубиков. На всех гранях каждого кубика написана одна из следующих букв: О,П,Р,С,Т. Найти вероятность того, что на вынутых по одному и расположенных в одну линию кубиков можно прочесть слово “ спорт”.

55. Из слова “НАУГАД” выбирается одна буква случайным образом. Какова вероятность того, что это буква Я? Какова вероятность того, что это гласная?

56. Из карточек разрезной азбуки сложено слово «ОБОРОНОСПОСОБНОСТЬ». Карточки перемешиваются и раскладываются в ряд случайным образом. Какова вероятность того, что получится слово «НОООБСРПОСТЬСБОООН»

57. В лотерее 100 билетов, из них 40 выигрышных. Какова вероятность того, что когда сначала юноша, а потом девушка вытянут по одному билету, то окажется:

а) что юноша взял выигрышный билет, а девушка – нет;

б) что у девушки оказался выигрышный билет;

в) что у обоих билеты не выигрышные.

54. Студент пришел на экзамен, зная лишь 20 вопросов из 25. Какова вероятность того, что студент вытянет знакомый вопрос, если он тянет билет:

а) первым;

б) вторым;

в) третьим.

54. За круглым столом случайно рассаживаются 6 мужчин и 6 женщин. Какова вероятность того, что мужчины и женщины будут чередоваться друг с другом?

55. Восемь туристов выходят из автобуса и становятся в очередь в кафетерий случайным образом. Найти вероятность того, что два определенных человека А и В окажутся:

а) рядом;

б) отделены друг от друга одним лицом;

в) отделены друг от друга двумя лицами.

54. Внутрь круга радиуса R наудачу брошена точка. Найти вероятность того, что точка окажется:

а) внутри вписанного в круг квадрата;

б) за пределами вписанного в круг квадрата.

54. На плоскости начерчены две концентрические окружности, радиусы которых 5 и 10 см соответственно. Найти вероятность того, что точка, брошенная наудачу в большой круг , попадет:

а) в кольцо, образованное построенными окружностями;

б) в малый круг.

54. Внутрь круга радиуса R брошена точка. Найти вероятность, что точка окажется внутри вписанного в круг:

а) квадрата;

б) правильного треугольника.

54. Плоскость разграфлена параллельными прямыми, отстоящими друг от друга на расстоянии 2а. На плоскость наудачу брошена монета радиуса r < а. Найти вероятность того, что монета не пересеет ни одной прямой.

55. Плоскость разграфлена сетью квадратов прямых, отстоящих друг от друга на расстоянии 2а. На плоскость наудачу брошена монета радиуса r < а. Найти вероятность того, что монета не пересеет ни одной стороны квадрата.

56. На отрезок АВ длины L наудачу брошена точка С с координатой х. Найти вероятность того, что меньший из отрезков АС и ВС имеет длину большую, чем .

57. На отрезок ОА длины L числовой оси ОХ наудачу брошены две точки В(х) и С(у), причем . Найти вероятность того, что длина отрезка ВС меньше длины отрезка ОВ.

58. На отрезок ОА длины L числовой оси ОХ наудачу брошены две точки В(х) и С(у). Найти вероятность того, что длина отрезка ВС меньше расстояния от точки О до ближайшей к ней точки.

59. На отрезок ОА длины L числовой оси ОХ наудачу брошены две точки В(х) и С(у). Найти вероятность того, что длина отрезка ВС окажется меньше, чем .