Проверка статистических гипотез
Статистической называется гипотеза о виде неизвестного распределения или о параметрах неизвестного распределения.
Нулевой
(основной)
гипотезой
называется выдвинутая гипотеза (гипотеза
о равенстве). Конкурирующей
(альтернативной)
гипотезой
называется гипотеза, противоречащая
основной.
Простой называется гипотеза, которая содержит только одно предложение. Сложной называется гипотеза, которая состоит из конечного или бесконечного числа простых гипотез.
Ошибка
первого рода
состоит в том, что отвергается правильная
основная гипотеза. Ошибка
второго рода
состоит в том, что принимается неправильная
основная гипотеза. Вероятность
ошибки первого рода называется уровнем
значимости критерия.
Статистическим критерием называется случайная величина К, которая служит для проверки гипотезы.
Наблюдаемым
(эмпирическим) значением
называется значение критерия, которое
вычислено по выборкам.
Критической
областью
называется совокупность значений
критерия, при которых нулевая гипотеза
отвергается. Левостороннюю критическую
область имеет задача, в которой
конкурирующая гипотеза имеет знак “<”;
правостороннюю – , имеющая знак “>”;
двустороннюю –, имеющая знак “
”.
Областью принятия гипотезы называется совокупность значений критерия, при которых нулевая гипотеза принимается.
Критическими
точками
называются точки, отделяющие критическую
область от области принятия гипотезы.
Критические
точки определяются при заданном уровне
значимости
следующими выражениями:
- для правосторонней критической области:
,
- для левосторонней критической области:
,
- для двухсторонней критической области:
.
Мощность критерия - это вероятность попадания критерия в критическую область при условии, что справедлива конкурирующая гипотеза.
Сравнение двух дисперсий нормальных генеральных совокупностей (Критерий Фишера)
Исходные
данные: Две независимые выборки, объемы
которых
и
,
извлечены из нормальных генеральных
совокупностей и найдены исправленные
дисперсии
и
.
Нулевая гипотеза : D(X) = D(Y).
Конкурирующая
гипотеза
: D(X)>D(Y).
Для проверки нулевой гипотезы вычисляется наблюдаемое значение критерия
,
если
.
В противном случае
.
Нулевая
гипотеза принимается, если
,
где
- критическая точка, определяемая по
таблице распределения Фишера-Снедекора
при заданном уровне значимости
и числом степеней свободы
,
где
– объем выборки, имеющей большую
исправленную дисперсию (иначе поменять
X и Y местами).
Если
,
то нулевая гипотеза отвергается.
При
конкурирующей гипотезе
:
.
Сравнение двух средних генеральных совокупностей
Исходные
данные: Две независимые выборки объема
и
больших объемов (
>30,
>30),
по которым найдены выборочные средние
и
.
Генеральные дисперсии D(X) и D(Y) - известны.
Нулевая гипотеза : M(X)=M(Y).
Конкурирующая
гипотеза
:
.
Наблюдаемое значение критерия
Нулевая
гипотеза принимается, если
,
где критическая точка
находится по таблице Лапласа из условия,
что
.
Если
- нулевая гипотеза отвергается.
При
конкурирующей гипотезе
критическая точка находится из условия:
.
Если
,
то нулевая гипотеза отвергается.
Если генеральные дисперсии D(X) и D(Y) неизвестны и одинаковы, а и – объемы малых независимых выборок, то наблюдаемое значение критерия
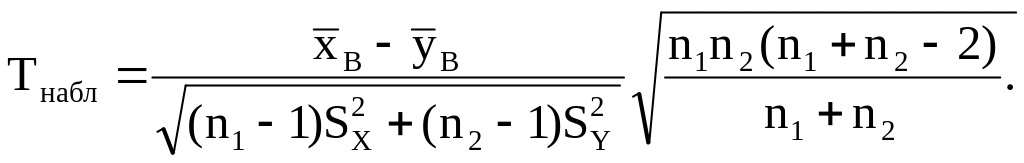
Нулевая гипотеза принимается, если
,
где
критическая точка
находится по таблице распределения
Стьюдента при заданном уровне значимости
и числу степеней свободы
.
Нулевая
гипотеза отвергается, если
.
В случае такого условия, если достоверно неизвестно, что дисперсии генеральных совокупностей одинаковы, приходится предварительно использовать критерий Фишера для проверки гипотезы о равенстве дисперсий нормальных генеральных совокупностей по найденным исправленным дисперсиям.