Уравнение линейной регрессии. Выборочный коэффициент корреляции

Статистической называется зависимость, при которой изменение одной из величин влечет за собой изменение распределения другой.

Корреляционной зависимость Y от Х называется функциональная зависимость условной средней от Х, т.е.

=f(x), (1)

где условное среднее - это среднее арифметическое значение Y, соответствующее значению Х=х. Приведенное уравнение (1) называется уравнением регрессии, а функция f(x), называется регрессией Y на Х, а ее график – линией регрессии Y на Х.

Теория корреляции решает две задачи:

– установление формы корреляционной связи, т.е. вида функции регрессии;

– оценка тесноты корреляционной связи.

Отыскание параметров выборочного уравнения прямой линии регрессии

Для отыскания параметров выборочного уравнения прямой линией регрессии используются данные независимых экспериментов . Причем функция регрессии f(x) задается линейной относительно параметров регрессии, т.е. в случае парной регрессии

Для нахождения параметров используется метод наименьших квадратов. В случае линейной зависимости, т.е.

,

в соответствии с методом наименьших квадратов параметры a и b подбираются таким образом, чтобы функционал

Так как минимизация данного функционала требует дифференцирования его по каждой переменной, то это приводит к следующей системе уравнений:

;

.

После преобразования получается система двух линейных уравнений, в результате решения которых находятся параметры регрессии a и b.

Замечание 1. Рассмотренный способ нахождения оценок параметров а и b (метод наименьших квадратов) можно распространить на другие зависимости f(x): и другие.

Оценка тесноты корреляционной зависимости

Оценкой тесноты корреляционной зависимости является выборочный коэффициент корреляции.

,

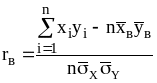где за обозначены выборочные среднеквадратические отклонения по X и по Y.

Свойства выборочного коэффициента корреляции

1. Абсолютная величина коэффициента не превосходит 1, то есть .

2. Если =0, то Y и Х не связаны линейной корреляционной зависимостью.

3. Если =1, то Y и Х связаны линейной корреляционной зависимостью.

4. С возрастанием абсолютного значения линейная корреляционная зависимость становится более тесной и при =1 переходит в функциональную зависимость.

Замечание 2. Коэффициент корреляции связан с коэффициентом линейной регрессии b зависимостью вида:

.

Зная точечные оценки составляющих Х и Y, можно записать уравнение линейной регрессии Y на Х в виде:

.

Интервальная оценка выборочного коэффициента корреляции

Интервальной оценкой выборочного коэффициента корреляции с надежностью называется доверительный интервал:

где n – объем выборки, а t – коэффициент, находимый по таблице функции Лапласа (см. прил., табл. 3) из соотношения . Формула используется при значительных объемах выборки.

Нахождение коэффициента корреляции по корреляционной таблице

Пусть эмпирические данные представлены в виде корреляционной таблицы:

X Y

В таблице – значения признака X; – значения признака Y; – частота появления в выборке пары .

Тогда выборочный коэффициент корреляции может быть найден по формуле:

,

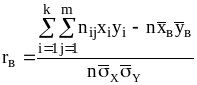где n – сумма всех частот корреляционной таблицы (объем выборки).

Задачи

38. Зависимость месячной прибыли фирмы Y (тыс. усл. ед.) представлена в таблице

x	0,1	0,11	0,12	0,13	0,14	0,15
y	7,16	6,78	6,39	6,24	6,30	6,11

Нарисовать корреляционное поле, по его виду выбрать функцию регрессии Y и Х и найти ее параметры.

39. Зависимость урожая Y(ц/га) сельскохозяйственной культуры от уровня дождей Х (в условных единицах) в летний период представлена в таблице

x	10	15	20	25	30	35	40
y	10,668	14,775	16,587	18,295	18,126	14,479	8,242

Нарисовать корреляционное поле, по его виду выбрать функцию регрессии Y и Х и найти ее параметры.

40. В таблице приведены данные о зависимости стоимости эксплуатации самолета Y (млн. руб.) от его возраста Х (лет).

x	1	2	3	4	5	6	7	8
y	3	3,5	3,5	4	4	6	9	10

Нарисовать корреляционное поле, по его виду выбрать функцию регрессии Y и Х и найти ее параметры.

41. В таблице указаны курс акций – и эффективность рынка –

	10	9	9	10	10	11	12	10	9	10
	15	13	14	15	16	17	16	15	14	15

Найти зависимость курса акций от эффективности рынка.

43. В таблице приведены данные об индексе розничных цен на пищевые товары (X) и индексе промышленного производства (Y). Записать уравнение регрессии, по которому можно прогнозировать индекс производства.

Индекс цен	100	101	113	115	113	113	111	112	115	129
Индекс производства	64	75	81	91	91	85	96	99	100	93

44. Имеются следующие данные по десяти шахтам о сменной добыче угля на одного рабочего (т) и мощности пласта (м):

	8	11	12	9	8	8	9	9	8	12
	5	10	10	7	5	6	6	5	6	8

Построить уравнение регрессии: зависимости добычи угля от мощности пласта.

46. В таблице приведены данные о связи между ценой на нефть Х (ден. ед.) и индексом нефтяных компаний Y (усл. ед.). Предполагая, что связь между величинами Х и Y линейна, найти функцию регрессии.

X	11,0	11,5	12,0	12,5	13,0	13,5
Y	1,5	1,5	1,6	1,7	1,9	1,9

48. Для данных таблицы найти коэффициенты линейного уравнения регрессии.

Х y	0,4	0,8	1,0	1,2	1,8	2,0
3,0	2	3	-	-	-	-
3,5	-	4	2	1	-	-
4,5	-	-	1	2	2	-
5,0	-	-	-	-	2	1

50. Найти линейное уравнение регрессии по данным таблицы

Х y	0,4	0,8	1,0	2,0
2-6	-	-	1	2
6-10	-	1	3	1
10-14	1	2	1	-
14-18	2	1	1	-
18-22	1	3	-	-