Методы нахождения точечных оценок неизвестных параметров распределения Не надо метод максимального правдоподобия

Пусть дана выборка объема n из генеральной совокупности Х и задан закон распределения с точностью до неизвестного параметра . Для того, чтобы получить точечную оценку неизвестного параметра с помощью метода максимального правдоподобия необходимо:

1. Построить функцию правдоподобия

;

2. Найти логарифмическую функцию правдоподобия ;

3. Найти точку максимума , для чего решить уравнение:

.

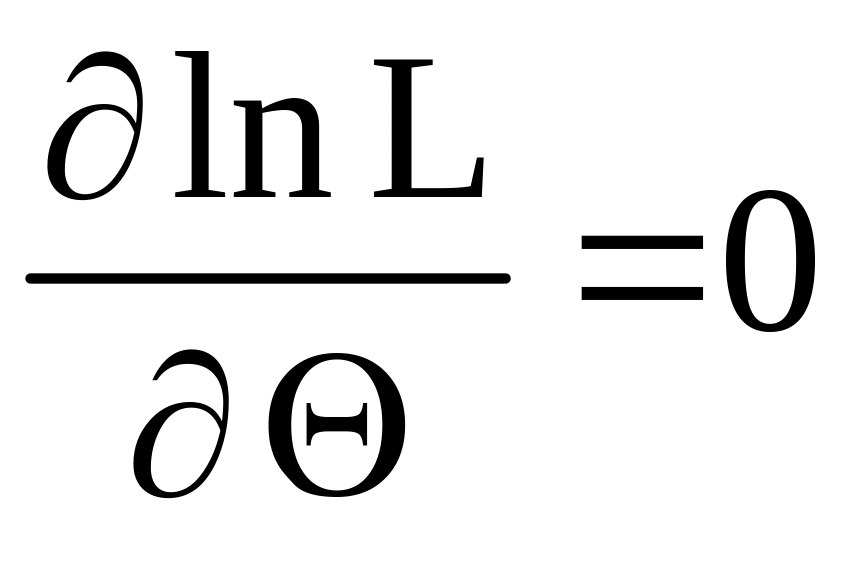Точка , доставляющая максимум функции , является оценкой максимального правдоподобия неизвестного параметра .

Замечание. Все переменные функции правдоподобия, кроме , считаются фиксированными.

Надо задачи

10. Случайная величина Х (число поврежденных стеклянных изделий в одном контейнере) распределена по закону Пуассона с неизвестным параметром :

Ниже приведено эмпирическое распределение числа поврежденных изделий в 500 контейнерах. Впервой строке указано количество поврежденных изделий в одном контейнере, во второй строке приведена частота – число контейнеров, содержащих поврежденных изделий.

	0	1	2	3	4	5	6	7
	199	169	87	31	9	3	1	1

Интервальные оценки неизвестных параметров распределения

Интервальной называется оценка неизвестного параметра теоретического распределения, определяемая двумя числами – концами интервала. Если - параметр теоретического распределения, - его точечная статистическая оценка, то точность интервальной оценки определяется из равенства

,

где - малое положительное число.

Надежностью (доверительной вероятностью) называется вероятность, с которой осуществляется неравенство , т.е.

.

Доверительным интервалом называется интервал покрывающий неизвестный параметр с заданной надежностью .

Интервальные оценки математического ожидания нормального распределения

Интервальной оценкой математического ожидания нормального распределения:

• при известном среднеквадратическом отклонении является доверительный интервал

.

• при неизвестном среднеквадратическом отклонении является доверительный интервал

,

с надежностью ,

где - выборочное среднее; S - исправленное среднеквадратическое отклонение; n – объем выборки; t – аргумент функции Лапласа, определяемого по таблице 3 функции Лапласа (см. приложение, таблицу 3) из соотношения ; - величина, определяемая по таблице 4 распределения Стьюдента (см. приложение, таблицу 4) при заданных n и  .

Интервальные оценки среднеквадратического отклонения

нормального распределения

Интервальной оценкой среднеквадратического отклонения нормального распределения с надежностью по исправленному среднеквадратическому отклонению S называется доверительный интервал

(при q <1),

где и находится по таблице 7 значений q при заданных n и (см. приложение, таблицу 7).

Интервальная оценка неизвестной вероятности

биномиального распределения

Интервальной оценкой неизвестной вероятности p биномиального распределения по относительной частоте w с надежностью называется доверительный интервал вида , где

,

,

где n – объем выборки; t- значение аргумента функции Лапласа, причем (см. приложение, таблицу 3).

При больших значениях n в качестве приближенных границ доверительного интервала принимаются:

,

.

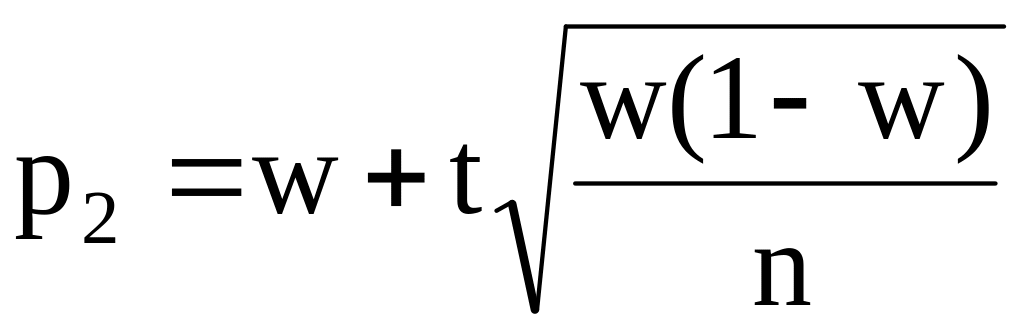1. Одним и тем же прибором со среднеквадратическим отклонением случайных ошибок измерений =40м произведено 5 равноточных измерений расстояний от орудия до цели. Найти доверительный интервал для оценки истинного расстояния до цели с надежностью =0,95, зная среднее арифметическое результатов измерений = 2000м. Предполагается, что результаты измерений распределены нормально.

2. По данным 16 независимых равноточных измерений некоторой физической величины найдены среднее арифметическое результатов измерений =42,8 и исправленное среднеквадратическое отклонение S=8. Оценить истинное значение измеряемой величины с надежностью =0,999.

3. Произведено 10 измерений одним прибором (без систематической ошибки) некоторой физической величины, причем исправленное среднеквадратическое отклонение S случайных ошибок измерений оказалось равным 0,8. Найти точность прибора с надежностью 0,95. Предполагается, что результаты измерений распределены нормально.

4. При формировании для фирмы портфеля поставок был произведен случайный повторный отбор 100 поставщиков, которые осуществляли поставки сырья в прошлом году. Для процента несвоевременно отгрузивших сырье поставщиков необходимо определить доверительные границы на уровне 0,997, если в выборке оказалось 25 таких поставщиков.

5. В выборке объемом 500 единиц, произведенной для определения процента всхожести зерна, установлена частость доброкачественных зерен 0,94. Найти вероятность процента всхожести, если допустимая погрешность в его определении равна 2 %.

6. Определить численность выборки при обследовании остатков на расчетных счетах у клиентов банка, чтобы с вероятностью 0,683 предельная ошибка равнялась 5 усл. ед., если = 120 усл. ед.

7. В табл. 10 приведены результаты выборочного обследования заработной платы Х ста рабочих предприятия, на котором занято 1000 рабочих.

Таблица 10

Заработная плата,тыс. руб.	100-120	120-140	140-160	160-180	180-200
Число рабочих	17	40	32	8	3

8. Найти интервальные оценки математического ожидания и дисперсии. Считая случайную величину Х распределенной по закону, близкому к нормальному.

9. По данным 10 измерений некоторой величины Х найдено среднее = 20 и выборочная дисперсия 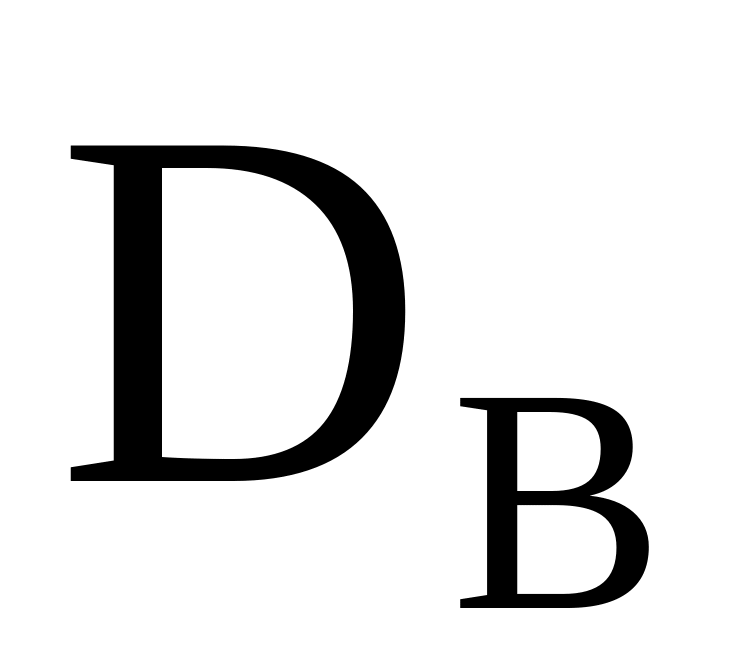 = 25. Найти границы, в которых с вероятностью 0,99 заключено истинное значение величины.

10. Для оценки уровня безработицы в городе были отобраны 100 человек рабочих специальностей. Из них 6 человек оказались безработными. Оценить с вероятностью 0,95 процент Р безработных рабочих в городе.

11. При выборочном обследовании 100 телезрителе оказалось, что 35 из них регулярно смотрят программы НТВ. Построить 99%-ный доверительный интервал для доли Р всех телезрителей, предпочитающих канал НТВ.

12. Для оценки стоимости древесины, с целью последующей продажи, была сделана выборка из 100 деревьев участка, подлежащих вырубке. В результате измерения диаметров Х деревьев были получены среднее значение 50 см и выборочная дисперсия = 3,5. Определить на уровне 0,95 доверительный интервал для диаметра Х деревьев, подлежащих вырубке.

13. Для определения привеса рыбы за год в одном из рыбхозов Любанского района проводились выборочные исследования. Разводимые в пруду карпы вылавливались, взвешивались и отпускались обратно. Результаты 100 таких измерений показали, что годовой привес рыбы в среднем составил 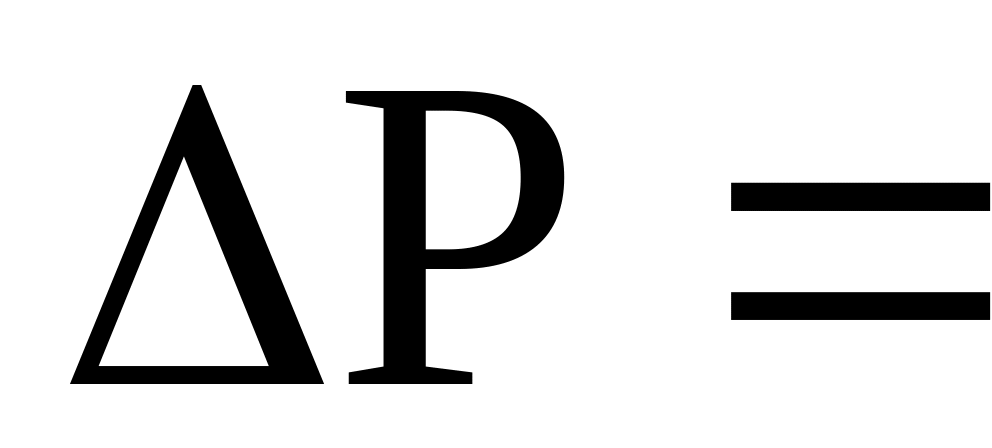200г, а дисперсия – =320 . Найти 95%-ный доверительный интервал для годового привеса рыбы.

14. Из 10 орехов, взятых для проверки, 2 оказались «пустыми». Найти 95%-ный доверительный интервал для доли «пустых» орехов в продаваемой партии.

15. На овцеводческой ферме из стада произведена выборка для взвешивания 36 овец. Их средний вес оказался равным 50 кг. Предположив распределение веса нормальным и определив несмещенную оценку выборочной дисперсии 16, найти доверительный интервал для оценки математического ожидания с надежностью а) 0,8; б) 0,9; в) 0,95.

16. В нескольких мелких магазинах проведена проверка качества 100 изделий, после чего осуществлена обработка полученных данных. В результате получено несмещенное значение выборочного среднего квадратичного отклонения S = 4. Считая распределение качественных изделий нормальным, найти с надежностью 0,95 доверительный интервал для оценки среднего квадратичного отклонения.

17. По результатам социологического обследования при опросе 1500 респондентов рейтинг президента (т.е. процент опрошенных, одобряющих его деятельность) составил 30 %. Найти границы, в которых с надежностью 0,95 заключен рейтинг президента (при опросе всех жителей страны). Сколько респондентов надо опросить, чтобы с надежностью 0,99 гарантировать предельную ошибку социологического обследования не более 1 %? Тот же вопрос, если никаких данных о рейтинге президента нет.

18. Из 5000 вкладчиков банка по схеме случайной бесповторной выборки было отобрано 300 вкладчиков. Средний размер вклада в выборке составил 8000 руб., а среднеквадратическое отклонение 2500 руб. Какова вероятность того, что средний размер вклада случайно выбранного вкладчика отличается от его среднего размера в выборке не более, чем на 100 руб. (по абсолютной величине)?

19. Выборка из большой партии электроламп содержит 100 ламп. Средняя продолжительность горения лампы выборки оказалась равной 1000 часов. Найти с надежностью 0,95 доверительный интервал для средней продолжительности горения лампы всей партии, если известно, что среднеквадратическое отклонение продолжительности горения лампы  часов. Предполагается, что результаты измерений распределены нормально.

20. Станок автомат штампует валики. По выборке объема n=100 найдено выборочное среднее диаметров изготовленных валиков. Найти с надежностью 0,95 точность , с которой выборочное среднее оценивает математическое ожидание диаметров изготовляемых валиков, зная, что их среднее квадратическое отклонение =2мм. Предполагается, что диаметры валиков распределены нормально.

21. Из генеральной совокупности извлечена выборка объема n=12.

	-0,5	-0,4	-0,2	0	0,2	0,6	0,8	1	1,2	1,5
	1	2	1	1	1	1	1	1	2	1

Оценить с надежностью 0,95 математическое ожидание нормально распределенного признака генеральной совокупности с помощью доверительного интервала.

22. Каким должен быть объем выборки, отобранной по схеме случайной бесповторной выборки из партии, содержащей 8000 деталей, чтобы с вероятностью 0,994 можно было утверждать, что доли первосортных деталей в выборке и во всей партии отличаются не более чем на 0,05 (по абсолютной величине)? Задачу решить для случаев: а) о доле первосортных деталей во всей партии ничего не известно; б) их не более 80 %.

23. Найти минимальный объем выборки, при котором с надежностью 0,925 точность оценки математического ожидания нормально распределенной генеральной совокупности по выборочному среднему равна 0,2 , если известно среднеквадратическое отклонение =1,5.

24. Найти минимальный объем выборки, при котором с надежностью 0,99 точность оценки математического ожидания генеральной совокупности по выборочному среднему равна =0,2, если известно среднеквадратическое отклонение =1,2 , нормально распределенной генеральной совокупности.