Точечные оценки параметров распределения
Точечной
называется статистическая оценка,
которая определяется одним числом
,
где
- результаты n наблюдений над количественным
признаком Х.
Статистическая
оценка
называется
несмещенной,
если
где
– оцениваемый параметр теоретического
распределения.
Если
,
статистическая оценка называется
смещенной.
Статистическая оценка называется состоятельной, если
,
где
- сколь угодно малое положительное
число.
Статистическая оценка называется эффективной, если данная оценка имеет наименьшую возможную дисперсию среди оценок данного параметра, сделанным по выборкам одинакового объема.
Выборочная средняя
или
где n – объем выборки, а k –количество различных вариант в выборке.
Выборочная и исправленная дисперсии
Выборочная дисперсия
,
или
.
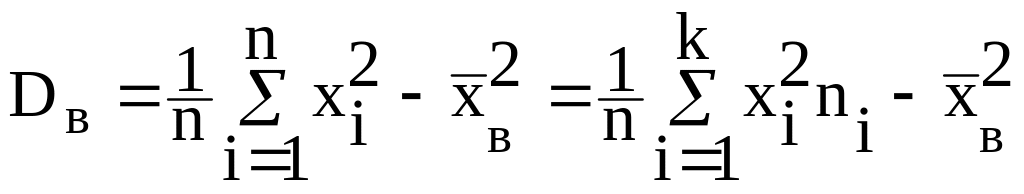В отличие от выборочной дисперсии DВ являющейся смещенной оценкой генеральной дисперсии, исправленная дисперсия является несмещенной оценкой и определяется по выражению
,
или
.
Выборочное и исправленное среднеквадратическое отклонение
.
Мода и медиана выборки
Модой
называется варианта, имеющая наибольшую
частоту или относительную частоту.
Для непрерывной выборки, заданной в виде интервального ряда, мода находится по формуле:
,
где
– начало модального интервала; h
– его длина;
–
его частота;
– частота интервала, предшествующего
модальному;
– частота интервала, следующего за
модальным.
Медианой выборки Ме называется варианта, которая делит вариационный ряд на две части, равные по числу вариант. Для дискретной выборки, при нечетном числе вариант n
,
а при четном числе вариант n
.
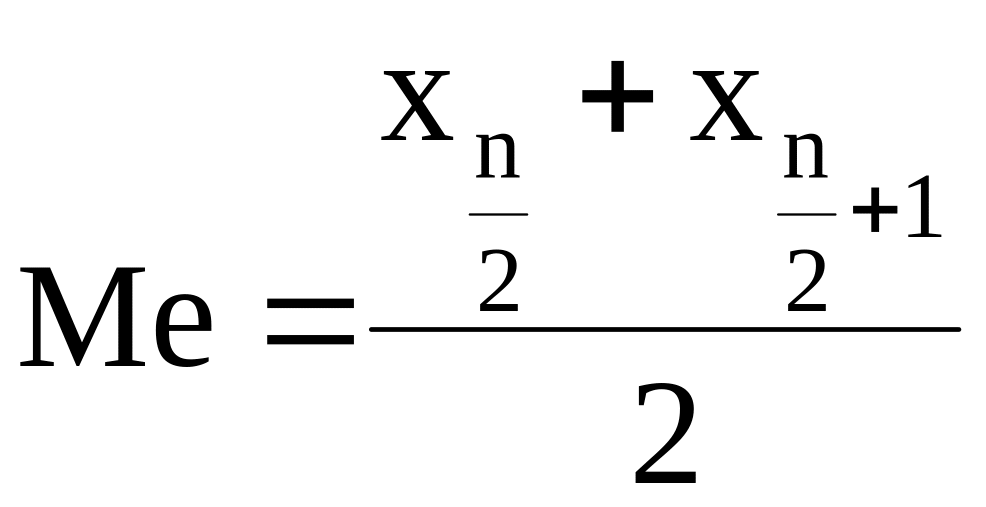Для непрерывной выборки, заданной в виде интервального ряда, медиана находится по формуле:
,
где n
– объем выборки;
– начало медианного интервала; h
– его длина;
–
его частота;
– накопленная частота интервала,
предшествующего медианному.
Не надо Асимметрия и эксцесс выборки
Асимметрия эмпирического распределения
,
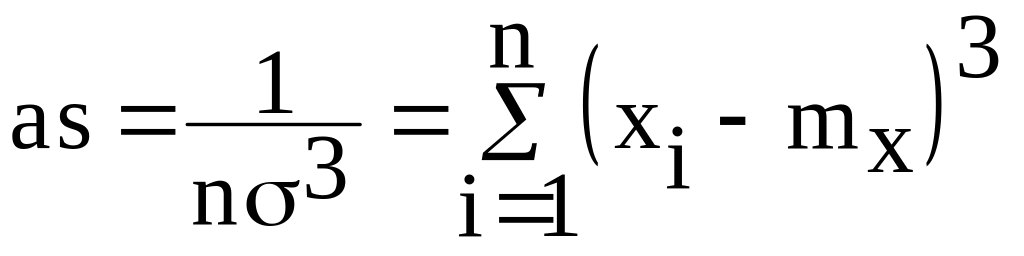или
.
Эксцесс эмпирического распределения
,
или
.
Пример 2.
Найти выборочное среднее и выборочную дисперсию по распределению выборки объема n=10:
|
26,1 |
26,3 |
26,7 |
27,4 |
|
2 |
3 |
4 |
1 |
Решение.
Если варианты являются дробными числами (особенно дробями много меньшими единицы), то целесообразно перейти при расчете к условным вариантам, умножив каждое на коэффициент масштабирования k. Если взять k=10, то получим числа без десятичной запятой: 261, 263, 267, 274.
Если полученные условные варианты являются большими числами, имеет смысл прибавить к каждому из них условный ноль С, с целью преобразовать их в варианты небольшие по абсолютному значению. В данном случае удобно положить С= - 267.
Таким образом,
преобразование
к
условным вариантам
в данном случае заключается в следующем:
.
Распределение условных вариант имеет вид:
|
- 6 |
- 4 |
0 |
7 |
|
2 |
3 |
4 |
1 |
Для нахождения выборочного среднего и выборочной дисперсии с помощью условных вариант используем формулы п.4.1 и п. 4.2., заменив в них на .
Нетрудно показать,
что для того, чтобы выразить из полученного
результата
,
достаточно воспользоваться формулой:
.
Откуда
.
Найдем далее дисперсию в условных вариантах:
Искомую выборочную дисперсию (для первоначальных вариант) найдем по формуле:
.
ЗАДАЧИ
8. Ниже приведены результаты измерения роста (в см) случайно отобранных 100 студентов.
рост |
154-158 |
158-162 |
162-166 |
166-170 |
170-174 |
174-178 |
178-182 |
число студ. |
10 |
14 |
26 |
28 |
12 |
8 |
2 |
Найти выборочную среднюю, выборочную дисперсию, исправленную дисперсию, выборочное среднеквадратическое отклонение роста обследованных студентов.
9. Вычислить коэффициенты асимметрии и эксцесса для выборки, характеризующей горизонтальное отклонение от цели (м) для 200 испытаний ракет.
гр. инт. |
-40 – -30 |
-30 – -20 |
-20 – -10 |
-10 – 0 |
0–10 |
10–20 |
20–30 |
30–40 |
40–50 |
50–60 |
част |
7 |
11 |
15 |
24 |
49 |
41 |
26 |
14 |
7 |
3 |
10. Вычислить коэффициенты асимметрии и эксцесса для выборки, характеризующей пределы прочности образцов варки (н/мм):
гран. интерв. |
28-30 |
30-32 |
32-34 |
34-36 |
36-38 |
38-40 |
40-42 |
42-44 |
частоты |
8 |
15 |
15 |
12 |
15 |
20 |
10 |
5 |
11. Вычислить коэффициенты асимметрии и эксцесса для выборки, характеризующей число набранных баллов в соревнованиях:
гран. интерв. |
49-52 |
52-55 |
55-58 |
58-61 |
61-64 |
64-67 |
67-70 |
частоты |
3 |
6 |
11 |
19 |
30 |
21 |
10 |
12. Определить выборочные среднюю и дисперсию: а) по несгруппированной выборке объема n=44;
-
17
21
8
20
23
18
22
20
20
17
12
20
11
9
19
20
9
19
19
17
21
13
17
22
22
10
20
20
15
15
19
20
20
13
21
21
9
14
11
19
19
18
23
19
б) по сгруппированной выборке с длиной интервала h=2.
Сравнить результаты вычислений.
13. Определить выборочные среднюю и дисперсию: а) по не сгруппированной выборке объема n=36;
-
8,5
7,1
6,7
6,2
2,9
4,4
6,0
5,8
5,4
8,2
6,9
6,5
6,1
3,8
6,0
6,0
5,6
5,3
7,7
6,8
6,5
6,1
4,2
4,7
5,6
5,4
5,3
7,4
6,7
6,4
6,1
4,5
6,0
5,8
5,6
5,1
б) по сгруппированной выборке с длиной интервала h=1.
Сравнить результаты вычислений.
14. Контрольные обмеры диаметров болтов дали следующие результаты: 2,31; 2,28; 2,29; 2,28; 2,32; 2,28; 2,32; 2,29; 2,31; 2,32. Найти выборочную среднюю, дисперсию и среднеквадратическое отклонение, перейдя к условным вариантам.
15. Вычислить моду, медиану, выборочную среднюю, дисперсию и среднеквадратическое отклонение, исправленную дисперсию выборки: 3,1; 3,0; 1,5; 1,8; 2,5; 3,1; 2,4; 2,8; 1,3, перейдя к условным вариантам.
16. Измерительным прибором, практически не имеющим систематической погрешности, сделано пять независимых измерений некоторой величины
-
Номер измерения
1
2
3
4
5
Значение
величины
2781
2836
2807
2763
2858
а) найти выборочную дисперсию погрешности измерения, если измеряемая величина точно известна: 2800;
б) найти выборочную среднюю, дисперсию и ее несмещенную оценку, если точное значение измеряемой величины неизвестно, перейдя к условным вариантам.
17. На телефонной станции производились наблюдения за числом неправильных соединений в минуту. Наблюдения в течение часа дали следующие результаты:
-
3
1
3
4
2
1
1
3
2
7
2
0
2
4
0
3
0
2
0
1
3
3
1
2
2
0
2
1
4
3
4
2
0
2
3
1
3
1
4
2
2
1
2
5
1
1
0
1
1
2
1
0
3
4
1
2
2
1
1
5
Найти выборочную среднюю, дисперсию и ее несмещенную оценку.