Первичная обработка выборки. Точечные оценки неизвестных параметров распределения

Генеральная совокупность это множество всех объектов, которые должны быть исследованы. Пусть для изучения количественного признака Х генеральной совокупности извлечена выборка объема n. Ранжированный ряд получается, если упорядочить выборку по возрастанию. Различные наблюдавшиеся значения признака Х называются вариантами, а числа , показывающие сколько раз каждая варианта встретилась в выборке – соответствующими им частотами (или относительными частотами  ). Последовательность вариант, записанная в порядке возрастания, с указанием их частот ( ), называется вариационным рядом.

Вариационный ряд называется дискретным, если выборка сделана из множества значений дискретной случайной величины Х, непрерывным, если выборка сделана из множества значений непрерывной случайной величины.

Общий вид дискретного вариационного ряда:

хi	x1	x2	…	xk
ni	n1	n2	…	nk

Здесь х_i – варианты, n_i – соответствующие им частоты.

Общий вид интервального вариационного ряда:

[аi;аi+1)	[a1;a2)	[a2;a3)	…	[ak;ak+1)
ni	n1	n2	…	nk

Здесь а_i – границы частичных интервалов. На которые разбивается выборка, n_i – соответствующие им частоты (количество выборочных данных, попавших в i-ый интервал.).

Эмпирическая функция распределения

Эмпирической функцией распределения называется функция, определяющая для каждого значения х относительную частоту события X<x, тo есть

,

где - число вариант, меньших

Свойства функции .

1. .

2. – неубывающая функция, т.е. , если .

3. Если – наименьшая варианта, то , при .

4. Если – наибольшая варианта, то , при .

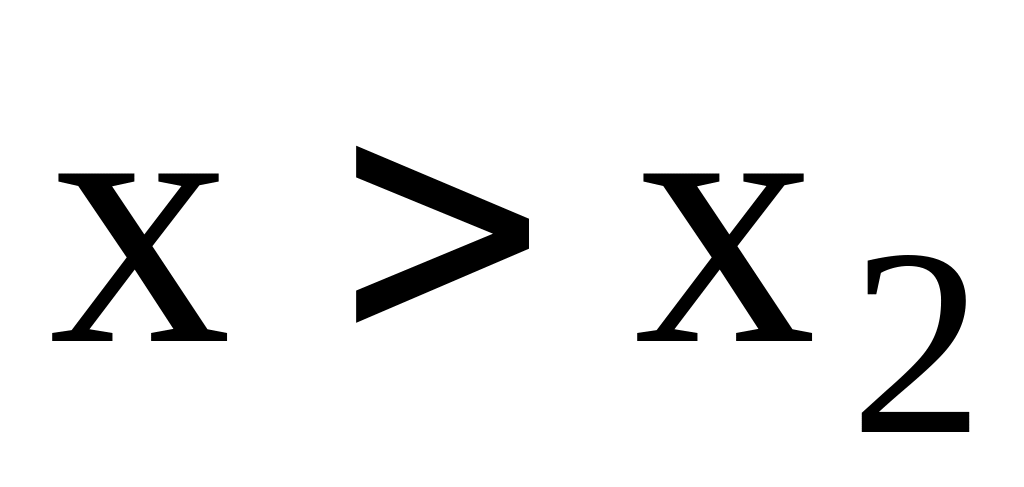Полигон и гистограмма

Полигоном частот называют, ломаную кривую, отрезки которой соединяют точки . Пример полигона частот приведен на рис.1.

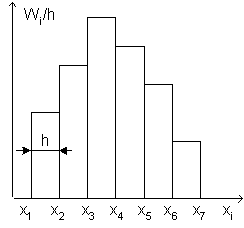
Рис. 1. Полигон частот Рис. 2. Гистограмма

относительных частот

Полигоном относительных частот называют ломанную кривую, отрезки которой соединяют точки .

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению (плотности частоты). Площадь гистограммы частот равна объему выборки n.

Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению (плотности относительной частоты). Площадь гистограммы относительных частот равна единице. Пример гистограммы относительных частот приведен на рис.2.

Пример. Найти эмпирическую функцию распределения по распределению выборки.

	15	20	25	30	35
	10	15	30	20	25

Решение.

Воспользуемся формулой:

,

где n – объем выборки (n=10+15+30+20+25=100),

– число вариант, меньших аргумента x. Так как является кусочно-постоянной (ступенчатой), разобьем область определения R на интервалы постоянства функции (см рисунок).

0 15 20 25 30 35

1. При x 15

вариант, меньших x в выборке нет, то есть = 0.

.

2. При 15<x 20

варианты, меньшие x – это 10 вариант, каждая из которых равна 15, то есть =10. .

3. При 20<x 25

вариант, меньших x – двадцать пять:

10 – равных 15 и 15 – равных 20, то есть =10+15=25. .

4. При 25<x 30

вариант, меньших x – пятьдесят пять:

10 – равных 15, 15 – равных 20, 30 – равных 25, то есть =10+15+25=55.

.

5. При 30<x 35

вариант, меньших x – семьдесят пять:

10 – равных 15, 15 – равных 20, 30 – равных 25, 20 – равных 30, то есть =10+15+25+30=75. .

6. При x>35

все 100 вариант меньше х. .

Таким образом, эмпирическая функция распределения имеет вид:

.

ЗАДАЧИ

1. Найти эмпирическую функцию распределения по распределению выборки:

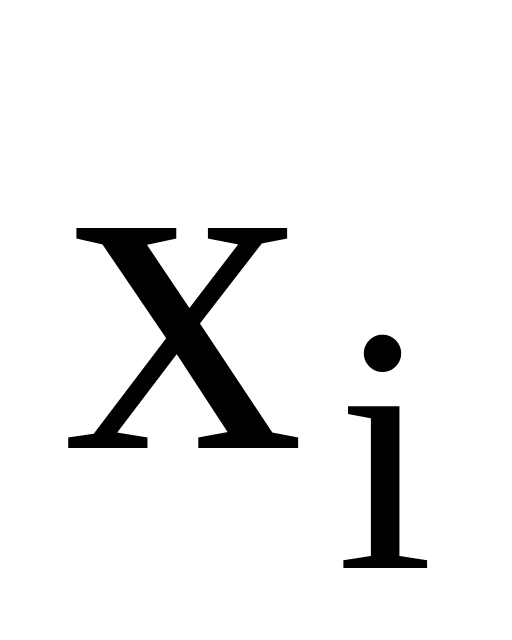
	1	4	6
	10	15	25

и построить ее график.

2. Построить полигон относительных частот по распределению выборки:

	15	20	25	30	35
	10	15	30	20	25

3 Построить гистограмму частот и полигон относительных частот по

распределению выборки:

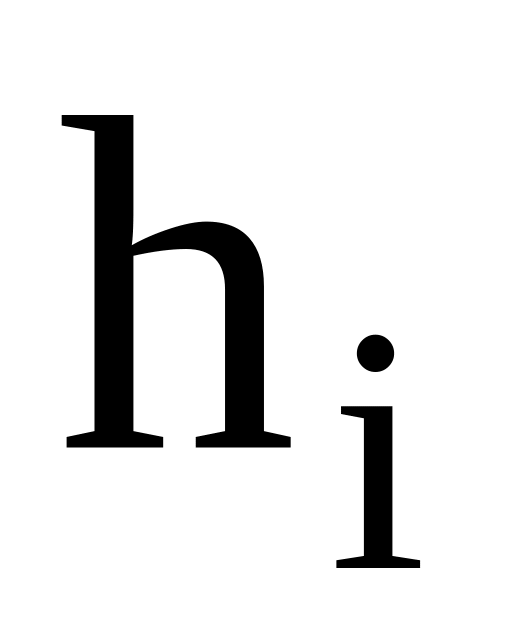
	10 - 15	15 - 20	20 - 25	25 - 30	30 - 35
	2	4	6	4	2

4.Время решения контрольной задачи учениками четвертого класса в секундах приведено в табл.3.

Таблица 3.

38	60	41	51	33	42	45	21	53	60
68	52	47	46	49	49	14	57	54	59
77	47	28	48	58	32	42	58	61	30
61	35	47	72	41	45	44	55	30	40
67	65	39	48	43	10	42	59	50	54

Сгруппировать выборку с длиной интервала h=10 секунд и построить вариационный ряд и полигон частот, эмпирическую функцию распределения.

5. Продолжительность времени работы электронных ламп одного типа в часах приведена в таблице 4.

Таблица 4.

13,4	14,7	15,2	15,1	10,0	13,0	10,8	14,0	17,9	15,1
16,5	16,6	14,2	19,8	16,3	14,6	11,7	16,4	15,1	17,6
14,1	18,8	11,6	13,9	18,0	12,4	17,2	14,5	16,3	13,4
15,5	16,2	18,4	14,7	15,4	11,3	10,7	16,9	15,8	15,3
16,1	12,3	14,0	17,7	14,7	16,2	17,1	18,3	10,1	15,8
18,3	19,8	17,5	12,7	19,7	13,5	14,0	14,0	14,0	15,7
11,9	14,3	12,1	12,1	10,9	17,7	17,7	15,4	15,4	10,9
18,2	18,2	17,3	17,3	15,2	15,2	16,7	17,3	12,1	19,2

Сгруппировать выборку с длиной интервала h=0,9 часа и построить полигон частот, эмпирическую функцию распределения.

6. В опытах наблюдалась неотрицательная случайная величина Х. Ее упорядочение по величине значения и округление с точностью до 0,01 при n=50 опытов приведены в табл. 5.

Таблица 5.

0,00	0,01	0,04	0,17	0,18	0,22	0,22	0,25	0,25	0,29
0,42	0,46	0,47	0,47	0,56	0,59	0,67	0,68	0,70	0,72
0,76	0,78	0,83	0,85	0,87	0,93	1,00	1,01	1,01	1,02
1,02	1,02	1,32	1,34	1,37	1,47	1,50	1,53	1,54	1,59
1,71	1,90	2,10	2,35	2,46	2,46	2,50	2,73	3,07	3,93

Сгруппировать выборку с длиной интервала 0,8 и построить гистограмму частот. Найти моду и медиану полученного интервального ряда.

7. Время реакции водителя на опасность возникновения ДТП в секундах приведено в табл.6.

Таблица 6.

8,5	7,1	6,7	6,2	2,9	4,4	6,0	5,8	5,4
8,2	6,9	6,5	6,1	3,8	6,0	6,0	5,6	5,3
7,7	6,8	6,5	6,1	4,2	4,7	5,6	5,4	5,3
7,4	6,7	6,4	6,1	4,5	6,0	5,8	5,6	5,1

Построить вариационный ряд, сгруппировать выборку с длиной интервала h=0,7 сек. и построить гистограмму частот.