1.3. Расчет упругих стержневых конструкций при ударном нагружении.

Явление удара наблюдается, когда скорости соприкасающихся тел изменяются в течение очень малого промежутка времени. Напряжения и деформации при ударном нагружении, называемые динамическими, оказываются значительно большими, чем те, которые возникли бы в данной системе при статическом приложении той же нагрузки. Процесс удара жесткого груза об упругую стержневую систему протекает следующим образом. Сначала груз, движущийся с некоторой скоростью, входит в соприкосновение с системой, скорость его движения резко уменьшается. Упругая система приходит в движение. Однако вследствие инерции массы системы ее частицы начинают перемещаться не одновременно. Чтобы волна деформации распространилась от места удара по всей системе, требуется время. В стальных конструкциях волна деформации сжатия-растяжения распространяется со скоростью более 5000 м/с. После соприкосновения груз движется совместно с воспринимающей удар упругой системой, причем скорость их движения постепенно уменьшается и становится равной нулю при наибольшей деформации. Затем начинается обратное движение, в дальнейшем система совершает колебательные движения.

Ввиду недостаточной изученности расчет на прочность при динамической нагрузке обычно ведут по статическим прочностным характеристикам материала, условие прочности имеет вид: , где - максимальное расчетное напряжение при ударе.

При ударе возникают деформации двух типов: местные деформации в зоне контакта и общие деформации системы. В дальнейшем рассматриваются только общие деформации системы, и предполагается, что динамические напряжения не превосходят предел пропорциональности материала.

Для приближенного определения напряжений и перемещений сечений в момент наибольшей деформации системы в практических расчетах обычно применяется энергетический метод. Этот метод решения применим в тех случаях, когда скорость ударяющего тела мала по сравнению со скоростью распространения ударной волны, а время соударения значительно больше времени распространения этой волны по всей системе. Это позволяет считать, что при ударе деформации распространяются мгновенно по всей стержневой системе и все ее точки начинают движение одновременно.

При ударном действии нагрузки различные точки системы получают некоторые скорости, системе придается кинетическая энергия, которая переходит в потенциальную энергию деформации конструкции, а также в другие виды энергии – прежде всего в тепловую.

Техническая (элементарная) теория удара основана на следующих допущениях:

1. Удар считается неупругим, то есть ударяющее тело продолжает двигаться вместе с ударяемой конструкцией, не отрываясь от нее.

2. Ударяемая конструкция имеет лишь одну степень свободы, и вся масса конструкции сосредоточена в точке удара.

3. Вся кинетическая энергия ударяющего тела переходит в потенциальную энергию деформации ударяемой конструкции.

4. Ударяемая конструкция считается идеально упругой. Это означает, что зависимость между динамическими усилиями и перемещениями, следует закону Гука.

Назовем отношение динамических и статических перемещений коэффициентом динамичности или динамическим коэффициентом - , где - динамические и - статические смещения точек ударяемой системы. Тогда в соответствии с законом Гука - , где: , - динамические и статические силовые факторы и реакции в конструкции; , - динамические и статические напряжения.

Коэффициент динамичности при ударе по безмассовой упругой системе.

Вертикальный удар. Предположим, что груз весом падает с некоторой высоты на упругую систему, масса которой мала по сравнению с массой груза. Упругую систему будем считать невесомой. Такой системой может быть стержень, балка, ферма и т. д.

Рассматривая баланс кинетической и потенциальной (энергии упругой деформации) энергий в момент наибольшей деформации системы при ударе, можно получить выражение для коэффициента динамичности

(1.7),

где - статическое смещение точки удара упругой системы под действием силы веса и по ее направлению.

После нахождения , могут быть определены динамические напряжения и деформации системы, которые, очевидно, будут в раз больше тех, которые имели бы место в системе при статическом приложении к ней груза . Заметим, что эластичные свойства системы, как видно из формулы (1.7) смягчают удар и, наоборот, сила удара тем больше, чем больше жесткость системы.

Другой, более общий вид формулы для коэффициента динамичности можно получить, записывая работу веса груза при ударе как сумму: , где - кинетическая энергия груза к моменту удара. Тогда получим выражение:

(1.8).

Выражая кинетическую энергию груза через его скорость и ускорение свободного падения , получим еще один вариант формулы коэффициента динамичности при ударе:

(1.9).

Частный случай ударного нагружения - внезапное приложение груза, когда . В этом случае и , , т. е. при внезапном приложении нагрузки напряжения и деформации системы в два раза больше, чем при статическом нагружении.

Вертикальный удар вследствие внезапной остановки вертикального движения. Удар вследствие внезапной остановки движения возникает, например, в тросе лифта при внезапной остановке кабины или в балке двигающейся со скоростью , на которой закреплен груз .

В этом случае выражение коэффициента динамичности имеет вид:

(1.10).

Горизонтальный удар. Рассмотрим произвольную упругую систему, по которой ударяет груз массы , движущийся в момент удара горизонтально со скоростью . В этом случае сила веса груза перпендикулярна перемещению и работы не совершает. В формуле (1.9) следует оставить только слагаемое, связанное с кинетической энергией груза на момент удара, и коэффициент динамичности определится выражением:

(1.11).

(Здесь - такое перемещение точки удара упругой системы, которое она получила бы в случае статического приложения по направлению удара силы веса груза - ).

Влияние массы ударяемой системы на коэффициент динамичности. В приведенных выше рассуждениях масса ударяемой упругой системы не учитывалась. Учет массы ударяемой системы в технической теории удара всегда приводит к снижению динамических напряжений и деформаций те есть к снижению коэффициента динамичности. Происходит это из-за того, что в момент удара груза по упругой системе, имеющей массу, система в точке удара и груз приобретают одинаковую скорость, которая по закону сохранения импульса будет меньше скорости груза до удара. При этом часть кинетической энергии груза расходуется на местную деформацию ударяемой системы и груза в месте удара.

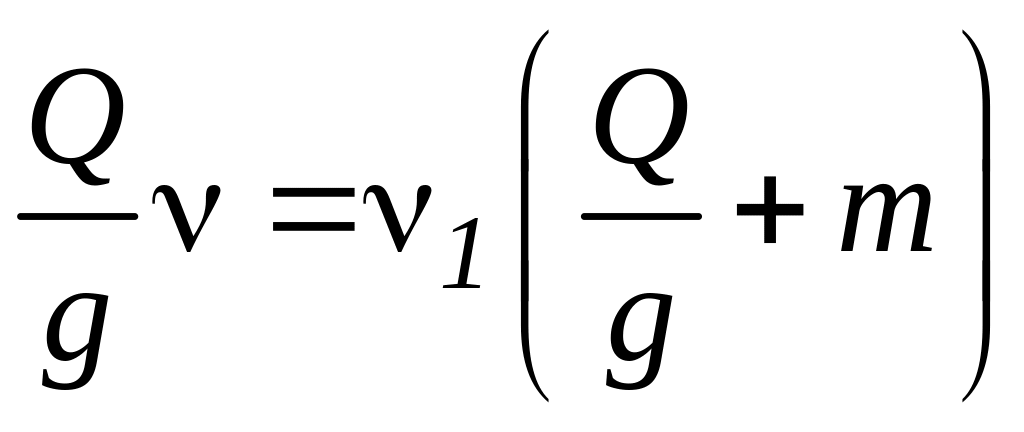
Рассмотрим произвольную упругую систему, с закрепленной в месте удара сосредоточенной массой . В момент соударения груз весом , имеющий до удара скорости и точка удара упругой системы начинают двигаться совместно со скоростью . Величина скорости определяется из теоремы о сохранении количества движения: следовательно, она меньше скорости груза до удара. В этом случае при определении коэффициента динамичности можно пользоваться полученными ранее формулами (1.7-1.11), только вместо скорости груза до удара в них нужно подставить скорость .

В случае, когда необходимо учесть собственную распределенную массу упругой системы ее заменяют условной сосредоточенной массой, которую называют приведенной массой системы. Величина приведенной массы зависит от распределения масс по ударяемой системе и от точки приведения (удара). Условием, из которого определяется величина приведенной массы, является равенство кинетических энергий движения распределенной массы ударяемой системы и приведенной массы после удара. Упрощенно считают, что эпюра скоростей точек ударяемой системы подобна эпюре смещений точек системы при статическом приложении веса груза.