- •1. Теоретическая часть.
- •1.1. Статически неопределимые стержневые системы.
- •1.2. Расчет упругих стержневых систем при колебаниях.
- •1.3. Расчет упругих стержневых конструкций при ударном нагружении.
- •2. Пример выполнения расчетно-проектировочной работы.
- •2.1. Задание.
- •2.2. Порядок решения задачи.
- •2.3. Решение.
- •3. Приложения.
- •3.1. Контрольные вопросы для самоподготовки.
- •3.1.1. Статически неопределимые системы.
- •3.1.2. Динамическое нагружение упругих стержневых систем.
- •164500, Г.Северодвинск, ул. Воронина, д.6
Федеральное агентство по образованию
Филиал «СЕВМАШВТУЗ»
государственного образовательного учреждения высшего
профессионального образования «Санкт-Петербургский государственный морской технический университет» в г. Северодвинске
Лобанов Н.В.
Строительная механика машин
РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМОЙ СТЕРЖНЕВОЙ СИСТЕМЫ ПРИ ДИНАМИЧЕСКОМ НАГРУЖЕНИИ
Учебно-методическое пособие к выполнению расчетно-проектировочной работы для студентов специальности 140200(180103)
Северодвинск
2009
УДК 539.3/.8
Лобанов Н.В.
Строительная механика машин. Расчет статически неопределимой стержневой системы при динамическом нагружении. Учебно-методическое пособие к выполнению расчетно-проектировочной работы.
Северодвинск. Севмашвтуз, 2009.- 43 с.
Учебное пособие содержит подробно разобранный пример выполнения расчетной работы по темам «Статически неопределимые стержневые системы» и «Расчеты стержневых систем при динамическом воздействии» дисциплины «Строительная механика машин», изучаемой студентами специальности 140200(180103). В пособии приводится теоретический материал, необходимый для освоения соответствующих разделов изучаемой дисциплины и самостоятельного выполнения расчетно-проектировочной работы по этим разделам. В конце пособия приведены контрольные вопросы.
Учебное пособие может быть использовано студентами всех специальностей, изучающих дисциплины «Прикладная механика», «Техническая механика» «Сопротивление материалов», в рамках которых выполняются расчетно-проектировочные и контрольные работы по соответствующим темам.
Ответственный редактор: канд. техн. наук, доцент кафедры «Проектирование подъемно-транспортного и технологического оборудования» Севмашвтуза Лобанов Н.В.
Рецензенты: канд. техн. наук, доцент кафедры «Технология металлов и машиностроения» Севмашвтуза Пестов Н. А.;
Лицензия на издательскую деятельность
Код 221. Серия ИД №01734 от 11 мая 2000 года
ISBN 5-7723- СЕВМАШВТУЗ, 2009
Содержание
1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ. 4
4
1.1. Статически неопределимые стержневые системы. 4
1.2. Расчет упругих стержневых систем при колебаниях. 8
1.3. Расчет упругих стержневых конструкций при ударном нагружении. 16
2. ПРИМЕР ВЫПОЛНЕНИЯ РАСЧЕТНО-ПРОЕКТИРОВОЧНОЙ РАБОТЫ. 22
2.1. Задание. 22
2.2. Порядок решения задачи. 23
2.3. Решение. 25
3. ПРИЛОЖЕНИЯ. 37
3.1. Контрольные вопросы для самоподготовки. 37
3.1.1. Статически неопределимые системы. 37
3.1.2. Динамическое нагружение упругих стержневых систем. 38
3.2. Сортамент прокатных профилей 42
3.2.1. Двутавp с уклоном полок по ГОСТ 8239-89 42
3.2.2. Швеллеp с уклоном полок по ГОСТ 8240-89 43
1. Теоретическая часть.
В теоретической части коротко излагаются основные понятия, определения, математические зависимости и правила из соответствующих разделов дисциплин, необходимые для их освоения и выполнения расчетно-проектировочной работы.
1.1. Статически неопределимые стержневые системы.
Статически неопределимыми стержневыми системами называются такие системы, в которых количество неизвестных превышает число уравнений равновесия. Неизвестными могут являться как внутренние силовые факторы в поперечных сечениях, так и внешние силы - реакции связей (опор).
Степень
статической неопределимости.
Степенью статической неопределимости
системы -
![]() называется разность между количеством
неизвестных -
называется разность между количеством
неизвестных -
![]() и числом уравнений равновесия -
и числом уравнений равновесия -
![]() :
:
![]() .
.
Лишние
связи. Числом лишних связей -
![]() называется количество связей, наложенных
сверх необходимых. Необходимыми
называются связи обеспечивающие
неподвижность (неизменяемость) системы
как твердого тела. Лишние связи могут
быть внутренними ограничивающими
взаимные относительные смещения точек
стержневой системы и внешними
ограничивающими абсолютные смещения
точек стержневой системы относительно
неподвижной системы координат. Общее
число лишних связей равно сумме внутренних
лишних -
называется количество связей, наложенных
сверх необходимых. Необходимыми
называются связи обеспечивающие
неподвижность (неизменяемость) системы
как твердого тела. Лишние связи могут
быть внутренними ограничивающими
взаимные относительные смещения точек
стержневой системы и внешними
ограничивающими абсолютные смещения
точек стержневой системы относительно
неподвижной системы координат. Общее
число лишних связей равно сумме внутренних
лишних -
![]() и внешних лишних -
и внешних лишних -
![]() связей:
связей:
![]() .
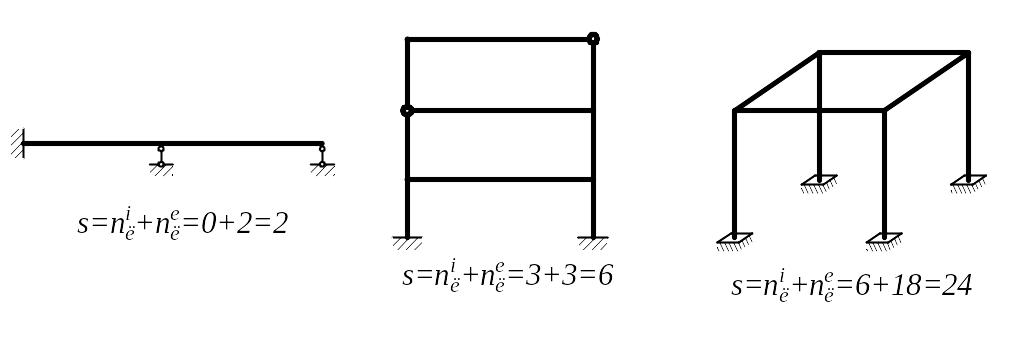
Примеры статически неопределимых
стержневых систем показаны на рис.11.1.
.
Примеры статически неопределимых
стержневых систем показаны на рис.11.1.
|
Рис.1.1 |
Лишние внутренние связи в стержневых системах появляются только при наличии замкнутого контура. Плоский жесткий (без шарниров) замкнутый контур имеет 3 лишние внутренние связи. Пространственный жесткий замкнутый контур дает 6 лишних внутренних связей. Одиночный шарнир, врезанный в плоский замкнутый контур, устраняет одну лишнюю внутреннюю связь. Одиночным или простым шарниром называется шарнир, соединяющий два стержня. Шарнир, соединяющий более двух стержней, называется кратным (соединяющий 3 стержня – двукратным, 4 стержня – трехкратным и т.д.) и эквивалентен числу шарниров равному его кратности. Цилиндрический шарнир, врезанный в пространственный контур, также устраняет одну лишнюю внутреннюю связь.
Важным для анализа статически неопределимых
систем является следующее обстоятельство:
степень статической неопределимости
стержневой системы равна количеству
лишних связей:
![]() .
.
Методы раскрытия статической неопределимости. В случае произвольно нагруженных стержневых систем применяются формализованные методы, в которых дополнительные условия для раскрытия статической неопределимости записаны в виде канонических уравнений. Наибольшее распространение получили два таких метода: метод сил, метод перемещений.
Метод сил. Порядок раскрытия статической неопределимости линейно-упругих стержневых систем по методу сил состоит из нескольких обязательных этапов:
1. Из исходной - раз статически неопределимой системы формируется основная система. Основная система получается из исходной путем отбрасывания лишних связей, следовательно, является статически определимой. (Из исходной, можно получить несколько различных основных систем, но в любом случае основная система должна быть геометрически неизменяемой, то есть неподвижной).
2. Из основной системы формируют статически
определимую эквивалентную систему
(она имеет такие же деформации,
следовательно, и внутренние силы, как
и исходная система). Эквивалентная
система получается добавлением
сил
![]() по направлению отброшенных лишних
связей. Силы
называются лишними неизвестными и
являются реакциями отброшенных связей.
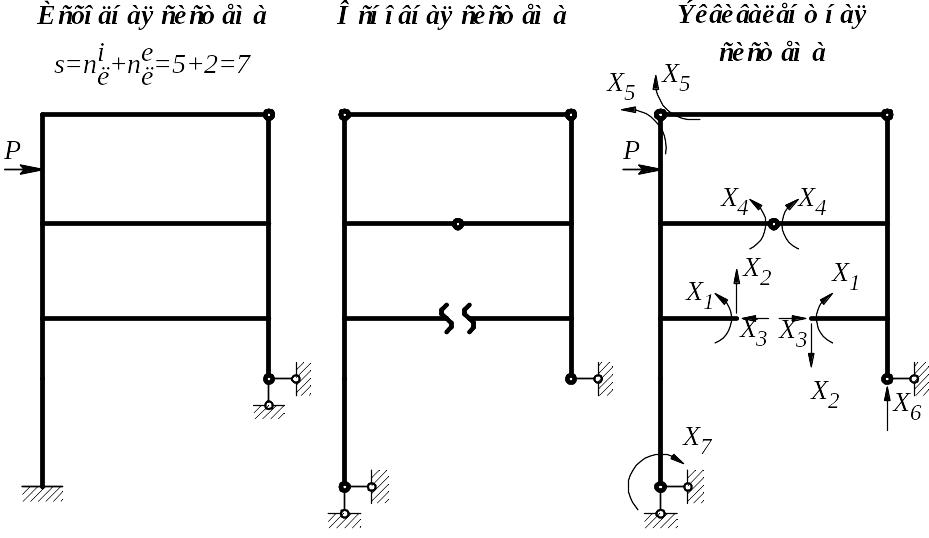
Пример статически неопределимой плоской
рамы со степенью статической неопределимости
-
по направлению отброшенных лишних
связей. Силы
называются лишними неизвестными и
являются реакциями отброшенных связей.
Пример статически неопределимой плоской
рамы со степенью статической неопределимости
-
![]() (лишних
внутренних связей -
(лишних
внутренних связей -
![]() ,
лишних внешних связей -
,
лишних внешних связей -
![]() )
приведен на рис.1.2. Лишние неизвестные,
приложенные вместо отброшенных внутренних
лишних связей, всегда прикладываются
попарно (см. рис.1.2, неизвестные
)
приведен на рис.1.2. Лишние неизвестные,
приложенные вместо отброшенных внутренних
лишних связей, всегда прикладываются
попарно (см. рис.1.2, неизвестные
![]() ),
так как являются силами взаимодействия
двух частей рассматриваемой системы.
),
так как являются силами взаимодействия
двух частей рассматриваемой системы.
3.Величины лишних неизвестных определяются из условий равенства нулю перемещений по направлению отброшенных связей, которые записываются системы канонических уравнений метода сил:
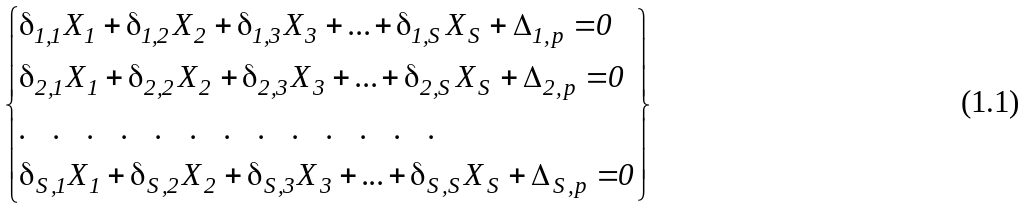
|
Рис.1.2
|
где:
![]() -
перемещение по направлению
-
перемещение по направлению
![]() -
той отброшенной связи, вызванное
действием единичной нагрузки приложенной
по направлению
-
той отброшенной связи, вызванное
действием единичной нагрузки приложенной
по направлению
![]() -
той связи (т.е.
-
той связи (т.е.
![]() );
);
![]() -
перемещение по направлению
-
той отброшенной связи вызванное действием
внешней нагрузки,
-
перемещение по направлению
-
той отброшенной связи вызванное действием
внешней нагрузки,
![]() .
На основании теоремы Бетти матрица
коэффициентов системы канонических
уравнений симметрична, то есть:
.
На основании теоремы Бетти матрица
коэффициентов системы канонических
уравнений симметрична, то есть:
![]() ,
что позволяет существенно упростить
решение задачи в случае систем с большой
степенью статической неопределимости.
,
что позволяет существенно упростить
решение задачи в случае систем с большой
степенью статической неопределимости.
Коэффициенты системы канонических уравнений можно находить любым способом, но обычно используется энергетический метод в виде интеграла Мора.
После того как определены неизвестные , вместо исходной статически неопределимой системы можно рассматривать статически определимую эквивалентную систему, перемещения и напряжения, в которой находятся известными методами.