Федеральное агентство по образованию
Государственное образовательное учреждение
«Сибирский федеральный университет»
Институт Фундаментальной Подготовки
Э.В.Березина, л.В.Климович теория вероятностей и математическая статистика
Методические указания для самостоятельной работы
Красноярск, 2008
Введение
Глава 1. Теория вероятностей
1.1. Законы распределения случайных величин
1.1.1. Законы распределения дискретных случайных величин
1.1.1.1. Биноминальное распределение.
1.1.1.2. Распределение Пуассона.
1.1.2. Законы распределения непрерывных случайных величин
1.1.2.1. Равномерное распределение
1.1.2.2. Показательное распределение.
1.1.2.3. Нормальный закон распределения.
1.2. Предельные теоремы теории вероятностей
1.2.1. Закон больших чисел
1.2.2. Центральная предельная теорема
1.3. Система двух случайных величин
Глава 2. Математическая статистика
2.1. Самостоятельная работа по лекционному курсу
2.2. Самостоятельная работа по практическим занятиям
Вопросы для самоконтроля
Список литературы
ПРИЛОЖЕНИЯ
Введение
Развивающая форма организации учебной деятельности ориентирована на самообучение, на самостоятельную работу обучающегося. Это обусловлено требованием к быстрому обновлению научно-технических знаний. В контексте самообучения необходимо:
- самостоятельно приобретать знания, используя различные источники информации;
- обрабатывать полученную информацию;
- выбирать различные способы познавательной деятельности, соответствующие целям и задачам обучения;
- применять полученные и усвоенные знания в ходе решения различных социально-значимых и профессиональных задач и проблем;
- уметь формулировать вопросы для уточнения непонятных частей изучаемого материала.
Самостоятельная работа в структуре образовательного процесса включает в себя: внеаудиторное изучение литературы по предмету, систематическую и целенаправленную деятельность в ходе обязательных учебных занятий, творческую самостоятельную работу под руководством преподавателя.
Целью настоящих методических указаний является помощь обучаемым в организации более углубленного и расширенного изучения теоретического материала раздела «Теория вероятностей и математическая статистика».
Для успешного выполнения самостоятельной работы по теме «Теория вероятностей и математическая статистика» необходимо изучить лекции 8.1–8.8 и разобрать решение заданий учебного пособия «Теория вероятностей и математическая статистика». Для закрепления материала целесообразно решить задания для самостоятельного решения, предложенные в учебном пособии «Теория вероятностей и математическая статистика».
Методические указания написаны в соответствии с программой данной дисциплины и включают в себя две части:
- «Теория вероятностей»,
- «Математическая статистика».
Глава 1. Теория вероятностей
1.1. Приближенные формулы в схеме Бернулли
Данная тема изложена в пункте 8.4.4. электронного конспекта лекций. В результате изучения данной темы студент должен научиться применять ту или иную приближенную формулу в зависимости от условия задачи
Формула Пуассона:
(1.1)
Формулу (1.1) применяют, когда вероятность p успеха (р = const) крайне мала, т. е. сам по себе успех (появление события А) является редким событием, но количество испытаний n велико, среднее число успехов nр=λ незначительно. Приближенную формулу (1.1) обычно используют, когда n≥50, а nр≤10.
Пример 1. Завод «Золотая балка» (Крым) отправил в Москву 1500 бутылок вина. Вероятность того, что в пути одна из бутылок может разбиться, равна 0,002. Найти вероятность того, что в пути будет разбито не более четырех бутылок (событие А).
Решение.
Так как
и
применяется формула Пуассона. Искомая
вероятность равна
Так как n = 1500, p = 0,002, то λ=np=3. Вероятность события А найдем, используя формулу Пуассона (1.1):
В тех случаях,
когда
и вероятность р
наступления
события А в
каждом испытании постоянна и отлична
от нуля и единицы, применяется формула,
полученная в локальной теореме
Муавра-Лапласа:
, (1.2)
где
.
Функция
называется функцией
Гаусса и
имеет вид:
.
График этой функции называют кривой вероятностей (рис. 1.1).
Рис. 1.1
Для функции φ(x) составлены таблицы значений (см. табл.1 приложения). При использовании таблицы следует учитывать, что:
– функция
φ(x)
- четная,
т.е.
;
– при
x ≥
4 можно считать, что
.
Пример 2. Вероятность попадания в мишень при одном выстреле для данного стрелка равна 0,7. Найти вероятность того, что при 200 выстрелах мишень будет поражена 160 раз.
Решение. Здесь
n=200,
р=0,7,
q=0,3,
k=160.
Так как
,
применим формулу (1.2). Имеем:
,
следовательно,
.
По таблице 1
приложения находим
.
Таким образом, искомая вероятность:
.
В тех случаях,
когда требуется вычислить вероятность
того, что в n
независимых
испытаниях событие А
появится не
менее k1,
но не более k2
раз, т.е.
,
используют
интегральную теорему Муавра-Лапласа.
Теорема является частным случаем более
общей теоремы — центральной предельной
теоремы. По интегральной теореме
Муавра-Лапласа вероятность находят
следующим образом:
,
(1.3)
где
,
.
Функция
,
называемая нормированной
функцией Лапласа,
определяется формулой:
, (1.4)
Функция
- нечетная, то есть
;
при
можно считать, что
.
График функции
приведен на рис. 1.2.
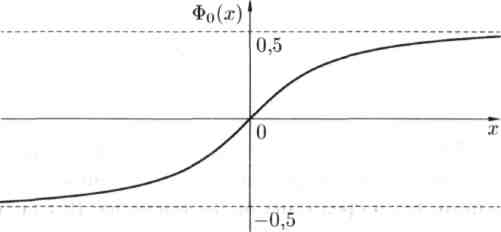
Рис. 1.2
Наряду с нормированной функцией Лапласа (1.4) используют функцию
(1.5)
называемую, также функцией Лапласа. Она связана с функцией формулой
(1.6)
Имеются таблицы
приближенных значений функций
и
(интеграл не берется в элементарных
функциях), которые приводятся в большинстве
учебников по теории вероятностей.
Приближенную формулу для вычисления вероятности можно записать так же в виде
, (1.7)
где ,
Пример 3. Проверкой установлено, что цех в среднем выпускает 96% продукции высшего сорта. На базе приемщик проверяет 200 изделий этого цеха. Если среди них окажется более 10 изделий не высшего сорта, то вся партия изделий бракуется, т. е. возвращается в цех. Какова вероятность того, что партия будет принята?
Решение. Здесь
,
(вероятность
негодного изделия),
.
Вероятность принятия всей партии, т.е.
,
можно найти по формуле (1.3),
,
.
Находим, что
,
.
С помощью функции
Лапласа можно найти вероятность
отклонения относительной частоты
от вероятности р
в n
независимых
испытаниях. Имеет место формула
,
где ε >0.
Пример 4. Вероятность попадания в цель при одном выстреле равна 0,6. Найти вероятность того, что при n = 1200 независимых выстрелах отклонение относительной частоты от вероятности по модулю не превышает ε = 0,05.
Решение.
.
1.2. Законы распределения случайных величин
При выполнении задания этого пункта необходимо демонстрировать понимания различий между дискретной и непрерывной случайными величинами и делать выводы о законах их распределения.
Напомним основные законы распределения дискретных и непрерывных случайных величин.
1.2.1. Законы распределения дискретных случайных величин
1.2.1.1. Биноминальное распределение.
Дискретная случайная величина Х называется распределенной по биномиальному закону, если ее возможные значения 0, 1, ..., n, а вероятность того, что Х=k, выражается формулой
где 0<p<1;
q=1-p.
Параметры распределения n и p.
Математическое
ожидание биномиального закона
распределения
,
дисперсия
,
а среднее квадратичное
.
1.2.1.2. Распределение Пуассона.
Дискретная случайная величина Х называется распределенной по закону Пуассона, если ее возможные значения 0, 1, 2, ... n, ..., а вероятность того, что Х=k, выражается формулой:
(1.8)
где λ=np > 0 – параметр закона Пуассона.
Если известны числа и k, то значения вероятности можно найти по соответствующим таблицам распределения Пуассона.
Числовые характеристики распределения Пуассона:
;
;
.
Таким образом, математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, совпадают и равны параметру этого распределения λ.
Пример 4. В партии 10% нестандартных деталей. Наугад отобраны 4 детали. Написать закон распределения дискретной случайной величины Х – числа нестандартных деталей среди четырех.
Решение. Вероятность появления нестандартной детали в каждом случае равна 0,1.
Найдем вероятности того, что среди отобранных деталей:
а) вообще нет нестандартных деталей
;
б) одна нестандартная деталь
;
в) две нестандартные детали
;
г) три нестандартные детали
;
д) четыре нестандартных детали
.
Запишем закон распределения (табл. 1.1).
Таблица 1.1.
X |
0 |
1 |
2 |
3 |
4 |
P |
0,6561 |
0,2916 |
0,0486 |
0,0036 |
0,0001 |