Планы практических занятий

Практическое занятие № 1. Тема 1. Основания математики

Теория множеств. Основные понятия теории множеств. Основные операции над множествами. Аксиомы алгебры множеств. Диаграммы Венна-Эйлера.

Практическая часть занятия: решение задач.

Примерные задания на операции над множествами.

Для заданных множеств А и В найти АUВ, А∩В, А\В, если А={2, 4, 6}, В={-2, 2, 8,10}.

Для заданных множеств А и В найти , В\А, если А=[-4,4], В= (-∞, 0).

Примерные задания на диаграммы Венна-Эйлера.

Пусть А и В - множества, изображенные на рисунке:

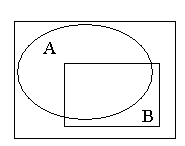
Найти геометрически объединение, пересечение, разность этих множеств.

Рекомендуемая литература:

1. Богатов Д.Ф., Богатов Ф.Г. Конспект лекций и практикум по математике для юристов: учебное пособие. – М. : Приор-издат, 2003. (С. 39-48).

2. Крахин А.В. Математика для юристов: Учебное пособие. – М.: Флинта, 2005. (С. 13-20).

3. Математика для юристов: обучающий видеокурс [Электронный ресурс], 2009. – Режим доступа: http://www.TeachVideo.ru (Урок 81).

4. Попов, А.М., Сотников В.Н., Е.И. Нагаева. Информатика и математика для юристов: учебник / Под ред. проф. А.М. Попова.– М.: Юнити-Дана, 2009. (С. 10-21).

Практическое занятие № 2. Тема 1. Основания математики

Элементы математической логики. Начала алгебры высказываний. Операции над высказываниями. Аксиомы математической логики. Основные логические операции. Элементы математической логики. Начала алгебры высказываний. Операции над высказываниями. Аксиомы математической логики. Основные логические операции. Элементы комбинаторики. Комбинаторные задачи и методы их решения.

Практическая часть занятия: решение задач.

Пример задания на расчет числа перестановок. На огневой рубеж вызывают 8 курсантов. Сколькими способами можно расставить их на огневом рубеже?

Пример задания на расчет числа размещений. Группа курсантов в течение недели осуществляет дежурство на 8 различных объектах академии. Сколькими способами можно составить расписание дежурств в субботу, если в этот день недели должно осуществляться дежурство только на 3-х любых объектах академии.

Пример задания на расчет числа сочетаний. В группе 20 юношей и 10 девушек. Сколькими способами можно избрать 3 юношей и 2 девушек для участия в конференции.

Рекомендуемая литература:

1. Богатов Д.Ф., Богатов Ф.Г. Конспект лекций и практикум по математике для юристов: учебное пособие.– М.:Приор-издат, 2003. (С.74-78).

2. Крахин А.В. Математика для юристов: Учебное пособие. – М.: Флинта, 2005. (С. 20-25).

3. Математика для юристов: обучающий видеокурс [Электронный ресурс], 2009. – Режим доступа: http://www.TeachVideo.ru (Уроки 20-27).

4. Попов, А.М., Сотников В.Н., Е.И. Нагаева. Информатика и математика для юристов: учебник / Под ред. проф. А.М. Попова.– М.: Юнити-Дана, 2009. (С. 32-58, 90-94).

Практическое занятие № 3. Тема 2. Числа и функции

Натуральные, целые и рациональные числа. Десятичные дроби и вещественные числа. Округление дробей. Проценты. Позиционные системы счисления. Правила перевода чисел из одной системы исчисления в другую.

Практическая часть занятия: решение задач.

Пример задания на простые проценты. На территории n-го УВД в мае было совершено 320 правонарушений. В июне правонарушения составили 110% от мая. Сколько правонарушений было в июне?

Пример задания на вычисление сложных процентов. Группа экспертов по плану должна исследовать 360 сторублевых купюр. В первые 8 дней они перевыполняли задание на 20 %. В оставшиеся дни группа экспертов смогла дополнительно исследовать 82 купюры того же достоинства. Сколько дней работала группа экспертов.

Рекомендуемая литература:

1. Богатов Д.Ф., Богатов Ф.Г. Конспект лекций и практикум по математике для юристов: учебное пособие. – М. : Приор-издат, 2003. (С. 51-66).

2. Крахин А.В. Математика для юристов: Учебное пособие. – М.: Флинта, 2005. (С. 25-26).

3. Математика для юристов: обучающий видеокурс [Электронный ресурс], 2009. – Режим доступа: http://www.TeachVideo.ru (Урок 81).

Практическое занятие № 4. Тема 2. Числа и функции

Понятие функции. Способы задания функции. Свойства функций. Сложная функция. Аппроксимация, интерполяция функций. Предел функции. Правила вычисления пределов.

Практическая часть занятия: решение задач.

Пример задания на область определения функции. Найти область определения функции

Пример задания на графическое представление функций. Построить график функции у= 5х² + 3х – 5.

Пример задания на различные виды графического представления функций. Представить данные невыплаты налогов предпринимателями в городе N по данным таблицы в виде столбчатой и секторной диаграмм.

Рекомендуемая литература:

1. Богатов Д.Ф., Богатов Ф.Г. Конспект лекций и практикум по математике для юристов: учебное пособие. – М. : Приор-издат, 2003. (С. 91-113).

2. Крахин А.В. Математика для юристов: Учебное пособие. – М.: Флинта, 2005. (С. 29-35).

3. Математика для юристов: обучающий видеокурс [Электронный ресурс], 2009. – Режим доступа: http://www.TeachVideo.ru (Урок 14, уроки 44-57).

Практическое занятие № 5. Тема 3. Элементы теории вероятностей

Основные понятия теории вероятностей. Частота и вероятность. Классификация событий. Противоположные события. Теорема сложения вероятностей несовместных событий. Теорема сложения вероятностей совместных событий. Теорема умножения вероятностей независимых событий. Теорема умножения вероятностей зависимых событий.

Практическая часть занятия: решение задач.

Пример задания на вычисление вероятности простого события. В учебной практике из 25 студентов: 5 – отличники, 20 – хорошисты. Какова вероятность, что наугад вызванный студент является отличником?

Пример задания на вычисление вероятностей совместных событий. В учебной группе 2 курсанта сдают экзамен по математике. Вероятность сдачи экзамена первым курсантом равна 0,6, а вторым курсантом – 0,4. Какова вероятность того, что экзамен сдаст хотя бы один курсант?

Пример задания на вычисление вероятностей зависимых событий. Группа экспертов дактилоскопического учета выполняет работу по реконструкции отпечатков фаланг пальцев рук, поступающих с мест нераскрытых преступлений. Результат работы этой группы – 75 % из поступивших на экспертизу отпечатков являются годными и условно пригодными для дальнейшего исследования (событие А). Также известно, что годными для последующей обработки отпечатков (событие В) получаются 55 из 100. Определить вероятность того, что произвольно взятый отпечаток будет использован в дальнейшей работе и что он является годным.

Рекомендуемая литература:

1. Богатов Д.Ф., Богатов Ф.Г. Конспект лекций и практикум по математике для юристов: учебное пособие. – М. : Приор-издат, 2003. (С. 152-186).

2. Крахин А.В. Математика для юристов: Учебное пособие. – М.: Флинта, 2005. (С. 66-80).

3. Математика для юристов: обучающий видеокурс [Электронный ресурс], 2009. – Режим доступа: http://www.TeachVideo.ru (Уроки 28-43).

4. Попов, А.М., Сотников В.Н., Е.И. Нагаева. Информатика и математика для юристов: учебник / Под ред. проф. А.М. Попова.– М.: Юнити-Дана, 2009. (С. 84-90, 94-101).

Практическое занятие № 6. Тема 3. Элементы теории вероятностей

Условная вероятность. Вероятность выявления хотя бы одного события. Формула полной вероятности. Формула Бейеса. Формула Бернулли. Закон распределения дискретной случайной величины. Непрерывные случайные величины. Нормальный закон распределения. Математическое ожидание и дисперсия.

Практическая часть занятия: решение задач.

Пример задания на условную вероятность. Три группы ГИБДД МВД России по 3-м независимым направлениям осуществляют поиск одного из 3-х угнанных автомобилей. Вероятность того, что первая группа обнаружит автомобиль, равна 0,5, вторая – 0,6, третья – 0,8. Найти вероятность следующих событий: А – будут обнаружены все 3 автомобиля; В – первая группа не обнаружит автомобиля, а вторая и третья – обнаружат; С – первая и вторая группа не обнаружат автомобиль, а третья – обнаружит.

Пример задания на определение основных статистических характеристик. Имеются табличные ежемесячные данные о правонарушениях подростков на территории n-го УВД за год. Вычислить математическое ожидание (среднее значение) и дисперсию (вариацию по месяцам).

Рекомендуемая литература:

1. Богатов Д.Ф., Богатов Ф.Г. Конспект лекций и практикум по математике для юристов: учебное пособие. – М. : Приор-издат, 2003. (С. 170-184).

2. Крахин А.В. Математика для юристов: Учебное пособие. – М.: Флинта, 2005. (С. 73-91).

3. Математика для юристов: обучающий видеокурс [Электронный ресурс], 2009. – Режим доступа: http://www.TeachVideo.ru (Уроки 28-43).

4. Попов, А.М., Сотников В.Н., Е.И. Нагаева. Информатика и математика для юристов: учебник / Под ред. проф. А.М. Попова.– М.: Юнити-Дана, 2009. (С. 113-126).

Практическое занятие № 7. Тема 4. Основы математической статистики

Предмет математической статистики. Основные задачи математической статистики. Статистические ряды распределений. Выборка. Группировка статистических данных. Описательные статистики. Средние величины. Вычисление средней арифметической в рядах распределения. Среднее геометрическое. Средняя гармоническая. Вычисление структурных средних. Вычисление медианы. Вычисление моды.

Практическая часть занятия: решение задач.

Пример задания на метод группировки. По данным ГИАЦ МВД России, состояние тяжких и особо тяжких преступлений за отчетный период по 26 регионам России приведено в таблице. Провести анализ состояния преступности по регионам, применяя метод группировок.

Пример задания на закон распределения. По 22 подследственным имеются данные о числе членов в их семьях. Построить дискретный вариационный ряд и проанализировать характер распределения семей по числу членов в них. Представить результаты графически.

Пример задания на вычисление средних. В сводке приведены сведения о количестве гражданских дел по ответственности за нарушение обязательств в суде, а также сведения об общей сумме всех исков с января по июнь. Определить, какая сумма денег приходится в среднем на одно дело.

Рекомендуемая литература:

1. Богатов Д.Ф., Богатов Ф.Г. Конспект лекций и практикум по математике для юристов: учебное пособие. – М. : Приор-издат, 2003. – (С. 245-271).

2. Крахин А.В. Математика для юристов: Учебное пособие. – М.: Флинта, 2005. (С. 92-113).

3. Математика для юристов: обучающий видеокурс [Электронный ресурс], 2009. – Режим доступа: http://www.TeachVideo.ru (Уроки 15-19).

4. Попов, А.М., Сотников В.Н., Е.И. Нагаева. Информатика и математика для юристов: учебник / Под ред. проф. А.М. Попова.– М.: Юнити-Дана, 2009. (С. 167-182).

5. Правовая статистика: учебник / Под ред. проф. С.Я. Казанцева, проф. С.Я. Лебедева. – М.: Юнити, 2008. (С. 32; С. 42-57).

Практическое занятие № 8. Тема 4. Основы математической статистики

Показатели вариации: дисперсия и стандартное отклонение. Ряды динамики. Взаимосвязи исследуемых явлений в социально-правовой сфере.

Практическая часть занятия: решение задач.

Пример задания на обработку динамических рядов. Имеются табличные данные, характеризующие движение числа гражданских дел в районном суде за 7 месяцев. Определить начальный, конечный и средний уровни ряда, длину ряда. Охарактеризовать ряд. Провести преобразование динамического ряда путем его сглаживания. Сделать выводы о наличии или отсутствии тенденций.

Пример задания на выявление взаимосвязей исследуемых явлений. Данные о количестве курсантов, опоздавших на занятия в течение контрольного времени, представлены в виде таблицы, где х – время опоздания в минутах, у – число опоздавших. Вычислить парный коэффициент корреляции, построить график связи между х и у, определить по нему уравнение линейной связи между количеством опоздавших курсантов и временем опоздания.

Рекомендуемая литература:

1. Богатов Д.Ф., Богатов Ф.Г. Конспект лекций и практикум по математике для юристов: учебное пособие. – М. : Приор-издат, 2003. (С. 81-137).

2. Крахин А.В. Математика для юристов: Учебное пособие. – М.: Флинта, 2005. (С. 114-128).

3. Математика для юристов: обучающий видеокурс [Электронный ресурс], 2009. – Режим доступа: http://www.TeachVideo.ru (Уроки 19, 58).

4. Правовая статистика: учебник / Под ред. проф. С.Я. Казанцева, проф. С.Я. Лебедева. – М.: Юнити, 2008. (С. 81-137).

Практическое занятие № 9. Тема 5. Общие вопросы статистических исследований в юридической деятельности.¹

Общие вопросы статистических исследований. Программно-методологические и организационные вопросы статистического исследования. План выборки – научный метод статистических исследований. Основные понятия в статистических исследованиях. Формирование информационной базы статистических исследований. Система учетов органов внутренних дел. Этапы статистического исследования.

Практическая часть занятия состоит в тестировании по основным понятиям и терминологии (объем тестового задания – 60 вопросов по всем разделам правовой статистики).