Часть 2. Краевая задача для обыкновенного дифференциального уравнения 2-го порядка.

В общем виде имеем задачу:

, , .

Кроме уравнения задаются 2 дополнительных условия на концах промежутка . Эти условия называются краевыми или граничными и имеют вид

Рассмотрим случай, когда функции линейные относительно .

§ 5. Метод разностной прогонки для обыкновенных дифференциальных уравнений.

Будем предполагать, что эта задача имеет единственное решение y(x), обладающее необходимой гладкостью. Пусть — достаточно гладкие функции, — заданные константы. Рассмотрим метод сеток применительно к этой задаче.

Будем искать приближенные значения функции y(x) на некоторой заданной системе точек— сетке узлов.

1. Построим на отрезке [a , b] некоторую систему точек .

2. Заменим входящие в задачу производные разностными отношениями по значениям функций в этих точках. После этого задача сведется к системе линейных алгебраических уравнений, в которой неизвестными будут значения решения .

3. Решим полученную систему каким-либо известным методом.

4. Установим соответствие между полученным решением в точках и искомым непрерывным решением.

Рассмотрим задачу ( 5.1 ). На [a,b] построим равномерную сетку узлов: , (5.2)

n —целое. — узлы сетки.

введем обозначения:

Через обозначим приближенное решение задачи в точке .

Заменим входящие в дифференциальное уравнение производные разностными отношениями:

(5.3)

Заметим, что погрешность, с которой мы заменяем эти производные, является величиной порядка . (имеется в виду разность между точным значением производных в точке и величинами, полученными по формулам, стоящим справа при точных вычислениях).

В граничные условия тоже входят 1-е производные в точках a и b. Для замены этих производных разностными отношениями можно использовать различные способы. Для начала мы воспользуемся односторонними разностными выражениями 1-го порядка:

(5.4)

В результате этой замены мы получим систему линейных алгебраических уравнений:

Перепишем систему в виде:

(5.6)

Это система с трехдиагональной матрицей.

Для решения такой системы применим метод прогонки.

Решение этой системы будем искать в виде:

i=0,1,2,...,n-1 (5.7)

В этой формуле коэффициенты пока не определены.

Из 1-го уравнения системы (5.6) получаем

Последующие коэффициенты находим с помощью рекуррентных соотношений.

, исключим

(5.8)

Из последнего уравнения системы и соотношения (5.8) для , находим

Отсюда

Затем по формулам (5.7) находим

Заметим, что формулы (5.3) содержат ошибку порядка h² , в то время как формулы (5.4) содержат ошибку порядка h. Можно увеличить порядок точности за счет более точной замены входящих в граничные условия производных разностными отношениями более высокого порядка точности. Один из способов состоит в применении трехточечных односторонних разностных производных 2-го порядка точности:

. (5.9)

Теперь вместо 0-го и последнего уравнений в системе (5.5) мы получим выражения

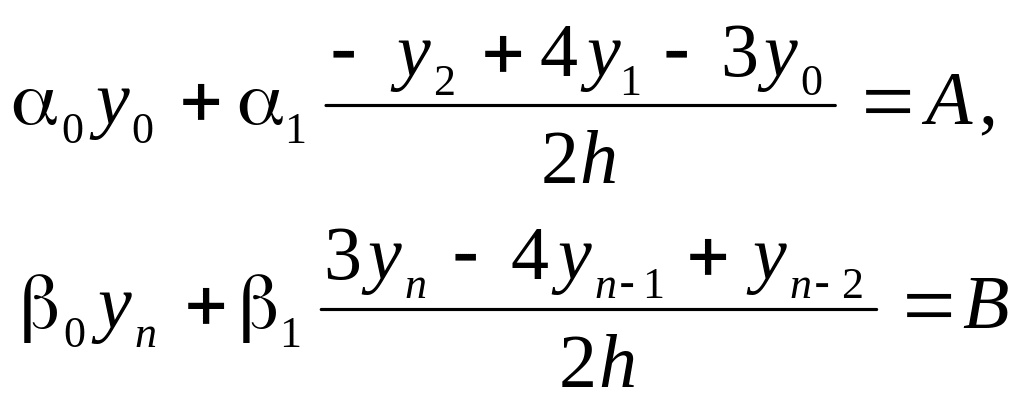
Если мы из левого граничного условия и 1-го уравнения исключим , а из правого граничного условия и последнего уравнения исключим , то получим обычную трехдиагональную систему :

Для системы (5.6) должны быть выполнены условия :

i = 0, . . . , n . Эти условия будут выполнены, если, например, ,

Если же не является тождественным нулем (в уравнении присутствует 1-я производная), то нужно добавить условие при всех i, которое будет выполняться, если соответствующим образом выбрать h.