10

Лекция 11.

Глава 4. Решение обыкновенных дифференциальных уравнений

(1)

Часть 1.

Задача Коши:

(2)

— заданные значения.

Задача Коши для обыкновенного дифференциального уравнения 1-го порядка.

(3)

Теорема 1 (Пикар). Пусть

непрерывна по x и y , удовлетворяет условию Липшица по у :

и

в S .Тогда задача (3) имеет единственное решение на отрезке , где и график решения лежит в S.

§ 1. Разложение в ряд Тейлора в окрестности точки .

₍₃₎

Теорема 2 (Коши). Пусть ,как функция от двух переменных разлагается в ряд Тейлора в окрестности точки :

,

. Тогда задача (3) имеет решение , представимое в виде ряда

, (1.1)

сходящегося в некоторой окрестности точки .

Можно указать и окрестность. Пусть М — такая постоянная, что в окрестности .

Тогда ряд (1.1) сходится при , где

.

Перепишем ряд (1.1) в виде

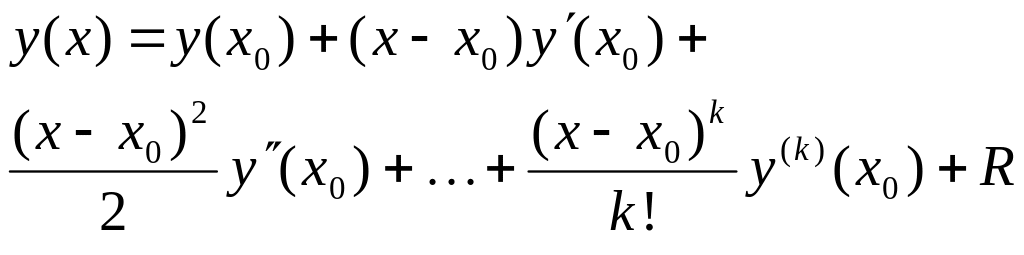(1.2)

По этой формуле можно последовательно вычислять значения в точках если известны значения .

Строим отрезок ряда (1.2)

. (1.3)

—дано,

— получаем из уравнения,

и т.д.

Берем последовательность точек ,

h — малое число, и по (1.3) вычисляем . Нужно выбирать число k таким образом, чтобы остаточный член

(1.4)

для всех не превосходил по абсолютной величине некоторое число, определяющее заданную точность вычислений .

З а м е ч а н и е . Метод очень громоздкий и позволяет находить решение только вблизи точки .

§ 2. Метод Эйлера.

или

(2.1)

, где — некоторый малый шаг. , где .

Значение можно считать приближенным для .

и вычислим

, где .

И так далее. Для получим

, где .…....(2.2)

Решение — последовательность значений в точках . В каждой точке можно построить решение , зная только решение в точке . Это метод Эйлера. Такой метод называется одношаговым. Можно получать значения решения и в точках .

Об ошибке метода Эйлера. Сначала определим ошибку на одном шаге при условии, что предыдущее значение вычислено точно. Пусть — ошибка 1-го шага, . Тогда .

.

Разложим в ряд в окрестности точки . Отсюда . Это локальная ошибка.

Через число шагов, пропорциональное величине 1/h , ошибка будет

. Это глобальная ошибка.

Порядком метода называется показатель степени при h в глобальной ошибке.

Порядок метода Эйлера равен 1. (можно также определить порядок метода как показатель степени при h в локальной ошибке, уменьшенный на 1 )

Можно построить метод, аналогичный методу Эйлера, но 2-го порядка. Он называется улучшенный метод Эйлера:

(2.3)

Проверим, что порядок равен 2.

Отсюда . Значит, порядок метода —2-й.

Неустойчивость метода Эйлера.

Решение — функция , проходящая через точку . Выражение означает,что — точка на касательной . Т.е. На каждом шаге метода Эйлера мы переходим на другую интегральную кривую.