Министерство общего и профессионального образования

Российской федерации

ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

МАТЕМАТИЧЕСКИЙ ФАКУЛЬТЕТ

КАФЕДРА МАТЕМАТИЧЕСКОГО АНАЛИЗА

919

Первая и вторая теоремы Н.Н. Боголюбова – Н.М. Крылова в принципе

устреднения

Составитель М.И. Каменский

Воронеж 1998

Начиная с появившихся о конце 60-х начале 70-х годов работ Л.М.Самойленко [10], В.В. Стрыгина [11], Р.Р. Ахмерова и М.И. Каменского [1] и др., стала понятна связь классических теорем Н.Н. Боголюбова – Н.М. Крылова в принципе усреднения с теорией топологического индекса [2] (теорией вращения векторных полей [7]). В указанных теоремах топологический индекс решения усредненного уравнения оказывается отличным от нуля, что позволяет получать их как следствие общих результатов о непрерывной зависимости от параметра решений операторных уравнений с вполне непрерывными операторами. При этом удается снять многие чисто технические условия типа дифференцируемости правой части в принципе усреднения для начальной задачи или невырожденности матрицы, полученной в результате линеаризации правой части усредненного уравнения, в задаче о периодических решениях. Такой взгляд на принцип усреднения в дальнейшем получил широкое развитие и применялся для различных уравнений(см., например,[4-6,9-11]). Однако в монографической литературе он практически не излагается.

Настоящее пособие дает возможность студентам математических специальностей университетов получить представление о принципе усреднения и методах его обоснования с помощью теории топологического индекса. Пособие написано на основе спецкурса,читавшегося кандидатам в магистры на кафедре математического анализа Воронежского госуниверситета в 1996/97 уч. году. Излагаемый материал предполагает знание студентами основ математического анализа и обыкновенных дифференциальных уравнений. Пособие может бытьиспользовано, начиняя с третьего курса обучения.

§1. Теория топологического индекса вполне непрерывных операторов.

Через 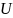обозначается открытое ограниченное множество банаховапространства 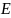. Через – егограница и замыкание соответственно. Всюду ниже – вполне непрерывный оператор.

1. Допустимые гомотопии. Два вполне непрерывных оператора

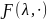называются гомотопными, если существует вполне непрерывный по совокупности переменных оператор , такой что , и не имеет неподвижных точек на при .

Гомотопия называется линейной, если она задается формулой:

.

1.2. Индекс множества неподвижных точек вполне непрерывного оператора. Если вполне непрерывный оператор не имеет неподвижных точек на границе , то определена целочисленная характеристика, называемая индексом множества неподвижных точек оператора и обозначаемая , со следующими свойствами:

1 . Индексы гомотопных вполне непрерывных операторов совпадают.

2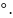 Пусть , 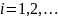попарно непересекающиеся открытые подмножества 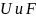не имеют неподвижных точек в Тогда величины определены для всех i, только дляконечного числа из них отличны он нуля и

3 . Если

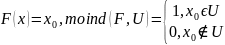
4 Если то оператор имеет по крайней мере одну неподвижную точку в

Если изолированная неподвижная точка оператора 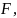т.е. в некотором шаре у оператора нет других неподвижных точек, то индексом называют величину , при .

Индексом точки обозначают .

1.3. Теорема о сужении. Пусть L замкнутое выпуклое подмножество пространства E и

Не имеет неподвижный точек н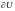а . Тогда

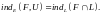
1.4. Теорема о вычислении индекса по линейной части. Пусть вполне непрерывный оператор F, действующий в банаховом пространстве E, определен в некоторой окрестности своей неподвижной точки и дифференцируем по Фреше в точке . Пусть 1 не является собственным значением линейного оператора

Тогда является изолированной неподвижной точкой оператора F и 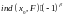, где β-сумма кратностей вещественных больших единицы собственных значений оператора

§2. Классические первая и вторая теоремы н.И. Боголюбова – н.М. Крылова с формулировкой условий в терминах топологического индекса.

Опишем обобщения классических теорем Н.И. Боголюбова – Н.М. Крылова (см. (3)), получающиеся при применении теории топологического индекса.

Рассмотрим систему обыкновенных дифференциальных уравнений

,

(1)

где 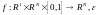-положительный параметр. Предположим, что

(2)

Принцип усреднения заключается в оценке близости решений системы (1) к решениям обычно более простой автономной системы

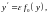
(3)

где

(4)

Рассмотрим задачу Коши. Пусть решения 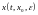и систем (1) и (3) удовлетворяют одинаковому начальному условию

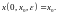
(5)

(6)

Перед формулировкой теоремы напомним, интегральной воронкой решений системы дифференциальных уравнений называют множество ее решений, удовлетворяющих одному и тому же начальному условию.

2.1. Теорема. Пусть оператор непрерывен по совокупности переменных и интегральная воронка системы (3) с начальным условием (6) при 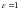ограничена на отрезке .

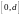Тогда каждому соответствует такое , что при на отрезке интегральная воронка ограничена и для любого решения системы (1) с начальным условием (5) существует решение системы (3) с начальным условием (6) такое, что

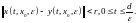
(7)

Когда интегральная воронка задачи (3),(6) при состоит из одного решения, то теорема 2.1 превращается в следующее утверждение.

2.2 Следствие. Пусть оператор непрерывен по совокупности переменных и система (3) с начальным условием (6) при имеет единственное решение на отрезке .

Тогда каждому соответствует такое , что при верна оценка

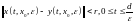
(8)

2.3. Замечание. В теореме 2.1.1 и следствии 2.1.2 требование непрерывности оператора можно заменить менее ограничительным требованием непрерывности лишь на

(9)

Где 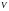- некоторая окрестность множества

.

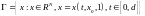2.4. Замечание. Аналогичные теоремы 2.1 и следствие 2.2 утверждения можно доказать и когда правая часть системы (1) не обладает свойством T-периодичности по времени (т.е., когда неверны тождества (2)). В этом случае вместо оператора 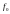, определяемого равенством (4), используется оператор

(10)

При этом предполагается, что среднее (10) существует, и предел (10), равномерен относительно из каждого фиксированного шара, а - равномерно непрерывен и ограничен на множестве (9).

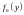Перейдем к задаче о T- периодических решениях системы (1) и к обсуждению возможностей приближенного построения этих решений при помощи системы (3). Предположим, что для некоторого ограниченного открытого множества векторное поле - не имеет нулевых точек на границе 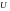. Тогда определен .

2.5. Теорема. Пусть .

Тогда существует такое , что при система (1) имеет по крайней мере одно T – периодическое решение , для которого справедливо соотношение . Причем для любой последовательности , сходящейся к нулю, последовательность решений 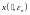вполне ограничена и ее предельными точками могут быть только состояния равновесия системы (3), лежащие в .

Важным случаем является ситуация, когда состояние равновесия системы (3) изолировано. Тогда определен индекс множества

нулевых точек векторного поля - в пространстве на шарах малых радиусов с центром в ., т.е. .

2.6. Следствие. Пусть .– изолированный нуль векторного поля , причем выполнено условие

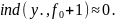
(11)

Тогда каждому r>0 соответствует такое >0, что при система (1) имеет по крайней мере одно Т- периодическое решение , для которого справедлива оценка

(12)

Через А обозначается следующая матрица

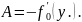
(13)

2.7. Следствие. Пусть .– нуль векторного поля , причём выполнено условие

(14)

Тогда каждому r>0 соответствует такое >0, что при система (1) имеет по крайней мере одно Т-периодическое решение , для которого справедлива оценка (12).