4.Відцентрові насоси

Принцип дії насоса

У відцентрових насосах всмоктування і нагнітання рідини проходить рівномірно і безперервно під дією відцентрової сили, що виникає при обертанні робочого колеса з лопатками, яке розміщене в спіралеподібному корпусі.

В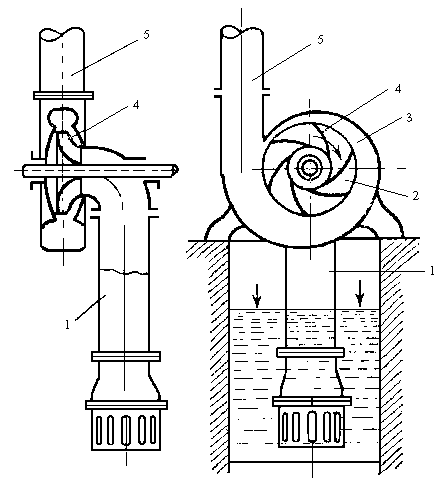 одноступінчатому відцентровому насосі рідина із всмоктуючого трубопроводу 1 поступає вздовж осі робочого колеса 2 в корпус 3 насосу і попадаючи на лопатки 4, набуває обертового руху. Відцентрова сила відкидає рідину в канал змінного перерізу між корпусом і робочим колесом, в якому швидкість рідини зменшується до значення рівного швидкості в нагнітальному трубопроводі 5.

Рис. Схема відцентрового насоса: 1- всмоктуючий трубопровід; 2- робоче колесо; 3- корпус; 4- лопатки; 5- нагнітальний трубопровід.

Я к випливає з рівняння Бернуллі, відбувається перетворення кінетичної енергії потоку рідини в статичний напір, що забезпечує підвищення тиску рідини. На вході в колесо створюється понижений тиск і рідина з ємності безперервно поступає в насос.

Рис. Схема багатоступінчатого насоса:

1- робоче колесо; 2- корпус; 3- вал; 4- відвідний канал.

Основне рівняння відцентрових машин Ейлера

В каналах між лопатками робочого колеса рідина, рухаючись вздовж лопаток, одночасно здійснює обертовий рух разом з колесом.

В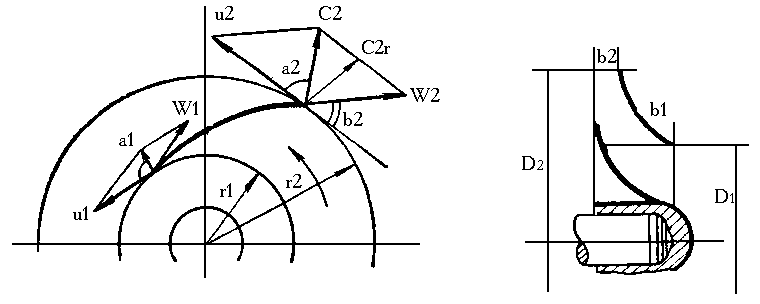 изначимо повний напір, що розвиває колесо при транспортуванні ідеальної рідини. Абсолютні швидкості руху рідин на вході в колесо С₁, на виході з колеса С₂ є кожна геометричною сумою відносної і колової швидкостей і їх можна розкласти на відносні складові ω₁ і ω₂ направлені вздовж лопаток, а також колові (направлені по дотичній до кола руху колеса) u₁ і u₂ .

Рис. До виведення основного рівняння відцентрових машин.

Приймемо за площину порівняння площину робочого колеса, складемо баланс енергії рідини при проходженні її через колесо за рівнянням Бернуллі (z₁ =z₂)

При обертанні колеса рідина на виході отримує додаткову енергію А на шляху довжиною r₂ - r₁.

Тоді

Якщо колесо рухається з кутовою швидкістю ω, то відцентрова сила С, яка діє на частину рідини масою m, рівна:

де r – біжучий радіус обертання частинки.

Робота А_G, яка здійснюється відцентровою силою при переміщенні цієї частини на шляху r₂ - r₁ складає:

Добуток ω·r=u.

Тоді А_G рівна:

Питома робота, віднесена до одиниці ваги рідини, рівна питомій енергії, яку отримує рідина в насосі:

Рівняння перепишеться у вигляді:

звідки:

Згідно рівняння Бернуллі, напори рідини на вході в колесо Н₁ і на виході з нього Н₂ складають:

Тоді теоретичний напір Н_т рівний:

Підставивши значення у рівняння отримуємо:

З паралелограмів швидкостей на вході в колесо і виході з нього

Тоді рівняння запишеться у вигляді:

(11)

Рівняння є основним рівнянням відцентрових машин і може бути використано для розрахунку всіх відцентрових машин (турбогазодувок, турбокомпресорів, вентиляторів та інш.).

Звичайно рідина, поступаючи із всмоктуючого трубопроводу, рухається по колу в радіальному напрямку. Кут між абсолютним значенням швидкості рідини на вході в робоче колесо і коловою швидкістю (умова без ударного поступлення рідини в колесо), тоді рівняння спрощується:

(12)

Дійсний напір насоса менше теоретичного, оскільки частина енергії рідини витрачається на подолання гідравлічних опорів всередині насоса і рідина в ньому при кінцевій кількості лопаток не рухається за подібними траєкторіями.

де - гідравлічний к.к.д. насоса, рівний 0.8-0.95; - коефіцієнт, який враховує кінцеву кількість лопаток в насосі, рівний 0.6-0.8.

Продуктивність відцентрового насоса рівна:

де - товщина лопаток; z – число лопаток; b₁ і b₂ – ширина робочого колеса на внутрішній і зовнішній поверхнях; С_1r і С_2r – радіальні складові абсолютних швидкостей на вході в колесо і виході з нього.

Закони пропорційності

Продуктивність і напір відцентрового насосу залежать від числа обертів робочого колеса. Продуктивність насосу прямо пропорційна радіальній складовій абсолютної швидкості на виході з колеса. Якщо змінити число обертів насосу від n₁ до n₂, то і продуктивність змінюється від Q₁ до Q₂, тобто:

(13)

Рис. Подібність паралелограмів швидкостей при зміні числа обертів колеса від n₁ до n₂.

Напір відцентрового насосу пропорційний квадрату колової швидкості, тобто: (14)

Потужність насосу пропорційна добутку продуктивності на його напір, звідки випливає, що:

(15)

Приведені рівняння носять назву законів пропорційності.

Характеристика насосу

Графічна залежність напору Н, потужності N_e і коефіцієнта корисної дії _н від його продуктивності Q при постійному числі обертів n називається характеристикою насосу. Ці характеристики отримують при випробуванні насосів.

Рис. Характеристика відцентрового насоса.

Із приведених графічних залежностей випливає, що із збільшенням продуктивності при n=const напір насосу зменшується, потужність зростає, а к.к.д. _н переходить через максимум.

У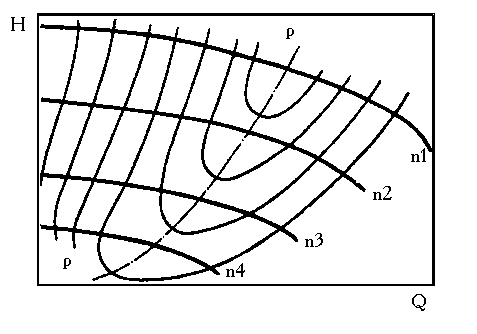 ніверсальна характеристика.

Рис. Універсальна характеристика відцентрового насосу.

Робота насосу на мережу

При виборі насосу необхідно враховувати характеристики насосу і мережі (система трубопроводів і апаратів, через які проходить рідина )

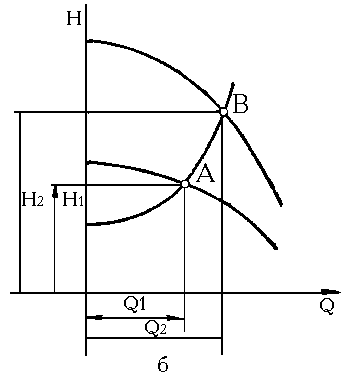
Рис. Суміщення характеристик насоса і мережі.

Відомо, що напір, який розвиває насос і враховуючи, що і відповідно

Одержимо (16)

Характеристика мережі виражається залежністю, яка являє собою рівняння параболи .

(17)

Точка Р – перетин двох кривих, називається робочою точкою і вона відповідає найбільшій продуктивності насосу Q₁ при його роботі на дану мережу.

Послідовне і паралельне з‘єднання насосів

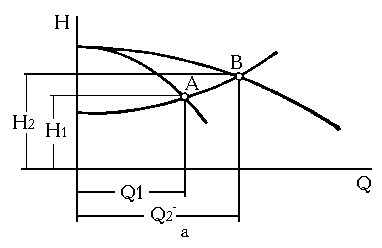
Рис. Сумісна робота насосів: а- паралельне з’єднання; б- послідовне з’єднання.

Часто виникає необхідність в роботі кількох насосів на одну мережу. Розрізняють паралельне і послідовне з‘єднання. При паралельному з‘єднанні двох насосів продуктивність зростає майже у два рази і дещо зростає напір, а при послідовному - навпаки.

Послідовне з’єднання двох насосів доцільно застосовувати при наявності крутих характеристик для збільшення напору ( приблизно збільшується в два рази).

Паралельне з’єднання двох насосів доцільно застосовувати при наявності похилих характеристик, коли продуктивність збільшується приблизно в два рази)