Исследование линейной зависимости

Одним из важнейших методов определения зависимости между X и Y является метод наименьших квадратов. Видя общее расположение точек, можно предположить, что эта зависимость линейная. Количество прямых, проходящих через заданную совокупность точек, бесконечно. Выберем оптимальную из них. Для этого суммарное отклонение между теоретическими и экспериментальными точками должно быть минимальным. Это отклонение мы найдем с помощью функции:

Метод нахождения минимального отклонения и есть метод наименьших квадратов. Это суммарное отклонение зависит от коэффициентов а и b функции Y, поэтому эти коэффициенты должны быть минимальными, то есть производная функции F(a, b) в этих точках равны нулю:

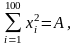
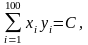
Пусть 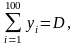N=100.

Получаем следующую систему:

Числа A, B, C и D считаем на компьютере. Используем данные расчетной таблицы и получаем систему уравнений с двумя неизвестными:

Далее, решая эту систему методом исключения переменных, получаем искомые числа a и b:

с ледовательно, уравнение прямой примет вид:

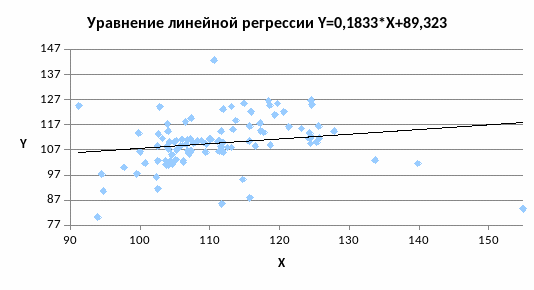
Аналогично ищем уравнение прямой вида:

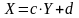
Для этого суммарное отклонение между теоретическими и экспериментальными точками должно быть минимальным. Это отклонение мы найдем с помощью функции:

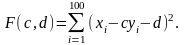
Суммарное отклонение зависит от коэффициентов c и d функции X, поэтому эти коэффициенты должны быть минимальными, то есть производная функции F(с, d) в этих точках равны нулю:

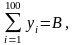
Пусть 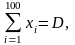N=100.

Получаем следующую систему:

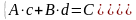
Числа A, B, C и D считаем на компьютере. Используем данные расчетной таблицы и получаем систему уравнений с двумя неизвестными:

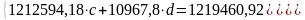
Далее, решая эту систему методом исключения переменных, получаем искомые числа c и d:

_{следовательно, уравнение прямой примет вид:}

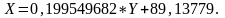
Исследование квадратичной зависимости

Линейные связи являются основными, но нередко встречаются и нелинейные связи, хорошо описываемые параболой, гиперболой и т. д.

В этой курсовой работе рассмотрим еще одну регрессию в форме параболы, которая также может описывать отклонения точек от кривой.

Уравнение регрессии в форме параболы второго порядка имеет вид: . Суммарное отклонение зависит от коэффициентов p, q и r этой функции. Как и в предыдущем исследовании, нам необходимо провести оптимальную кривую, т. е. найти минимум функции:

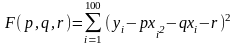
Известно, что минимум достигается в точках, где частные производные функции F(p, q, r) равны нулю. В нашем случае имеем:

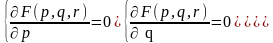
Продифференцировав данную функцию, получим следующую систему:

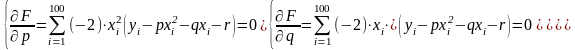
Введем следующие обозначения 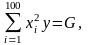N=100.

Получаем следующую систему:

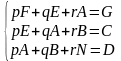
Числа A, B, C, D, E, F, G считаем на компьютере. При решении используем данные расчетной таблицы и получаем систему уравнений с тремя неизвестными:

Решаем данную систему методом Крамера, получаем искомые числа:

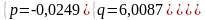
следовательно, искомое уравнение параболической регрессии имеет вид:

Y=-0,0249*X²+6,0087*X-248,22

Заключение

В данной работе при помощи статистических методов были прослежены закономерности и связи между двумя дискретными случайными величинами X и Y.

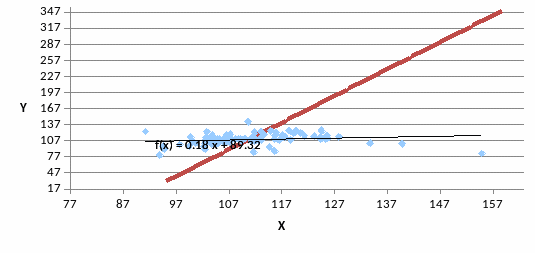
Для этих величин были посчитаны числовые характеристики дискретных случайных величин, построены гистограммы относительных нормированных частот, графики эмпирических функций распределения, графики полигонов относительных частот, приведены диаграммы рассеивания с линиями регрессии, а также корреляционная таблица для величин X и Y.

В результате было научно доказано, что зависимость между X и Y весьма слабая, но она существует. При возрастании X возрастает Y и наоборот.

Данные для обработки были взяты с сайта www.infostat.ru.