ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ МОСКОВСКОЙ ОБЛАСТИ

«Международный университет природы, общества и человека «Дубна»

Институт системного анализа и управления

Кафедра информатики и вычислительной техники

Кафедра высшей математики

КУРСОВАЯ РАБОТА

ПО

ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКЕ

ТЕМА: «Изучение характера зависимости между признаками X и Y»

Выполнил: студент 2013 группы 2 курса

Института системного анализа и управления

Ермолчев Алексей Юрьевич

Руководитель:

К.ф.-м.н., доцент Г. Э. Гришанина

Дата защиты:

Оценка:

Дубна, 2011

Содержание

Оглавление

Содержание 2

Введение 3

Основная часть 4

Выборочные числовые параметры 8

Расчёт коэффициента корреляции 9

Гистограммы относительных нормированных частот X и Y 11

Графики эмпирических функций распределения X и Y 12

Графики полигонов относительных частот X и Y 13

Регрессия 14

Метод наименьших квадратов 14

Заключение 19

Список литературы 21

Введение

Математическая статистика — наука о математических методах систематизации и использовании статистических данных для научных и практических выводов. Во многих своих разделах математическая статистика опирается на теорию вероятностей, позволяющую оценить надёжность и точность выводов, делаемых на основании ограниченного статистического материала (выборки).

Во время статистических наблюдений для каждого объекта в ряде случаев можно измерить значение нескольких признаков. Таким образом, получается многомерная выборка. Если многомерную выборку обработать по значениям отдельного признака, то получится обычная обработка одномерной выборки.

Смысл обработки многомерных выборок состоит в том, чтобы установить связь между признаками. Связи могу быть функциональными, то есть каждому значению одной величины соответствует определенное значение другой величины.

Если среднее значение одной случайной величины функционально зависит от значения другой случайной величины, то такая статистическая зависимость называется корреляционной.

Для обработки были выбраны индексы потребительских цен и тарифов на товары и услуги в Беларуси и России.

Основная часть

Для обработки были выбраны случайные величины X и Y. Случайная величина X – индексы потребительских цен и тарифов на товары и услуги в Беларуси. Случайная величина Y – индексы потребительских цен и тарифов на товары и услуги в России.

Даны выборки i=1,…, N, N=100.

X	Y	X	Y	X	Y	X	Y
109,4	106,1	97,7	100	115,7	116,4	124,5	126,8
104,5	105	102,3	96,2	106,5	118,2	124,3	113,6
107,3	106,6	139,8	101,6	107	105,4	113,1	124,2
103,6	102,8	154,9	83,6	106,2	102,1	118,4	126,5
105,1	103	105,5	107,7	117,2	117,6	114,9	125,4
103,8	108,3	116,5	108,5	124,2	111,6	118,6	124,7
102,5	108,5	115,7	87,9	111,9	109,9	113,3	115,1
105,8	108,6	94,7	90,6	111,3	106,5	111,6	114,4
106	111,1	114,7	95,2	109,1	109,9	109,5	109,2
111,3	110,6	118,7	108,9	100	106,2	115,6	110,5
111,1	110,3	111,9	106,1	99,8	113,6	120,6	122,1
112,5	107,9	103,2	111,5	94,5	97,3	91,2	124,5
113,1	107,9	110,1	111,3	133,7	102,9	124,5	112,2
93,9	80,2	107,7	109,7	107,3	119,6	125,3	110,1
106,2	102,7	111,6	108,4	117,3	114,6	125,7	111,7
103,8	102,3	102,6	113,3	111,9	123,2	127,8	114,4
103,7	101	105,2	107	119,3	120,9
102,5	102,7	106,8	111	102,8	124,1
104,2	102,4	105,2	110,7	124,6	124,9
104	101	108,2	110,5	121,3	116,2
111,7	85,5	104	114,4	110	111,3
110,6	142,7	104,9	110,1	104,2	110,1
108,8	110,7	123,1	115,5	124,4	109,5
102,5	91,5	113,7	118,7	117,7	113,9
104,4	102,4	104,1	107,1	103,9	117,4
104,6	101,3	107,2	111,4	125,6	116,5
100,7	101,7	106,6	109,2	115,9	122,2
99,5	97,5	106,8	106,6	119,7	125,4

На основании этой выборки строим диаграмму рассеивания и корреляционную таблицу X и Y:

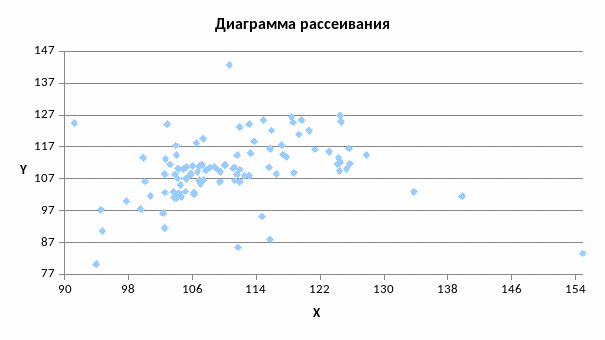
Корреляционная таблица:

X/Y	72,3875-80,2	80,2-88,0125	88,0125-95,825	95,825-103,6375	103,6375-111,45	111,45-119,2625	119,2625-127,075	127,075-134,8875	134,8875-142,7
83,2375-91,2	0	0	0	0	0	0	1	0	0
91,2-99,1625	1	0	1	2	0	0	0	0	0
99,1625-107,125	0	0	1	14	16	6	1	0	0
107,125-115,0875	0	1	1	0	18	3	4	0	1
115,0875-123,05	0	1	0	0	3	5	6	0	0
123,05-131,0125	0	0	0	0	2	7	2	0	0
131,0125-138,975	0	0	0	1	0	0	0	0	0
138,975-146,9375	0	0	0	1	0	0	0	0	0
146,9375-154,9	0	1	0	0	0	0	0	0	0

Приведем основные понятия и определения из курса теории вероятности и математической статистики, которые будут иметь место в данной работе.

Генеральная совокупность — совокупность объектов, из которых производится случайный выбор объектов для исследования.

Выборочная совокупность — отобранные случайным образом объекты из генеральной совокупности.

Объем генеральной (выборочной) совокупности — число объектов совокупности.

Варианта — наблюдаемое значение переменной.

Относительная частота — отношение числа наблюдений к объему выборки.

Диаграмма рассеивания (корреляционное поле) — график в ДПСК, на котором откладываются все пары точек .

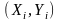Гистограмма относительных частот — ступенчатая фигура, состоящая из прямоугольников, основанием которых служит интервал длины 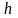, а высоты равны .

Выборочное среднее — среднее арифметическое значений вариант выборки .

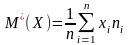Выборочная дисперсия — среднее арифметическое квадрата отклонения случайных величин от их среднего значения 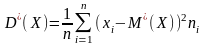. Исправленная дисперсия .

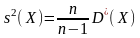Мода выборки — варианта с наибольшей частотой.

Ковариация (корреляционный момент) двух случайных величин 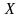и 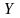— это математическое ожидание произведения отклонений случайных величин от их математического ожидания .

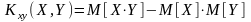Коэффициентом корреляции двух случайных величин заданных на одном вероятностном пространстве называется величина .

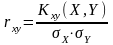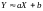
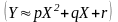Если для двух случайных величин и можно хотя бы приближенно записать, что , то говорят, что и связаны линейной (квадратичной) корреляцией.