6 Поверхности II порядка. Канонические уравнения

			Название поверхности	Каноническое уравнение
1	эллипсоид			(рис.1)
2	гиперболоиды	однополостный гиперболоид		(рис.2)
3		двуполостный гиперболоид		(рис.4)
4	конус			(рис.5)
5	пароболоиды		эллиптический параболоид	(рис.3)
6			гиперболический параболоид	(рис.6)
7	цилиндры		эллиптический цилиндр
8			гиперболический цилиндр
9			параболический цилиндр
10			пара плоскостей	левая часть уравнения распадается на произведение двух линейных множителей

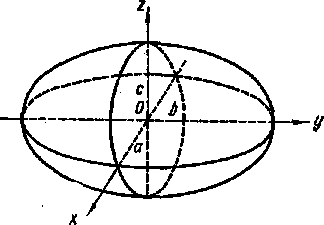
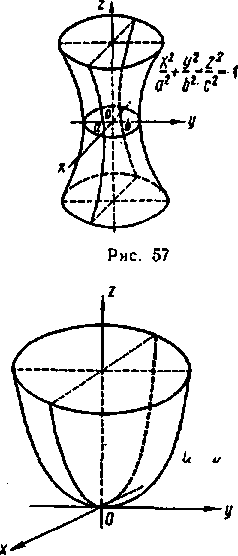
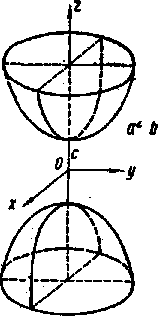Рисунок 1 Рисунок 2

Рисунок 3 Рисунок 4

Рисунок 5

Рисунок 6

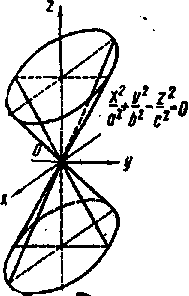
7 Варианты заданий

ЗАДАНИЕ 1

По координатам вершин треугольника АВС найти:1)длину стороны ВС;2)площадь треугольника АВС;3)уравнение ВС;4)уравнение высоты, проведенной из вершины А;5)длину высоты, проведенный из вершины А;6)расстояние от вершины А до стороны ВС;7)уравнение медианы, проведенной из вершины А до стороны ВС;8)уравнение биссектрисы внутреннего угла В; 9)угол В в радианах с точностью до 0,01.

1. А (4; 1), В (0;-2), С (-5; 10).

2. А (-7; 3), В (5;-2), С (8; 2).

3. А (5;-1), В (1;-4), С (-4; 8).

4. А (-14; 6), В (-2;1), С (1; 5).

5. А (6; 0), В (2;-3), С (-3; 9).

6. А (-9; 2), В (3;-3), С (6; 1).

7. А (7; -4), В (3:-7), С (-2;5).

8. А (-8; 4), В (4;-1), С (7; 3).

9. А (3; -3), В (-1;-6), С (-6; 6).

10. А (-6; 5), В (6;0), С (9; 4).

11. А (-6;-4), В (-10;-1), С (6; 1).

12. А (12; 0), В (18;8), С (0; 5).

13. А (-6;-2), В (-6;-3), С (10;-1).

14. А (8; 2), В (14;10), С (-4; 7).

15. А (2;-4), В (-2;-1), С (14; 1).

16. А (2;-1) В (8;7), С (-10; 4).

17. А (5;-3), В (1;10), С (17;2).

18. А (14;-6), В (20;2), С (2;-1).

19. А (3; 4), В (-1;7), С (15; 9).

20. А (1;-2), В (7;6), С (-11; 3).

21. А (-1; 1), В (7;5), С (4; 11).

22. А (-2; 1), В (6;7), С (3; 13).

23. А (2;-1), В (10;5), С (7; 11).

24. А (1; 1), В (9;7), С (6; 13).

25. А (-1; 2), В (7;8), С (4; 14).

ЗАДАНИЕ 2

1 Найти уравнение диагонали параллелограмма, не проходящей через точку пересечения его сторон Х+Y-1=0 и Y+1=0 , если известно, что диагонали параллелограмма пересекаются в точке (-1;0).

2 Найти координаты точки симметрично точке (2;-4) относительно прямой 4Х+ЗY+1=0.

3 Составить уравнение прямой, проходящей через точку А (-1:2) так, что середина ее отрезка, заключенного между параллельными прямыми Х+2Y+1=0 и Х+2Y-3=0, лежит на прямой Х-Y- 6=0.

4 Даны уравнения двух сторон треугольника 4Х-5Y+9=0 и Х+4Y-3=0. Найти уравнение третьей стороны, если известно, что медианы этого треугольника пересекаются в точке (3;1).

5 Вычислить координаты вершин ромба, если известны уравнения двух его сторон: 2Х-Y+4=0 и 2Х-Y+10=0, и уравнение одной из его диагоналей Х+Y+2=0.

6 Даны две вершины треугольника А (-4; 5) и В (4; 1) и точка пересечения его высот Д (3; 5). Составить уравнения сторон треугольника.

7 Даны уравнения высот треугольника АВС: ЗХ+2Y+6=0 и Х-Y+5=0 и координаты одной из вершин А (-5; 3). Найти уравнения сторон

треугольника.

8 Даны уравнения двух сторон треугольника: 5Х-2Y-8=0 и ЗХ-2Y-8=0. Составить уравнения третьей стороны треугольника, если известно, что ее середина совпадает с началом координат.

9 Составить уравнение сторон треугольника, зная одну из его вершин А(2;-3), и уравнения двух высот 7Х-2Y-10=0 и 2Х-7Y+3=0.

10 Даны уравнения основания равнобедренного треугольника Х+Y-4=0 и боковой стороны Х-2Y+4=0. Точка А (-2; 3) лежит на второй боковой стороне. Найти уравнение второй боковой стороны.

11 Даны две противоположные вершины ромба А (3; 4) и С (1;-2) и уравнение одной из его сторон Х-Y+1=0. Найти уравнения остальных

сторон ромба.

12 Даны середины сторон треугольника М (2; 1), N (5; 3), Р (3;-4). Составить уравнения сторон треугольника.

13 Составить уравнения сторон треугольника, если даны одна из его вершин (1; 3) и уравнения двух медиан: Х-2Y +1=0 и Y-1=0.

14 Составить уравнение прямой, проходящей через точку А (1; 3) так, что середина ее отрезка, заключенного между параллельными прямыми Х+2Y +5=0 и Х+2Y+1=0, лежит на прямой Х-Y-5=0.

15 Составить уравнение сторон треугольника, зная одну из его вершин А (0;2), и уравнения высот ВМ: Х+Y=4 и СМ: Y=2Х. М-точка пересечения его высот.

16 Стороны АВ и ВС параллелограмма АВСД заданы уравнениями 2Х-Y+5=0 и X-2Y+4=0, диагонали его пересекаются в точке М (1; 4). Найти длины его высот.

17 Найти вершины прямоугольного равнобедренного треугольника, если дана вершина прямого угла С (3;-1) и уравнение гипотенузы 3Х-Y+2=0.

18 Две стороны параллелограмма заданы уравнением Y=Х-2 и 5Y=Х+6. Диагонали его пересекаются в начале координат. Написать уравнение двух других сторон параллелограмма и его диагоналей.

19 Вычислить площадь ромба, зная одну из его вершин А (0; 1), точку

пересечения его диагоналей М (4; 4) и точку Р (2; 0) на стороне АВ.

20 Через точку пересечения прямых 2Х-5Y-1=0 и Х+4Y-7=0 провести

прямую, делящую отрезок между точками А (4;-3) и В (-1; 2) в отношении 2:3.

21 Определить, при каких значениях m и n прямая (2m-n+5)Х+7n+19=0 параллельна оси ОY, прямая и отсекает на оси ОХ отрезок, равный 5(считая от начала координат). Написать уравнение этой прямой.

22 Определить, при каком значении а прямая (а+2)х+(а²-9)у+3а² -8а+5=0:

1)параллельна оси абсцисс;

2)параллельна оси ординат;

3)проходит через начало координат.

В каждом случае написать уравнение прямой.

23 Две стороны квадрата лежат на прямых 5Х-12Y-65=0 и 5Х-12Y+26=0. Вычислить его площадь.

24 Даны две смежные вершины квадрата А (2; 0) и В (-1; 4). Составить уравнения его сторон и вычислить его площадь.

25 Точка А (5;-1) является вершиной квадрата, одна из сторон которого лежит на прямой 4Х-3Y-7=0. Составить уравнения прямых, на которых лежат остальные стороны этого квадрата.

ЗАДАНИЕ 3

Привести уравнение кривой второго порядка к каноническому виду и построить кривую.

1. а) 2х²-8х+у²-6у=0 б) х² +10х-4у+33=0

2. а) х² +4х-у²=0 б) у² -6х+2у-11=0

3. а) х²-8х-у²=0 б) х² -4х+5у+14=0

4. а) у²-6у-х²+2х=0 б) у² +х-4у+2=0

5. а) 6х² -25у² -18х-100у-316=0 б) х² -8х-3у+19=0

6. а) 5х² -6у²+10х-12у-31=0 б) у² -5х+6у+4=0

7. а) х² -4у²+6х+5=0 б) х² +6у+6х-6=0

8. а) 3х²-у² +12х-4у-4=0 б) у² +6х-8у+22=0

9. а) х² -4у²+2х-16у-7=0 б) х² +8х-2у+14=0

10. а) х² -4у²-4х+6у-5=0 б) у² -3х+10у+16=0

11. а) 4х²-9у² -8х+18у-23=0 б) 2х² -4х-у+3=0

12. а) 9х² -16у²-54х-64у-127=0 б) х-2у² +4у-3=0

13. а) х² +у²-2х+6у-5=0 б) х² -2х-у+2=0

14. а) х² +4у²+4х-8у-8=0 б) х-у² +2у-2=0

15. а) х² +2у²+8х-4=0 б) х² -2х+у+7=0

16. а) 4х² +9у²-40х+36у+100=0 б) х+у² -2у+3=0

17. а) 9х² -16у²-54х-64у-127=0 б) 2х² +8х+у+7=0

18. а) 9х² +4у²+18х-8у+49=0 б) х+2у² -4у+4=0

19. а) 4х² -у²+8х-2у+3=0 б) х² +4х+у+3=0

20. а) 2х² +3у²+8х-6у+11=0 б) х+2у² +4у+1=0

21. а) 3х² +3у²-6х+12у-5=0 б) х² +10х-4у+33=0

22. а) 3у² -х²+2х=2 б) у² -6х+2у-11=0

23. а) у² +4х²-2у=0 б) х² -4х+5у-6=0

24. а) 2х² +у²-6х=0 б) у² +3х+4у=0

25. а) 2х² -8х+у²+10у=3 б) х² -8х-3у+19=0

ЗАДАНИЕ 4

Построить график функции:

1.	14.
2.	15.
3.	16.
4.	17.
5.	18.
6.	19.
7.	20. .
8.	21.
9.	22.
10.	23. .
11.	24. .
12.	25. (ρ > 0).
13.

ЗАДАНИЕ 5

По координатам вершин пирамиды а₁ а₂ а₃ а₄ найти:

1) длины ребер а₁ а₂ и а₁ а₃ ;

2) угол между ребрами а₁ а₂ и а₁ а_з ;

3) площадь грани а₁ а₂ а₃ ;

4) объем пирамиды а₁ а₂ а₃ а₄ ;

5) уравнения прямых а₁ а₂ и а₁ а₃ ;

6) уравнения плоской а₁ а₂ а₃ и а₁ а₂ а₄ ;

7) угол между плоскостями а₁ а₂ а₃ и а₁ а₂ а₄ ;

8) угол между ребром а₁ а₃ и гранью а₁ а₂ а₄ ;

9) уравнение высоты, опущенной из вершины а₄ на грань а₁ а₂ а₃ ;

10) уравнение плоскости, проходящей через высоту пирамиды, опущенную из вершины а₄ на грань а₁ а₂ а₃ , и вершину а₁ пирамиды ;

11) расстояние от вершины. а₃ до плоскости а₁ а₂ а_4.

	а1	а2	а3	а4
1	(3;1;4)	(-1;6;1)	(-1;1;6)	(0;4;-1)
2	(3;3;9)	(6;9;1)	(1;7;3)	(8;5;8)
3	(3;5;4)	(5;8;3)	(1;9;9)	(6;4;8)
4	(2;4;3)	(7;6;3)	(4;9;3)	(3;6;7)
5	(9;5;5)	(-3;7;1)	(5;7;8)	(6;9;2)
6	(0;7;1)	(4;1;5)	(4;6;3)	(3;9;8)
7	(5;5;4)	(3;8;4)	(3;5;10)	(5;8;2)
8	(6;1;1)	(4;6;6)	(4;2;0)	(1;2;6)
9	(7;5;3)	(9;4;4)	(4;5;7)	(7;9;6)
10	(6;6;2)	(5;4;7)	(2;4;7)	(7;3;0)
11	(0;3;2)	(-1;3;6)	(-2;4;2)	(0;5;4)
12	(-1;2;0)	(-2;2;4)	(-3;3;0)	(-1;4;2)
13	(2;2;3)	(1;2;7)	(0;3;3)	(2;4;5)
14	(0;-1;2)	(-1;-1;6)	(-2;0;2)	(0;1;4)
15	(3;0;2)	(2;0;6)	(1;1;2)	(3;2;4)
16	(0;2;-1)	(-1;2;3)	(-2;3;-1)	(0;4;1)
17	(2;3;2)	(1;3;6)	(0;4;2)	(2;5;4)
18	(-1;0;2)	(-2;0;6)	(-3;1;2)	(-1;2;4)
19	(2;0;3)	(1;0;7)	(0;1;3)	(2;2;5)
20	(2;-1;2)	(1;-1;6)	(0;0;2)	(2;1;4)
21	(2;0;8)	(-10;3;0)	(-3;5;1)	(-1;-7;9)
22	(1;4;0)	(-5;1;-2)	(-3;1;-3)	(2;-7;9)
23	(3;7;9)	(-3;0;7)	(2;-3;-5)	(1;-2;0)
24	(-1;3;5}	(5;-1;-3)	(-2;9;-2)	(8;0;1)
25	(5;1;-7)	(2;-3;-1)	(-7;-1;1)	(3;4;-5)

ЗАДАНИЕ 6

Составить общее уравнение плоскости, проходящей через точку М перпендикулярно плоскостям  и :

	M		
1	(2;1;-5)	3X-2Y+Z+7=0	5X-4Y+3Z+1=0
2	(1;-1;1)	X-Y+Z-1=0	2X+Y+Z+1=0
3	(2;-1;1)	3X+2Y-Z+4=0	X+Y+Z-3=0
4	(1;8;2)	5X+6Y+11Z-3=0	3X+Y+4Z-12=0
5	(-1;-2;0)	4X+6Y-5Z-14=0	X+3Y-2Z-1 =0
6	(5;1;2)	X-7Y-2Z-10=0	2X-2Y-Z-13=0
7	(2;4;1)	X-2Y+5Z-7=0	2X-3Y+7Z-5=0
8	(1;1;1)	X-2Y+2Z+8=0	3X+5Y+7Z-1=0
9	(1;4;5)	X+Y+5Z+3=0	3X+2Y+8Z-9=0
10	(3;0;7)	X+Y+4Z=0	3X+2Y+7Z-2=0

Составить уравнение плоскости, проходящей через точки М₁, М₂ перпендикулярно плоскости  :

	М1	М2	
11	(2;-1;4)	(3;2;1)	X+Y+Z-3=0
12	(1;1;1)	(2;2;2)	X-Y-Z=0
13	(0;-5;0)	(0;0;2)	X+5Y+2Z-10=0
14	(2;0;-1)	(1;-1;3)	3X+2Y-Z+3=0
15	(-1;-2;0)	(1;1;2)	X+2Y+2Z-4=0
16	(1;-2;4)	(2;-3;5)	X+Y-3Z+8=0
17	(0;1;3)	(1;2;7)	X+2Y+5Z+6=0
18	(1;1;0)	(2;-1;-1)	5X+2Y+3Z-7=0
19	(1;4;0)	(2;14;3)	X+6Y+Z-3=0
20	(9;1;1)	(19;2;2)	17X+2Y+Z+11=0
21	(7;1;0)	(26;2;3)	9X+Y+Z-17=0
22	(0;1;2)	(-1;2;3)	X+Y-Z+2=0
23	(3;4;6)	(5;1;5)	X+2Y+3Z-6=0
24	(4;1;0)	(2;-1;1)	X-Y+Z-3=0
25	(1;0;1)	(-1;1;0)	X+2Y-Z-1=0

ЗАДАНИЕ 7

Составить канонические уравнения прямой, заданной как линия пересечения двух плоскостей  и :

		
1	x-2у+2z-8=0	x+2z-6=0
2	3x-5y+z-8=0	2x+y-z+2=0
3	x-2y+3z-4=0	3x+2y-5z-4=0
4	x+z-6=0	x+6y-4=0
5	x+2y-4=0	x-2y+2z-8=0
6	x+2Z-6=0	x+y+z-6=0
7	x+2y+3z-13=0	3x+y+4z-14=0
8	x+2y+3z-1=0	2x-3y+2z-9=0
9	2x+7y-z-8=0	Х+2y+z-4=0

Составить канонические уравнения прямой, проходящей через точку А параллельно прямой ℓ:

	А	ℓ
10	(3;1;-1)	X+5y+2=0 3х+4y+2z-8=0
11	(2;0;-3)
12	(-4;3;0)	x-2y+z-4=0 2x+y-z=0
13	(2;-5;9)	2x-3y-3z-9=0 x-2y+3=0

Составить канонические уравнения прямой, проходящей через точку А перпендикулярно прямым ℓ₁ и ℓ₂:

	А	ℓ1	ℓ2
14	(2;-3;4)
15	(0;1;1)
16	(2;-3;4)	x=t;y=t;z=2t+5	x=3t+8;y=2t-4;z=t+2
17	(0;1;-1)	x=3t+1;y=15t;z=7t-2	x=t;y=2t-5;z=6
18	(0;-1;1)	x=2t;y=t-5;z=3t-2	x=4t-1;y=4t+6;z=t-4

Составить канонические уравнения прямой, проходящей через точки а₁ и а₂ :

	а1	а2
19	(1;-2;1)	(3;1;1)
20	(1;-2;1)	(0;6;5)
21	(3;1;2)	(0;2;5)
22	(0;1;2)	(5;2;1)
23	(1;7;3)	(0;2;1)
24	(1;0;2)	(5;1;4)
25	(3;5;1)	(2;3;1)

ЗАДАНИЕ 8

Найти проекцию точки А на плоскости :

	А	
1	(1;3;1)	x+2y+2z-30=0
2	(3;1;-1)	3x+y+z-20=0
3	(5;2;-1)	2x-y+3z+23=0
4	(4;-3;1)	x-2y-z-15=0
5	(1;-1;0)	5x-6y+2z-76=0

Найти точку, симметричную точке А относительно плоскости а:

	А	а
6	(0;0;0;)	х-2у+4z-21=0
7	(1;5;2)	2х-у-z+11=0
8	(1;-3;-4)	Зх-у-2z=0
9	(5;2;-1)	2х-у+3z+23=0
10	(3;-4;-6)	9х-7у-31z-108=0

Найти точку, симметричную точке А относительно прямой ℓ :

	А	ℓ
11	(2;1;0)
12	(4;3;10)
13	(1;-1;2)
14	(3;2;0)
15	(2;-1;5)
16	(0;0;0;)

Составить уравнения прямой, проходящей через точки пересечения плоскости а с прямыми ℓ₁ и ℓ₂:

	А	ℓ1	ℓ2
17	2x+y-3z=0
18	3x-2y+z=0
19	6x+3y-41=0
20	3x-y-2z+5=0
21	2x+3y+z-1=0

Составить уравнения прямой, лежащей в плоскости  и проходящей через точку пересечения плоскости  с прямой ℓ, перпендикулярно вектору а :

		ℓ	_ а
22	6x+3y-z-41=0		{1;2;1}
23	x+2y=0		{3;-1;2}
24	x+2y=0		{5;-1;2}
25	3x-y-2z+5=0		{0;3;5}

ЗАДАНИЕ 9

Составить общее уравнение плоскости, проходящей через параллельные прямые ℓ₁ и ℓ₂:

	ℓ1	ℓ2
1
2
3	x=2t+1;y=-t;z=t+1
4
5

Составить общее уравнение плоскости, проходящей через прямую ℓ₁, параллельно прямой ℓ₂ :

	ℓ1	ℓ2
6
7
8
9
10	x=3t-1;y=-2t-3;z=-t+2	x=2t+2;y=3t-1;z=-5t+1

Составить общее уравнение плоскости, проходящей через точку М параллельно прямым ℓ₁ и ℓ₂:

	ℓ1	ℓ2	М
11			(-2;0;0)
12			(6;1;1)
13			(1;2;1)
14			(1;2;3)
15			(0;0;2)

Составить общее уравнение плоскости, проходящей через пересекающиеся прямые ℓ₁ и ℓ₂:

	ℓ1	ℓ2
16
17	x=z-2;y=2z+1
18		x=t+5;y=-4t-1;z=t-4
19	x=t+1;y=-2;z=-t+1	x=2t;y=2t-2;z=-3t+2
20		x=3t+7;y=2t+2;z=-2t+1
21
22	x=2t-3;y=3t-2;z=-4t+6	x=t+5;y=-4t-1;z=t-4
23
24	x=2t+1;y=3t-2;z=-6t+1
25

ЗАДАНИЕ 10

Установить вид поверхности и построить её эскиз:

	а)	б)
1	x2 + y2 =z2	y=6 z2
2		x= 2z2
3	z= x2 + y2
4
5	x2 +y2+z2-6x+8y+10z+25=0	z=1- x2 - y2
6		z+(x2 + y2)=0
7		4x2 -12y2-6z=12
8	2x2 -5y2-8=0	4x2 -8y2+16z2=0
9	3x2 +5y2 =12z
10	x2 + 4y2 -8=0
11	z2 -4x=0	2x2 -y2-z2=0
12	8x- y2-2z2 =0	y2 =6x-4
13	4z= x2 -y2	x2 +y2 = 2(z-1)2
14	8x2 -4y2+24z2-48=0	x2 + y2=2z
15	2y2+z2=1-x	2x2 +3z2=12y
16	3x2 -y2-z2=3
17	z2 +4z-2x+6=0	3x2 -y2-z2=3
18		2x2 -4y2+8z2=0
19	x=9y2	x2 -2y2+z2=1
20	z2 +2z-4x+1=0	2x2 +8y2-16=0
21
22	2x2 +z2=1-y	y2=-6z
23		x2 -2z2+4y2=0
24		x2+2y2=4z
25	4x2-y2-2z2=0

в)x²+y²+z²+2а₁x+2b₁y+2с₁z+g₁=0

1		2		3
4		5		6
7		8		9
10		11		12
13		14		15
16		17		18
19		20		21
22		23		24
25

Список литературы

1. Бортаковский А. С. Аналитическая геометрия в примерах и задачах: учеб.пособие для втузов/А.С.Бортаковский, В.Пантелеев. -М :Высш.шк.,2005.-496с.

2. Бортаковский А. С. Линейная алгебра в примерах и задачах: учеб пособие для втузов/А.С.Бортаковский, А.В.Пантелеев.-М.:Высш.шк., 2005.-591с.

3. Выгодский М.Я. Справочник по высшей математике.-М.:Астрель, ACT,2002.-992с.

4. Высшая математика для экономистов: учеб.для вузов/под ред.Н. Ш. Кремера.-2-е изд.,перераб.и доп.-М.:ЮНИТИ,2002.-471с.

5. Канатников А.Н. Аналитическая геометрия: учеб.для втузов/А.Н. Канатников, А.П.Крищенко; под ред. В.С.Зарубина, А.П.Крищенко.-4-е изд.,испр.-М.:Изд-во МГТУ им. Н.Э.Баумана,2005.-392с.

6. Письменный Д. Т. Конспект лекций по высшей математике Изд.-М.:Айрис-пресс, 2004. Ч.1.-288с.

7. Привалов И.И. Аналитическая геометрия: учебник.-32-е изд.-СПб :Лань,2003.-304с.