§ 2.8 Поляризованность. Напряженность поля в диэлектрике

Обычно в отсутствие внешнего электрического поля дипольные моменты молекул диэлектрика или равны нулю (неполярные молекулы), или ориентированы беспорядочным образом (полярные молекулы). В обоих случаях суммарный дипольный момент диэлектрика равен нулю.

Под действием внешнего поля диэлектрик поляризуется, т.е. приобретает отличный от нуля дипольный момент = , где  дипольный момент одной молекулы. Для количественного описания степени поляризации диэлектрика пользуются векторной величиной  поляризованностью, определяемой как дипольный момент единицы объема диэлектрика:

= = , (8.1)

и характеризующей поляризацию в данной точке. Поэтому поляризованность может служить характеристикой, как для неоднородного внешнего поля, так и для неоднородного диэлектрика.

В изотропных диэлектриках при не очень больших значениях Е поляризованность связана с напряженностью поля соотношением

=æ₀ , (8.2)

где æ – не зависящая от напряженности величина, называемая диэлектрической восприимчивостью диэлектрика.

Диэлектрическая восприимчивость æ - величина безразмерная, причем всегда æ > 0, и для большинства диэлектриков (твердых и жидких) составляет несколько единиц (хотя, например, для спирта æ  25, для воды æ = 80).

Для установления количественных закономерностей поля в диэлектрике внесем в однородное внешнее электростатическое поле с напряженностью (создается двумя бесконечными параллельными разноименно заряженными плоскостями) пластинку из однородного изотропного диэлектрика, расположив ее так, как показано на рисунке 14. Под действием поля диэлектрик поляризуется, т. е. происходит смещение зарядов: положительные смещаются по полю, отрицательные  против поля. В результате этого на правой грани диэлектрика, обращенного к отрицательной плоскости, будет избыток положительного заряда с поверхностной плотностью +, на левой  отрицательного заряда с поверхностной плотностью . Эти не скомпенсированные заряды, появляющиеся в результате поляризации диэлектрика, называются связанными. Так как их п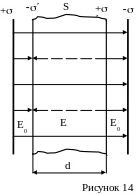 оверхностная плотность  меньше плотности  свободных зарядов плоскостей, то не всё поле компенсируется полем зарядов диэлектрика (число силовых линий, проходящих через единицу площади в диэлектрике и вне его различно в связи с тем, что часть линий напряженности пройдет сквозь диэлектрик, другая же часть  обрывается на связанных зарядах). Следовательно, поляризация диэлектрика вызывает уменьшение в нем поля по сравнению с первоначальным внешним полем. Вне диэлектрика напряженность поля равна . Таким образом, появление связанных зарядов приводит к возникновению дополнительного электрического поля (поля, создаваемого связанными зарядами), которое направлено против внешнего поля (поля, создаваемого свободными зарядами) и ослабляет его. Результирующая напряженность поля внутри диэлектрика равна

Е = Е₀  Е. (8.3)

Напряженность поля, созданного двумя бесконечными заряженными плоскостями согласно (6.5) Е=/₀, поэтому

Е = Е₀  . (8.4)

Определим поверхностную плотность связанных зарядов . Полный дипольный момент пластинки диэлектрика p_v = PV = PSd, где S  площадь грани пластинки, d  ее толщина. С другой стороны, полный дипольный момент, согласно (5.2), равен произведению связанных зарядов каждой грани q=S на расстояние d между ними, т.е. p_v = Sd. Таким образом, PSd = Sd, откуда следует, что

 = Р, (8.5)

т. е. поверхностная плотность связанных зарядов  равна поляризованности Р.

Подставив в (8.4) выражения (8.5) и (8.2), получим

Е = Е₀  æЕ,

откуда напряженность результирующего поля внутри однородного диэлектрика равна

Е = Е₀/(1+æ) = Е₀/ . (8.6)

Безразмерная величина

 = 1 + æ (8.7)

называется диэлектрической проницаемостью среды. Диэлектрическая проницаемость среды  показывает, во сколько раз поле ослабляется диэлектриком, характеризуя количественно свойство диэлектрика поляризоваться в электрическом поле. Соотношение (8.6) в векторной форме:

= /. (8.8)

Так как напряженность электрического поля в диэлектрике уменьшается в  раз, то следует ожидать, что все рассмотренные ранее для вакуума физические величины (например, кулоновская сила, напряженность поля точечного заряда, потенциал точечного заряда, потенциальная энергия взаимодействия точечных зарядов) также уменьшатся в  раз. Соответственно соотношения для названных величин (2.1), (3.3), (4.9) и (4.7) в сплошном, однородном, изотропном диэлектрике с диэлектрической проницаемостью  примут вид:

F=k ; Е= ;  = ; W= . (8.9)