§ 8.41 Ток смещения

Согласно Максвеллу, если всякое переменное магнитное поле возбуждает в окружающем пространстве вихревое электрическое поле, то должно существовать и обратное явление: переменное электрическое поле должно вызывать появление в окружающем пространстве вихревого магнитного поля (второе основное положение теории Максвелла). Так как магнитное поле есть основной обязательный признак всякого тока, то Максвелл назвал переменное электрическое поле током смещения, в отличие от тока проводимости, обусловленного движением заряженных частиц (электронов и ионов).

Понятие тока смещения можно пояснить при помощи следующего опыта. Представим себе цепь переменного тока, содержащую конденсатор. Для суждения о наличии тока в контуре включим последовательно с конденсатором небольшую лампочку накаливания, играющую роль демонстрационного амперметра. Если бы контур был подключен к источнику постоянного тока, то через такой разомкнутый конденсатором контур постоянный ток не проходит и при длительном включении источника лампочка не обнаруживает никакого накала (лампочка кратковременно будет вспыхивать только в момент подключения источника). При подключении контура в осветительную цепь переменного тока (частотой 50 Гц) перезарядки конденсатора будут следовать непрерывно друг за другом с частотой 100 раз в секунду, и в контуре длительно будет существовать переменный ток. В этом случае отдельные вспышки лампочки уже не будут заметны, и лампочка будет накаливаться равномерно.

Можно отметить, что, в отличие от постоянного тока, переменные токи могут существовать и в разомкнутых контурах. При этом всякий раз, когда в разомкнутом контуре имеется ток, между его концами (между обкладками конденсатора) имеется изменяющееся во времени электрическое поле или ток смещения. Таким образом, токи проводимости в металлическом проводнике замыкаются токами смещения в диэлектрике.

Согласно Максвеллу электрическое поле в конденсаторе в любой момент времени создает такое же магнитное поле, как если бы между обкладками существовал ток проводимости с силой, равной силе тока в металлических проводах. Или, иными словами, магнитное поле нашего разомкнутого контура оказывается таким же, как если бы контур был замкнут.

Это позволяет найти количественную связь между изменяющимся электрическим полем и вызываемым им магнитным полем. Напряженность поля между обкладками плоского конденсатора согласно (6.5) равна E₀ = /₀, но если пространство между обкладками заполнено диэлектриком с проницаемостью , то напряженность в соответствии с (8.6) будет в  раз меньше, т.е.

Е = /₀. (41.1)

Согласно (9.1) электрическое смещение D и напряженность поля Е связаны соотношением

D = ₀Е, (41.2)

где под  подразумевается модуль поверхностной плотности заряда.

Сравнивая выражения (41.1) и (41.2), находим, что электрическое смещение D в конденсаторе равно поверхностной плотности заряда  на обкладках:

D = . (41.3)

Поэтому полный заряд q на каждой из обкладок равен:

q = S = SD,

где S – площадь обкладок.

Если за время dt заряд конденсатора изменяется на dq, то сила тока в проводе равна

I = = S .

Она однозначно связана с быстротой изменения электрического смещения (индукции электрического поля). Отсюда следует, что меняющееся поле конденсатора вызывает такое же магнитное поле, как ток, имеющий силу SdD/dt или плотность тока

. (41.4)

Эта величина получила название плотности тока смещения.

Пользуясь этим понятием, можно второе положение Максвелла сформулировать в следующем виде: переменное во времени электрическое поле вызывает такое же магнитное поле, как и ток проводимости с плотностью , определяемый формулой (41.4).

В общем случае электрическое поле может быть неоднородным и может зависеть не только от времени, но и от координат. В этом случае выражение для плотности тока смещения будет

= , (41.5)

где знак частной производной указывает на то, что магнитное поле зависит от быстроты изменения индукции электрического поля во времени в каждой точке поля.

Следует подчеркнуть, что ток смещения определяется производной вектора , но не самим этим вектором.

Подчеркнем, что термин «ток смещения» является чисто условным. По существу ток смещения – это изменяющееся со временем электрическое поле. Основанием для того, чтобы назвать «плотностью тока» величину (41.5), служит лишь то, что размерность этой величины совпадает с размерностью плотности тока. Из всех физических свойств, присущих действительному току, ток смещения обладает лишь одним – способностью создавать магнитное поле.

Если в каком-либо проводнике имеется переменный ток, то внутри проводника существует переменное электрическое поле. Поэтому внутри проводника имеются и ток проводимости, и ток смещения, и магнитное поле проводника определяется их суммой, т.е. полным током. Плотность полного тока

= + . (41.6)

В зависимости от электропроводности среды и быстроты изменения поля (частоты переменного тока) оба слагаемых в (41.6) играют разную роль. В хорошо проводящих веществах (металлах) и при низких частотах плотность тока смещения мала, и током смещения можно пренебречь по сравнению с током проводимости. Напротив, в плохо проводящих средах (изоляторах) и при высоких частотах ток смещения играет основную роль.

Оба члена в формуле (41.6) могут иметь и одинаковые знаки и противоположные. Поэтому полный ток может быть как больше, так и меньше тока проводимости и в частном случае может обращаться в нуль.

Такой пример приведен на рисунке 53, где изображен сферический конденсатор, заполненный проводящей средой. Если заряд обкладок есть q, то электрическое смещение D на расстоянии R от центра равна

D = q/4R².

Плотность тока смещения равна

J_см = ,

а сила тока смещения равна

I_см = 4R²J_см = .

При разряде конденсатора этот ток направлен от внутренней обкладки к наружной. Ток же проводимости направлен противоположно (от плюса к минусу) и его сила есть

I =  .

Поэтому полный ток

I_полн = I + I_см = 0

и, несмотря на движение зарядов между обкладками, магнитное поле равно нулю.

Т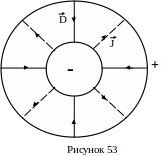 аким образом, в общем случае меняющихся токов магнитное поле определяется не током проводимости, а полным током. Если мы имеем разомкнутый контур, то на концах проводника обрывается лишь ток проводимости. В диэлектрике же между концами проводника имеется ток смещения, который замыкает ток проводимости. Поэтому, если под электрическим током понимать полный ток, определяемый формулой (41.6), то окажется, что в природе все электрические токи замкнуты. Этот важный вывод также был получен Максвеллом.

Максвелл обобщил теорему о циркуляции вектора (см. (36.9)), введя в ее правую часть полный ток I_полн = сквозь поверхность S, натянутую на замкнутый контур L. Тогда обобщенная теорема о циркуляции вектора запишется в виде

= I_полн = . (41.7)

Выражение (41.7) справедливо всегда, свидетельством чего является полное соответствие теории и опыта.