§ 4.19 Разветвленные цепи. Правила Кирхгофа

Расчет разветвленных цепей, например, нахождение сил токов в отдельных ее ветвях, значительно упрощается при применении правил Кирхгофа, чем при применении обобщенного закона Ома для всех ее отдельных ветвей (Г. Р. Кирхгоф (18241887)  немецкий физик). Этих правил два. Первое из них относится к узлам цепи. Любая точка разветвления цепи, в которой сходится не менее трех проводников с током, называется узлом. При этом ток, входящий в узел, считается имеющим один знак (например, плюс), а ток, выходящий из узла,  имеющим другой знак (например, минус).

Первое правило Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю

= 0. (19.1)

Например, применительно к рисунку 24 первое правило Кирхгофа запишется так:

I₁ + I₂  I₃ = 0.

П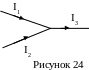 ервое правило Кирхгофа вытекает из закона сохранения электрического заряда. Действительно, в случае установившегося постоянного тока ни в одной точке проводника и ни на одном его участке не должны накапливаться электрические заряды. В противном случае вместе с зарядами менялось бы во времени и электрическое поле, а потому токи не могли бы оставаться постоянными.

Второе правило Кирхгофа: для любого замкнутого контура разветвленной цепи алгебраическая сумма произведений сил токов в отдельных участках этого контура на сопротивления соответствующих участков равна алгебраической сумме ЭДС в этом контуре

= . (19.2)

К аждое из произведений IR в (19.2) определяет разность потенциалов, которая существовала бы между концами соответствующего участка, если бы ЭДС в нем была равна нулю, т.е. это произведение есть падение напряжения, вызываемого протекающим по R током. Поэтому второе правило Кирхгофа можно выразить следующим образом: для любого замкнутого контура алгебраическая сумма всех падений напряжения равна алгебраической сумме всех ЭДС в этом контуре.

Рассмотрим контур, состоящий из трех участков (рисунок 25). Направление обхода по часовой стрелке примем за положительное, отметив, что выбор этого направления совершенно произволен. Все токи, совпадающие по направлению с направлением обхода контура, считаются положительными, не совпадающие с направлением обхода  отрицательными. Источники ЭДС считаются положительными, если они создают ток, направленный в сторону обхода контура. Затем применим к каждому из трех участков обобщенный закон Ома (см. (18.5)):

I₁ R₁ = ₂  ₃  E₁,

I₂ R₂ = ₃  ₁  E₂,

I₃ R₃ = ₁  ₂ + E₃.

Сложив эти равенства, приходим после сокращения всех потенциалов к формуле (19.2), т.е. ко второму правилу Кирхгофа. Таким образом, уравнение (19.2) является следствием закона Ома для неоднородных участков цепи.

При расчете разветвленных цепей постоянного тока с применением правил Кирхгофа необходимо:

- выбрать произвольное направление токов на всех участках цепи; действительное направление токов определяется при решении задачи  если искомый ток получится положительным, то его направление было выбрано правильно, отрицательным  его истинное направление противоположно выбранному;

- выбрать направление обхода контура и строго его придерживаться; произведение IR положительно, если направление тока на данном участке совпадает с направлением обхода, и наоборот. ЭДС, действующие по выбранному направлению обхода, считаются положительными, против  отрицательными;

- составить столько уравнений, чтобы их число было равно числу искомых величин (в систему уравнений должны входить все сопротивления и ЭДС рассматриваемой цепи). При этом надо следить, чтобы одни уравнения не являлись следствием других;

- если в разветвленной цепи N узлов, то независимые уравнения типа (19.1) можно составить лишь для N-1 узлов, так как уравнение для последнего узла будет следствием предыдущих. Если в разветвленной цепи можно выделить несколько замкнутых контуров, то независимые уравнения типа (19.2) можно составить только для тех контуров, которые не получаются в результате наложения уже рассмотренных.