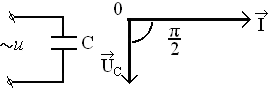- •Лабораторна робота №1
- •Електрична схема до лабораторної роботи
- •Результати вимірів та розрахунків
- •Вимірювання основних параметрів електричного кола: напруги та сили струму. Розширення меж вимірювання приладів
- •Програма підготовки до виконання завдання
- •Особливості правил техніки безпеки
- •Методичні рекомендації до виконання завдання
- •Теоретичні відомості
- •Цифрові вимірювальні прилади
- •Вимірювання потужності та енергії в електричних колах змінного струму.
- •Особливості правил техніки безпеки
- •Методичні рекомендації до виконання завдання
- •Теоретичні відомості
- •Вимірювання опорів
- •Програма підготовки до виконання завдання
- •Особливості правил техніки безпеки
- •Методичні рекомендаціі до виконання завдання
- •Теоретичні відомості
- •Дослідження характеристик електричних джерел освітлення
- •Програма підготовки до виконання завдання
- •Особливості правил техніки безпеки
- •Методичні рекомендації щодо виконання завдання
- •Теоретичні відомості
- •Аналіз та розрахунок нерозгалуженого кола однофазного струму
- •Програма підготовки до виконання завдання
- •Особливості правил техніки безпеки
- •Методичні рекомендації щодо виконання завдання
- •Теоретичні відомості
- •Дослідження трифазного електричного кола змінного струму при з’єднанні споживачів «зіркою» і «трикутником»
- •Програма підготовки до виконання завдання
- •Особливості правил техніки безспеки
- •Методичні рекомендації до виконання завдання
- •Теоретичні відомості.
- •Дослідження лінійного електричного кола постійного струму
- •Робоче завдання
- •Програма підготовки до виконання завдання
- •Особливості правил техніки безпеки
- •Методичні рекомендації щодо виконання завдання
- •Додаткове завдання
- •Теоретичні відомості
- •Контрольні запитання
- •Дослідження роботи однофазного силового трансформатора
- •Методичні рекомендації до виконання завдання
- •Теоретичні відомості
- •Дослідження трифазного асинхронного двигуна
- •Програма підготовки до виконання завдання
- •Особливості правил техніки безпеки
- •Методичні рекомендації до виконання завдання
- •Теоретичні відомості
- •Пуск та реверсування асинхронних електродвигунів
- •Методичні рекомендації до виконання завдання
- •Теоретичні відомості
- •Дослідження роботи двигуна постійного струму з послідовним та паралельним збудженням.
- •Робоче завдання
- •Програма підготовки до виконання завдання
- •Методичні рекомендації щодо виконання завдання
- •Додаткове завдання
- •Теоретичні відомості
- •Втрати та ккд машин постійного струму
- •Дослідження універсального двигуна
- •Робоче завдання
- •Програма підготовки
- •Методичні рекомендації до виконання завдання
- •Теоретичні відомості
- •Контрольні запитання
- •Дослідження параметрів змінного струму
- •Робоче завдання
- •Програма підготовки
- •Методичні рекомендації до виконання завдання
- •Теоретичні відомості до лабораторної роботи.
- •Дослідження параметрів електричного кола при паралельному з’єднанні двох або більше генераторів змінного струму.
- •Програма підготовки
- •Методичні рекомендації до виконання завдання
- •Теоретичні відомості
- •Дослідження лінійного електричного кола постійного струму
- •Робоче завдання
- •Програма підготовки до виконання завдання
- •Методичні рекомендації до виконання завдання
- •Теоретичні відомості
- •Контрольні запитання
- •Дослідження трифазного електричного кола змінного струму при з’єднанні споживачів зіркою та трикутником
- •Програма підготовки до виконання завдання
- •Методичні рекомендації до виконання завдання
- •Теоретичні відомості
- •Дослідження напівпровідникових випрямлячів.
- •Програма підготовки
- •Методичні рекомендації до виконання завдання
- •Теоретичні відомості
- •Основна література
- •Додаткова література
Теоретичні відомості
Параметри електричного кола змінного струму
На практиці частіше використовують енергію змінного струму ніж постійного. Переваги використання змінного струму у порівнянні з постійним полягають насамперед у тому, що електроенергію можна передавати на далекі відстані при значно вищій напрузі, а це економічно вигідно. Тобто змінний струм можна трансформувати. Електродвигуни та генератори змінного струму компактніші і мають кращий ККД.
Змінним називають такий струм, величина та напрям протікання якого змінюються з часом. Змінний струм, який використовується в промисловості, побуті і т. д. є такий, що змінюється в часі за синусоїдним законом і виробляється генераторами змінного струму. Його будову у спрощеній формі зображено на рис. 3. Основні складові спрощеної моделі генератора: постійний магніт, обертова рамка f1,f2; контактні кільця К1,k1,k2,К2 і щітки Щ1,Щ2. У рамці, що обертається в магнітному полі, за законом електромагнітної індукції (закон М. Фарадея – 1831р.) створюється змінна ЕРС індукції.
При
різних положеннях рамки відповідні
миттєві значення ЕРС будуть виражені
формулою:
 ,
де:
–
індукція магнітного поля;
,
де:
–
індукція магнітного поля;
 – ЕРС
у рамці;
– ЕРС
у рамці;
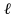 –
довжина
активної частини рамки;
–
довжина
активної частини рамки;
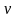 –швидкість
активної частини рамки;
–швидкість
активної частини рамки;
α – кут між напрямком векторами швидкості та магнітної індукції.
Якщо
α = 0 то і е
= 0;
при α = 90% миттєве значення ЕРС
=
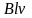 =
=
 .
Звідки
.
Звідки
 (1)
(1)

а
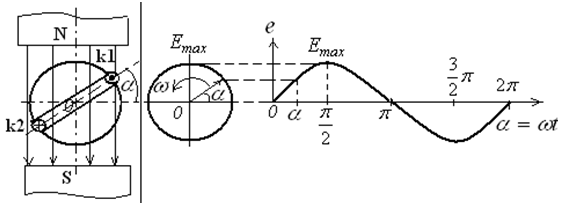
б в
Рис. 3. Схема генератора змінного струму та графічне зображення
характеру ЕРС і струму, що виникають у рамці.
Отже, при обертанні рамки, при її вертикальному розташуванні буде індукуватися найбільше значення ЕРС, а при горизонтальному положенні ЕРС дорівнюватиме нулю. Напрям індукованого струму можна визначити за правилом правої руки.
Для
більшої наочності й полегшення розрахунків
змінного значення ЕРС – е
скористаємось методом векторних діаграм.
Зобразимо амплітудне значення
електрорушійної сили
 одиничним обертовим радіус-вектором
(рис.3, в), який обертається синхронно з
рамкою. Очевидно миттєве значення ЕРС
в рамці дорівнює проекції радіус-вектора
на вісь ординат і визначається кутом
повороту рамки
одиничним обертовим радіус-вектором
(рис.3, в), який обертається синхронно з
рамкою. Очевидно миттєве значення ЕРС
в рамці дорівнює проекції радіус-вектора
на вісь ординат і визначається кутом
повороту рамки
 .
Сила струму на активному навантаженні
змінюється аналогічно. Тому миттєві
значення ЕРС, сили струму та напруги,
залежно від кута повороту рамки, можна
вирахувати так:
.
Сила струму на активному навантаженні
змінюється аналогічно. Тому миттєві
значення ЕРС, сили струму та напруги,
залежно від кута повороту рамки, можна
вирахувати так:
;
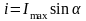 ;
;
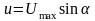 (2)
(2)
Відомо,
що певне положення коливної системи у
даний момент називається фазою. У нашому
випадку фаза визначається величиною
кута
,
на який повернулась рамка в магнітному
полі і вимірюється в кутових одиницях
або радіанах. Якщо рамка за час t
повернеться
на кут
,
то кутова швидкість її руху
 (3).
(3).
За
один період Т рамка повернеться на кут
 -
радіан. Тоді
-
радіан. Тоді
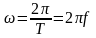 .
.
Де:
 –
частота обертання рамки.
–
частота обертання рамки.
- кутова швидкість обертання рамки або циклічна частота струму (ЕРС ) у рамці.
Підставивши вирази 1 і 2 у вираз 3 отримаємо миттєві значення ЕРС та струму:
 ;
;
 ;
;
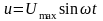 .
.
Якщо
в період часу
 рамка знаходилась під деяким кутом
до горизонтального положення, то такий
стан буде називатися початковою фазою.
Тому в загальному вигляді останні вирази
набудуть такого вигляду:
рамка знаходилась під деяким кутом
до горизонтального положення, то такий
стан буде називатися початковою фазою.
Тому в загальному вигляді останні вирази
набудуть такого вигляду:
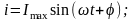


Отже,
кожна електрична величина, яка змінюється
за законом синуса, характеризується
амплітудою
 ,
фазою ωt ±
φ,
початковою фазою φ, циклічною частотою
.
,
фазою ωt ±
φ,
початковою фазою φ, циклічною частотою
.
Якщо
два значення Е.Р.С. або інші параметри
однакової частоти з однаковими фазами
коливання і будь-якими амплітудними
значеннями
 змінюються
за законами синусів, то кажуть що Е.Р.С.
збігаються за фазою.
змінюються
за законами синусів, то кажуть що Е.Р.С.
збігаються за фазою.
Якщо Е.Р.С. досягатимуть своїх максимальних або нульових значень неодночасно, тоді кажуть, що Е.Р.С. зсунуті за фазою одна відносно одної (рис. 4 - а,б).
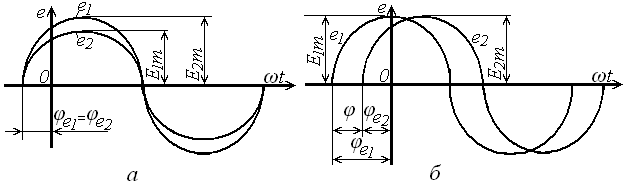
Рис. 4. Графіки зміни ЕРС (струму) від часу:
а – з однаковими фазами коливань; б – зсунуті по фазі.
Виникає
питання, як саме буде змінюватись
потужність змінного струму та як
визначити енергію в колі змінного
струму. Для постійного струму закон
Джоуля-Ленца можна записати в такому
вигляді
 .
Де:
.
Де:
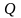 -
кількість виділеної теплоти у провіднику;
-
кількість виділеної теплоти у провіднику;
- омічний опір провідника;
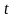 -
час протікання стуму;
-
час протікання стуму;
- сила струму.
У
випадку протікання змінного струму,
кількість виділеної енергії
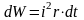 .
У даний вираз підставимо формулу 2:
.
У даний вираз підставимо формулу 2:
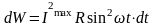 .
.
Сумарне
значення енергії, що виділиться у
провіднику за період
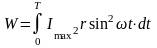 ;
;
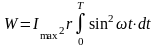 .φ
.φ
З
тригонометрії відомо, що
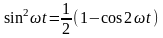 .
Отже,
.
Отже,
 ).
Звідки
).
Звідки
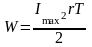 ,
так як другий інтеграл дорівнює нулю.
Перепишемо останній вираз у такій формі:
,
так як другий інтеграл дорівнює нулю.
Перепишемо останній вираз у такій формі:
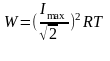
Введемо
позначення
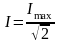 ,
тоді
,
тоді
 .
(4)
.
(4)
Де: - діюче значення струму.
Діючим
(ефективним) значенням змінного струму
називають таке значення постійного
струму, при якому на однаковому активному
опорі кола за той самий час виділиться
така сама кількість енергії, що й при
змінному. Діючі значення сили струму,
напруги та Е.Р.С. позначають прописними
латинськими літерами без індексів -
І,
U,
Е,
а їх числове значення можна записати
так:
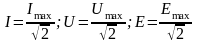 .
Зауважимо, що електровимірювальні
прилади градуюють у діючих значеннях
згаданих величин.
.
Зауважимо, що електровимірювальні
прилади градуюють у діючих значеннях
згаданих величин.
Активно-реактивні навантаження у колах змінного струму
Як відзначалося вище, електричні кола змінного струму значно відрізняються від характерних електричних кіл постійного струму. Для кола з джерелом живлення постійної напруги навантаженням є лише так званий омічний опір R, тоді як у колах змінного струму навантаженням може бути активний r, індуктивний - XL, ємнісний - XC та повний - Z опори.
Розглянемо вплив активного, індуктивного та ємнісного опорів на параметри та характеристики електричних кіл.
Активний опір у колі змінного струму
Опір провідника, як відомо з фізики, залежить від його довжини, площі поперечного перерізу та питомого опору :
 ,
де :
,
де :
– питомий опір;
– довжина провідника;
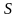 –
площа
поперечного перерізу.
–
площа
поперечного перерізу.
Відзначимо, що один і той же провідник у колах постійного та змінного струму має різну величину. Це пов’язано з явищем поверхневих струмів (скін-ефектом).
Навколо провідника, у якому протікає змінний струм створюється змінне магнітне поле. На рухомі заряди це поле буде діяти з силою, напрям якої визначається за правилом лівої руки. Очевидно, рухомі заряди будуть виштовхуватись на поверхню провідника. Разом з тим, густина вектора магнітної індукції тим більша, чим ближче до осі провідника, а тому електричний стум розподіляється переважно по поверхні провідника. Особливо це стосується високочастотних струмів.
Можна уявити, що струм у даному випадку протікає не по всій площі перерізу провідника, а по «трубі». При збільшенні частоти струму, стінка «провідної труби» зменшується, а тому опір провідника збільшується.
Звичайно, у колах постійного струму густина струму на всьому поперечному перерізі провідника однакова.

Рис. 5. Активне навантаження в колі змінного струму:
а – електрична схема;
б – графік залежності сили струму та напруги від часу;
в – векторна діаграма.
Якщо
до електричного кола з активним опором
(рис. 5), підвести змінну напругу
,
то по ньому протікатиме струм
 ,
де
,
де
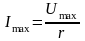 .
Поділивши
обидві частини останнього
рівняння
на
.
Поділивши
обидві частини останнього
рівняння
на
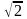 отримаємо
закон Ома для діючих значень струму та
напруги
отримаємо
закон Ома для діючих значень струму та
напруги

Отже в колі змінного струму з активним опором закон Ома справедливий для миттєвих, амплітудних і діючих значень.
Причому, на активному опорі струм та напруга збігаються за фазою.
Миттєве
значення потужності

Підставивши
вирази миттєвих значень струму та
напруги, отримаємо рівняння для миттєвого
значення потужності:
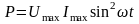 .
.
Оскільки
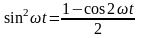 ,
то вираз для потужності запишеться
через діючі значення струму інапруги
таким чином:
,
то вираз для потужності запишеться
через діючі значення струму інапруги
таким чином:
 (5).
(5).
На
рис. 6 зображено графік залежності
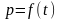 .
З виразу (5) та графіку (рис. 6) слідує, що
потужність буде пульсуючою і завжди
матиме додатне значення.
.
З виразу (5) та графіку (рис. 6) слідує, що
потужність буде пульсуючою і завжди
матиме додатне значення.

Рис. 6. Графік потужності при активному навантаженні
в колі змінного струму.
Середнє
значення діючої потужності за період
дорівнює:
 ;
;
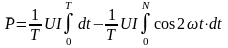 .
.
Оскільки
другий інтеграл дорівнює нулю, то середнє
значення потужності на активному опорі
дорівнює добутку діючих значень струму
та напруги
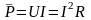
Активна потужність вимірюється у Вт, кВт, мВт.
Активна енергія, що виділяється на активному споживачі
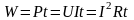 .
Вона вимірюється у
ватсекундах
(Втс), кіловатгодинах (кВт.год).
.
Вона вимірюється у
ватсекундах
(Втс), кіловатгодинах (кВт.год).
Активна електрична енергія необоротно перетворюється в інші види енергії: механічну – у двигунах, теплову – в електронагрівних приладах, у променеву і теплову в освітлювальних лампах тощо.
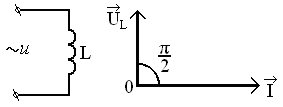
Індуктивний опір у колі змінного струму
Нехай до котушки індуктивності підведена змінна напруга (рис. 7). У результаті протікання змінного струму в котушці (без осердя) навколо неї виникає змінне магнітне поле, а в котушці наводиться ЕРС самоіндукції . Де: L – індуктивність котушки; - швидкість зміни струму в котушці.
При
відсутності активного опору
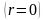 підведена напруга, відповідно другому
закону Кірхгофа, зрівноважується цією
ЕРС. Тобто
підведена напруга, відповідно другому
закону Кірхгофа, зрівноважується цією
ЕРС. Тобто
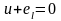 ;
;
 .
.
Перепишемо
останній вираз
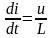 .
Оскільки миттєве значення напруги
.
Оскільки миттєве значення напруги
,
то
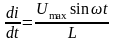 ;
;
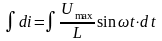 ;
;
 .
(6)
.
(6)
Отже,
у колах змінного струму з індуктивним
навантаженням струм відстає від напруги
на
 або
або
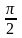 .
Позначимо добуток
.
Позначимо добуток
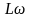 через індуктивний опір
та перепишемо вираз 6:
через індуктивний опір
та перепишемо вираз 6:
 (7)
(7)
Підставивши вираз 6 у вираз 7, отримаємо закон Ома для амплітудних значень сили струму і напруги:
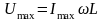 ,
,
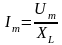 .
(8)
.
(8)
Аналітичне значення параметрів кола зобразимо за допомогою векторної діаграми (рис. 7,б):
|
Рис. 7. Індуктивне навантаження в колі змінного струму: а – електрична схема; б – векторна діаграма. |
Поділивши
обидві частини рівняння 8 на
, отримаємо закон Ома для діючих значень
струму та напруги
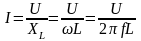 .
Де
.
Де
 - індуктивний опір.
- індуктивний опір.
Миттєва активна потужність на індуктивному навантаженні дорівнює добутку миттєвих значень сили струму та напруги:
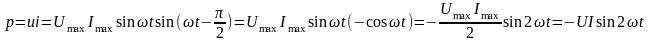 З
останнього виразу бачимо, що реактивна
потужність пульсує у колі з подвійною
частотою. Визначимо її середнє значення
за період:
З
останнього виразу бачимо, що реактивна
потужність пульсує у колі з подвійною
частотою. Визначимо її середнє значення
за період:
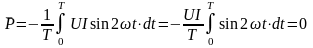
Отже, реактивна потужність буде циркулювати між індуктивним навантаженням та джерелом струму з подвійною частотою, але активна складова потужності за період дорівнює нулю.
Ємність у колах змінного струму
Нехай електричне коло складається лише з конденсатора, що не має активного опору, до якого підведено змінну напругу (рис. 8).
|
Рис. 8. Ємнісне навантаження в колі змінного струму: а – електрична схема; б – векторна діаграма. |
З
фізики відомо, що ємність провідника
(конденсатора)
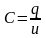 , де
, де
 -
заряд конденсатора,
-
заряд конденсатора,
 -
миттєве значення напруги.
-
миттєве значення напруги.
Нехай підведена напруга змінюється за законом .
Миттєве
значення сили струму в електричному
колі
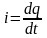 .
Або з врахуванням попереднього виразу:
.
Або з врахуванням попереднього виразу:
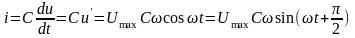 .
.
Очевидно струм досягне свого амплітудного значення при . Тобто
 при
при
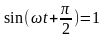 .
(9)
.
(9)
Позначивши
 та поділивши обидві частини рівняння
9 на
,
отримаємо
закон Ома для діючих значень струму та
напруги
та поділивши обидві частини рівняння
9 на
,
отримаємо
закон Ома для діючих значень струму та
напруги
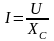 .
Миттєве значення активної складової
потужності
.
Миттєве значення активної складової
потужності
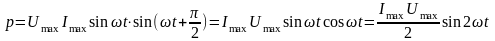 .
.
Через
діючі значення цей вираз запишеться
так:
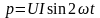 .
.
Середнє значення активної складової потужності за період
 .
.
З останнього виразу бачимо, що реактивна енергія в колі з змінюється навантаженням циркулює з подвійною частотою. Причому, у першу чверть періоду конденсатор заряджається, а в другу розряджається, при цьому міняється знак потужності, а енергія віддається назад в коло і т.д. Проте активна потужність, як і у випадку з індуктивним навантаженням, дорівнює нулю.
Коефіцієнт потужності
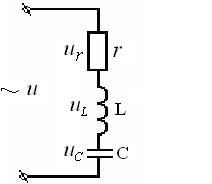
Розглянемо електричне коло в якому послідовно з’єднані ємнісне, індуктивне та активне навантаження (рис. 9). Очевидно сила струму у всіх видах навантажень однакова, т.я. вони з’єднані послідовно.
|
Рис. 9. Послідовне зєднання активного r, індуктивного L та ємнісного C навантажень. |
Миттєві значення струмів та напруг у колі запишуться так:
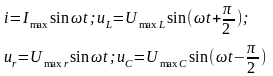
Запишемо
2 закон Кірхгофа для миттєвих та діючих
значень напруг на окремих дільницях
даного кола: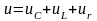 ,
, (1)
(1)
Побудуємо
векторну діаграму для спадів напруг у
колі (рис. 10). За основу беремо діюче
значення струму. На активному навантаженні
напруга і сила струму (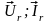 )
співпадають за фазою. Їх вектори
напрямлені уздовж горизонтальної лінії.
)
співпадають за фазою. Їх вектори
напрямлені уздовж горизонтальної лінії.
Вектори
спадів напруг на ємнісному та індуктивному
навантаженнях
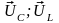 відповідно відстають та випереджають
за фазою струм
відповідно відстають та випереджають
за фазою струм
 на
кут
.
Тому їх вектори розташовані уздовж
вертикальної лінії і мають протилежні
напрямки.
на
кут
.
Тому їх вектори розташовані уздовж
вертикальної лінії і мають протилежні
напрямки.
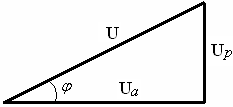
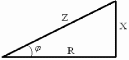
З наведених діграм отримуємо так званий трикутник напруг (рис. 11), за яким можна вирахувати сумарну напругу U.
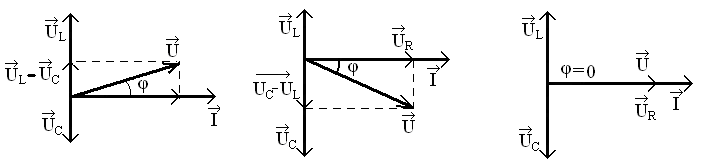
UL>UC UC>UL UC=UL
Рис. 10. Векторні діаграми для послідовного з’єднання активного, індуктивного та ємнісного навантажень, при різному
співвідношенні спадів напруг на них.
Поділивши
діючі значення напруг у рівнянні 1 на
діюче значення сили струму
,
отримаємо вираз для активного, індуктивного
та ємнісного опорів. Повний опір кола
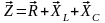 .
На основі цього виразу побудуємо векторну
діаграму, отримаємо так званий «трикутник
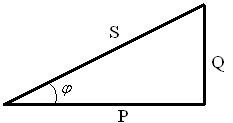
опорів» (рис. 12). З трикутника визначимо
повний опір кола
.
На основі цього виразу побудуємо векторну
діаграму, отримаємо так званий «трикутник
опорів» (рис. 12). З трикутника визначимо
повний опір кола
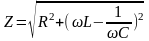 (10).
(10).
|
|
Рис. 11.Трикутник напруг |
Рис. 12. Трикутник опорів. |
Закон Ома для такого кола запишеться так:
 (11)
(11)
З виразу 11 бачимо, що при рівності індуктивного та ємнісного опорів діюче значення сили струму в колі буде найбільшою. Тобто, активна складова сили струму найбільша при компенсації ємнісного та індуктивного опорів, а таке явище називають резонансом струмів.
Якщо
ж помножити на діюче значення сили
струму
ліву та праву частини рівняння 1, то ми
отримаємо вираз для потужностей у колі
змінного струму з активним, ємнісним
та індуктивним опорами:
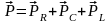 .
.
На цій основі можна побудувати трикутник потужностей (рис. 13).
З векторної діаграми видно, що споживана активна потужність такого електричного кола .
Позначимо
суму ємнісної та індуктивної складових
потужностей літерою
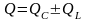 ,
тоді повна або, так звана, позірна
потужність,
,
тоді повна або, так звана, позірна
потужність,
 .
(12)
.
(12)
Величину
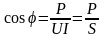 називають коефіцієнтом потужності.
Коефіцієнт потужності показує долю
активного навантаження Р
від загальної споживаної потужності
S.
називають коефіцієнтом потужності.
Коефіцієнт потужності показує долю
активного навантаження Р
від загальної споживаної потужності
S.
|
Рис. 13. Трикутник потужностей |
Аналізуючи
векторну діаграму та вираз 12, можна
зробити висновок, що в електричних колах
змінного струму циркулює тим більша
потужність, чим більший реактивний опір
при однаковій активній складовій
потужності
 .
Це явище негативно позначається на
роботі електромережі, так як в обмотках
генераторів, трансформаторів та
споживачів циркулюють високі струми,
які не використовуються споживачами.
Тому для раціонального використання
електромережі потрібно домагатися
балансу між ємнісним та індуктивним
навантаженнями. З цією метою на
підприємствах, де переважає індуктивне
навантаження, ставлять спеціальні
компенсатори або блоки ємностей, що дає
можливість досягти резонансу струмів
або до цього явища наблизитись, щоб
коефіцієнт потужності
.
Це явище негативно позначається на
роботі електромережі, так як в обмотках
генераторів, трансформаторів та
споживачів циркулюють високі струми,
які не використовуються споживачами.
Тому для раціонального використання
електромережі потрібно домагатися
балансу між ємнісним та індуктивним
навантаженнями. З цією метою на
підприємствах, де переважає індуктивне
навантаження, ставлять спеціальні
компенсатори або блоки ємностей, що дає
можливість досягти резонансу струмів
або до цього явища наблизитись, щоб
коефіцієнт потужності
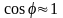 .
.
Контрольні запитання
1. Пояснити зміст та послідовність виконання лабораторної роботи?
2. Якими параметрами характеризують однофазний змінний струм?
3. Якими способами можна виразити змінний струм, напругу, е.р.с.?
4. Яке співвідношення фаз коливання струму і напруги в колах з активним, індуктивним та ємнісним навантаженням? Виразити алгебраїчно та векторно.
5. Що називають діючим значенням сили струму, напруги, е.р.с., та як їх вирахувати?
6. Зобразити графічно залежність i=f(t) для активного, індуктивного та ємнісного навантаження.
7. побудувати векторну діаграму для кола з трьома видами навантажень – активним, індуктивним та ємнісним.
8. Побудувати трикутник напруг, опорів та потужностей.
9. Що таке резонанс напруг?
10. Що називають коефіцієнтом потужності?
Лабораторна робота № 6