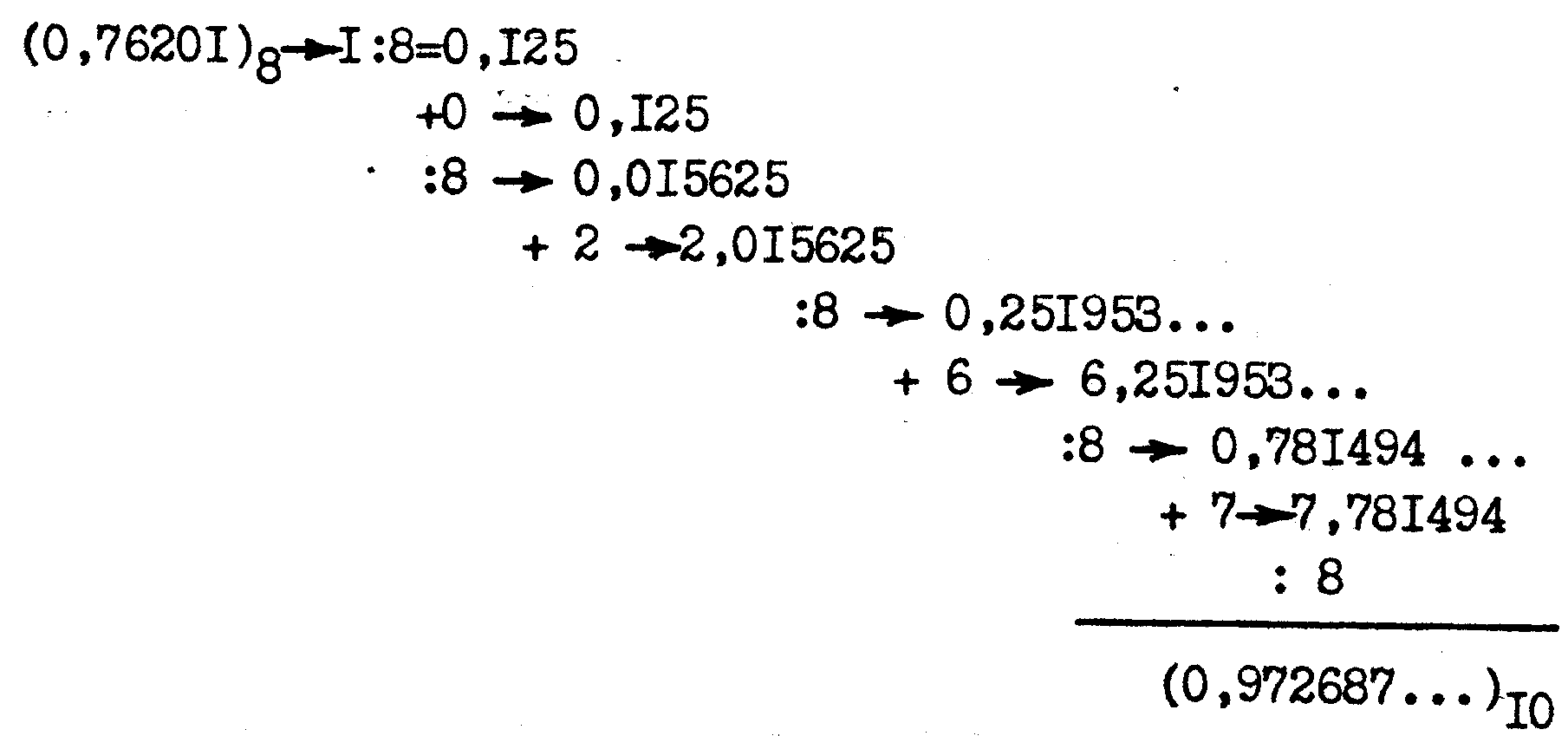Алгоритм перевода дробных чисел из системы счисления с основанием q2 в десятичную систему.

Дробное число, представленное по схеме Горнера может иметь следующий вид:

A(q₂)=((…(b_-s:q₂+b_-(s-1)):q₂+…+b_-2):q₂+b_-1):q₂

Отсюда - аналогично предыдущему - алгоритм перевода выглядит следующим образом:

1. Разделить младшую цифру числа (b_-s) на основание систе­мы счисления (q₂) (или умножить на 1/q₂ ).

2. Добавить к предыдущему результату следующую по порядку цифру числа.

3. Разделить предыдущий результат на основание системы счисления (или умножить на обратную величину).

4. Повторять п.2 и п.3 до тех пор, пока при выполнении п.2 не окажется добавленной старшая цифра числа; после этого один раз выполнить п.3

Все операции выполняются в десятичной системе счисления.

Пример: Перевести восьмеричное число 0,76201 в десятичное.

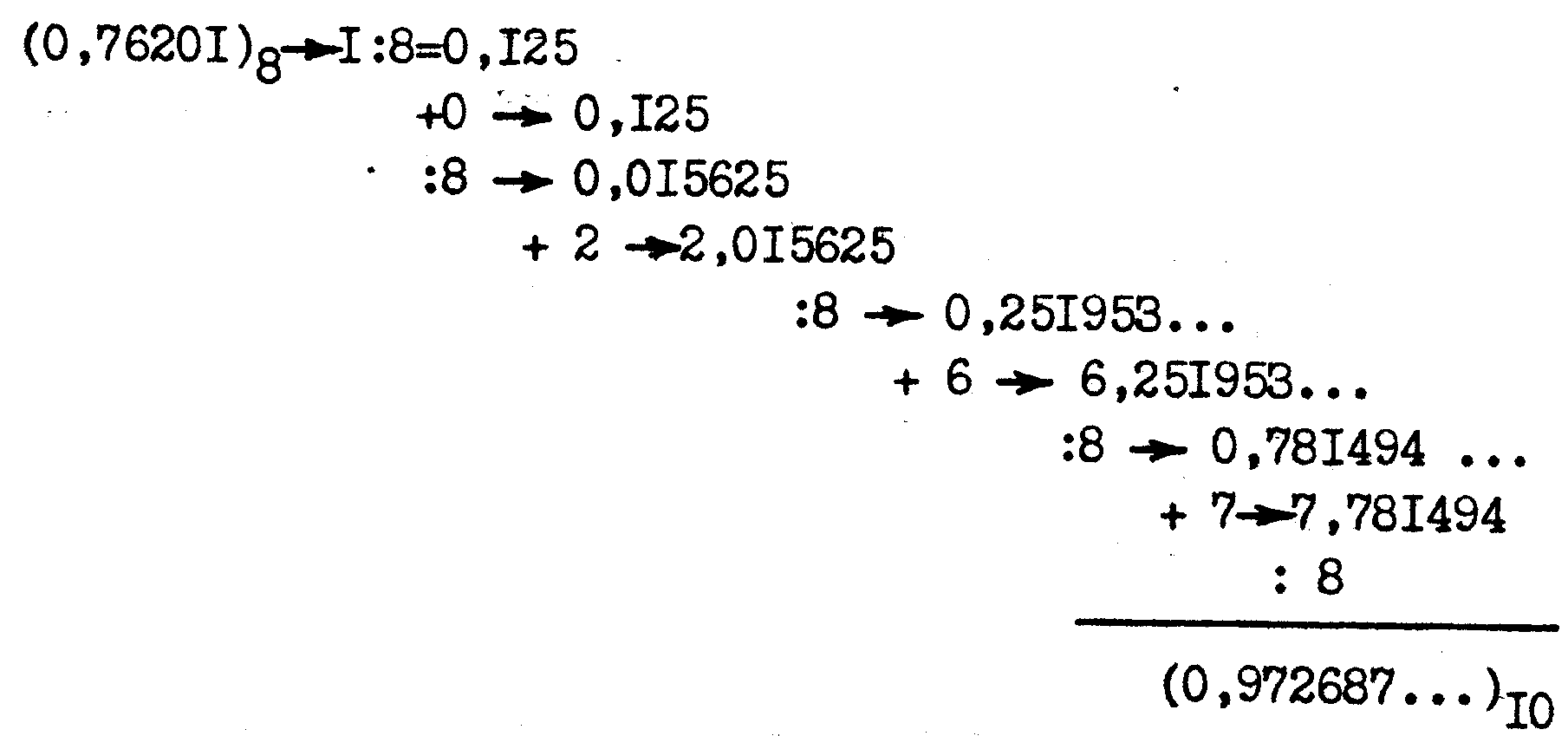
Использование промежуточной системы счисления

Этот метод применяют при переводе из десятичной системы счисления в двоичную и наоборот. В качестве промежуточной системы счисления чаще всего используют системы по основанию 2^k.

A=121₁₀?₈?₂