Перевод целых чисел

Целое число A (q₁) в системе с основанием q₂ может быть записано в следующем виде:

A(q₂)=b_k-1^. q₂^k-1+b_k-2^. q₂^k-2+…+b₁^. q₂¹+b₀^. q₂⁰

Выражение по схеме Горнера будет иметь вид:

A(q₂)=(…(( b_k-1^. q₂ + b_k-2)q₂ + b_k-3)q₂ + … +b₁) q₂ + b₀ (1.6)

Согласно правилу правую часть выражения разделим на величину основания q₂. В результате определим первый остаток b₀ и целую часть

z₁ = (…(( b_k-1^. q₂ + b_k-2)q₂ + … + b₁). Разделив целую часть на q₂ найдем второй остаток b₁ и целую часть z₂. Повторяя процесс деления к-1 раз, получим последнее целое частное b_k-1, которое, по условию, меньше основания системы q₂ и является старшей цифрой числа, представленного в системе с основанием q₂.

Пример: Перевести десятичное число А=98 в двоичную систему счисления (q₂ =2) .

Решение:

Ответ : A₍₂₎=1100010₍₂₎

Алгоритм перевода целых чисел из сс с q1 в десятичную

1. Умножить старшую цифру числа (аn) на основание системы счисления (q);

2. Добавить к предыдущему результату следующую по порядку цифру числа.

3. Умножить результат предыдущей операции на q.

4. Повторять п. 2 и 3 до тех пор, пока при выполнении п.2 не будет добавлена младшая цифра числа; на этом дейст­вии прервать операции.

Все операции выполняются при этом в десятичной системе.

Пример: Перевод восьмеричного числа 76201 в десятичную систему.

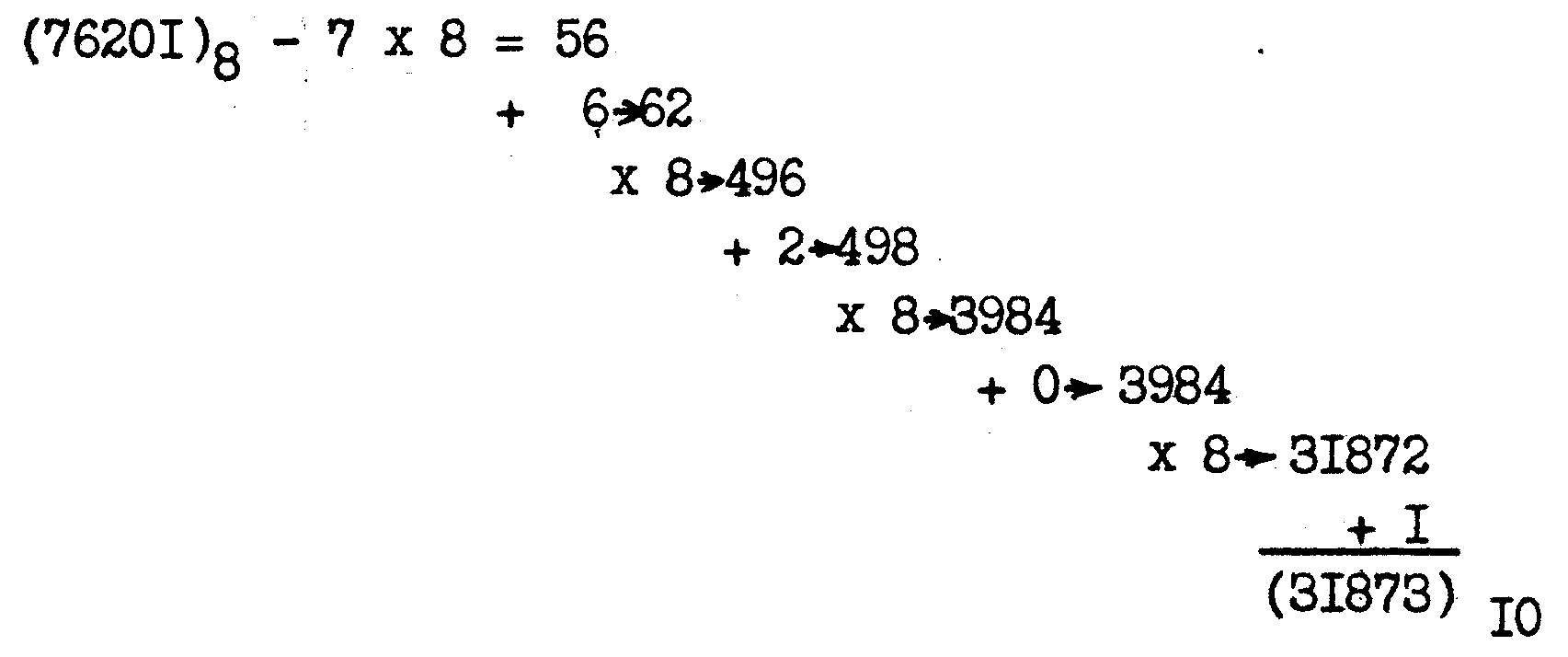
Перевод правильных дробей

Исходное число Aq₁ записанное в новой системе счисления с основанием q₂ по схеме Горнера будет иметь вид:

A(q₂)=(q₂^-1( b_-1 + q₂^-1(b_-2 + … + q₂^-1(b_-(s-1)+q₂^-1b_-s))…) (1.7)

Если правую часть выражения (1.7) умножить на q₂, то найдем новую неправильную дробь, в целой части которой будет число b_-1 . Умножив затем оставшуюся дробную часть на величину основания q₂ получим дробь, в целой части которой будет b_-2.

Повторяя процесс умножения S раз, найдем все S цифр чис­ла в новой системе счисления. При этом все действия должны выпол­няться по правилам q₁-арифметики и, следовательно, в целой части получающихся дробей будут проявляться эквиваленты цифр новой системы счисления, записанные в исходной системе счисления.

Пример: Перевести десятичную дробь А=0,625 в двоичную систему счисления ( q₂ = 2)

Решение:

При решении использовать выражения по схеме Горнера, и с каждым шагом стирать q₂^-1 для удобства восприятия процесса.

	0, x	625 2
b-1	1, x	250 2
b-2	0, x	500 2
b-3	1, x	000 2
b-4	0,	000

Ответ : A₍₂₎=0,1010₍₂₎