Завдання з теорії ймовірностей і математичної статистики
Задача 1
Студент одержав на іспит п питань, з яких вивчив т. На іспиті він одержав k питань. Для складання іспиту студент повинен відповісти на l питань. Знайти ймовірність того, що студент складе іспит.
№ варіанту |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
k |
6 |
4 |
6 |
7 |
6 |
4 |
8 |
6 |
6 |
6 |
n |
60 |
65 |
70 |
75 |
80 |
85 |
90 |
95 |
100 |
105 |
m |
55 |
64 |
64 |
70 |
75 |
80 |
86 |
90 |
95 |
100 |
l |
4 |
3 |
2 |
3 |
4 |
4 |
5 |
6 |
5 |
3 |
Задача 2
Ймовірності
того, що потрібна для складання деталь
знаходиться у першому, другому, третьому
або четвертому ящиках відповідно
дорівнюють:
.
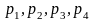Знайти ймовірність того, що деталь
міститься тільки в двох ящиках.
№ варіанту |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
0.2 |
0.3 |
0.3 |
0.8 |
0.2 |
0.7 |
0.5 |
0.9 |
0.6 |
0.7 |
|
0.4 |
0.5 |
0.4 |
0.1 |
0.5 |
0.5 |
0.4 |
0.1 |
0.2 |
0.2 |
|
0.7 |
0.6 |
0.5 |
0.4 |
0.6 |
0.6 |
0.7 |
0.2 |
0.7 |
0.4 |
|
0.5 |
0.2 |
0.8 |
0.5 |
0.8 |
0.8 |
0.9 |
0.5 |
0.4 |
0.6 |
Задача 3
У міську спеціалізовану лікарню поступає у середньому а % хворих з різними формами інфекції, б % з захворюваннями серцево-судинної системи та с % з захворюваннями нервової системи. Ймовірність повного одуження хворого на інфекційні форми т, на захворювання серцево-судинної системи - т та захворювання нервової системи - р. Хворий, який поступив до лікарні одужав. Знайти ймовірність того, що цей хворий мав:
а) інфекційне захворювання;
б) захворювання серцево-судинної системи;
в) захворювання нервової системи.
№ варіанту |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
т |
0,90 |
0,95 |
0,85 |
0,96 |
0,88 |
0,92 |
0,89 |
0,93 |
0,94 |
0,91 |
п |
0,50 |
0,51 |
0,55 |
0,59 |
0,60 |
0,61 |
0,45 |
0,57 |
0,63 |
0,65 |
р |
0,20 |
0,50 |
0,40 |
0,50 |
0,30 |
0,25 |
0,30 |
0,15 |
0,35 |
0,35 |
a |
80 |
82 |
84 |
86 |
78 |
76 |
74 |
84 |
72 |
81 |
b |
15 |
11 |
10 |
12 |
15 |
13 |
12 |
12 |
19 |
12 |
c |
5 |
7 |
6 |
2 |
7 |
11 |
14 |
4 |
9 |
7 |
Задача 4
Контрольний тест складається з п питань. На кожне питання пропонується 4 варіанта відповіді, серед яких тільки один правильний. Знайти ймовірність складання тесту для непідготовленого студента, якщо він відповість більше ніж на т питань.
№ варіанту |
п |
т |
№ варіанту |
п |
т |
1 |
5 |
3 |
6 |
8 |
6 |
2 |
6 |
4 |
7 |
7 |
5 |
3 |
7 |
4 |
8 |
6 |
3 |
4 |
8 |
5 |
9 |
9 |
6 |
5 |
9 |
5 |
10 |
5 |
4 |