Модель Окумури-Хата

Обмеження f=150-1500 МГЦ h_BS=30..200 м h_MS=1..10м R=1..20 км

L=69.55+26*log₁₀(f)-13.82*log₁₀(h_BS-a(h_MS)+(44.9_6.55*log₁₀(h_BS)*log₁₀ (R) [ dB]

F- частота носійної( МГц)

h_BS , h_MS висоти антен базової та мобільної станцій [ м]

R- відстань між базовою та мобільною станціями [км]

Поправочний коефіцієнт a(h_MS) залежить від типу місцевості.

Для малих та середніх міст

a(h_MS)=1.1*log10(f)-0.7)* h_MS-(1.56*log10(f)-0.8)

Для великих міст

a(h_MS)=3.2*[log₁₀(11.75* h_MS)]²-4.97 при f>400 МГц

a(h_MS)=8.29*[log₁₀(1.54* h_MS)]²-1.1 при f<200 МГц

В типових приміських районах величина

L_P=L-2*[log₁₀(f/28)]²-5.4

В сільский місцевості

L_c=L-4.78*[log₁₀(f)]²+18.33*log₁₀(f)-40.94

Трафик в системах множественного доступа

Ограничивать количество обслуживаемых абонентов числом каналов связи представляется нерациональным, поскольку вероятность одновременного выхода на связь всех абонентов системы обычно мала. Следовательно, при наличии К каналов связи система, в принципе, способна об­служивать более К абонентов, хотя существует вероятность того, что в некоторых случаях абоненты не получат доступа, и эта ве­роятность тем больше, чем больше число абонентов по сравне­нию с количеством каналов связи. Отсюда вытекает двуединая задача, условия которой могут быть сформулированы следую­щим образом: сколько абонентов может обслужить система, имеющая фиксированное количество каналов связи при заданной вероятности отказа в доступе, либо - какое количество каналов связи в системе необходимо для обслуживания заданного числа абонентов при фиксированной вероятности отказа в доступе. Ре­шение поставленной задачи основано на положениях теории массового обслуживания. Действительно, СМР по своей сути яв­ляется примером системы массового обслуживания, т.е. системы со случайным потоком заявок (вызовов), случайной продолжи­тельностью обслуживания (сеанса связи) и конечным числом ка­налов обслуживания (связи).

Наиболее общими характеристиками случайного потока вызовов являются средняя частота их поступления  , измеряе­мая числом вызовов в единицу времени (например, число вызовов/час), и средняя продолжительность сеанса связи Т, выра­жаемая в единицах времени. Произведение   определяет средний трафик (интенсивность трафика, поток нагрузки, общую нагрузку на канал связи), измеряемый в эрлангах. Следует отметить, что характеристики на­грузки на канал связи   и Т обычно оценивают на интервале наибольшей загруженности системы, т.е. в ЧНН.

Число вызовов в течение фиксированного времени t пред­ставляет собой дискретную случайную величину, обычно описы­ваемую распределением Пуассона: 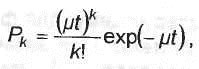 где Рк - вероятность поступления к вызовов за время t. Про­должительность сеанса связи (длительность занятости одного канала)   является непрерывной случайной величиной, плот­ность вероятности которой обычно принимается экспоненциаль­ной (Т - как указывалось, среднее значение  )

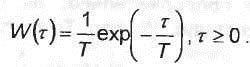
В зависимости от того, как ведет себя система, не располагающая свободными каналами на момент поступления новой заявки, различают следующие ее модели:

• система с ограниченным временем ожидания (модель Эрланга А), согласно которой вызов при отсутствии свободного канала ставится в очередь и по истечении фиксированного времени Т - если за это время ни один из занятых каналов не освободился - аннулируется;

• система с отказами, т.е. вызовы, пришедшие в момент от­сутствия свободных каналов, аннулируются (модель Эрланга В);

• система с ожиданием, т.е. вызовы становятся в очередь и могут ожидать освобождения канала неопределенно долгое время (модель Эрланга С).

При оценке абонентской емкости системы подвижной ра­диосвязи обычно применяется модель Эрланга В, для которой вероятность отказа определяется соотношением:

Данная формула, определяющая вероятность отказа в доступе к системе, достаточно громоздка для непосредственного применения. На практике для расчета допустимой нагрузки в эрлангах для системы связи с К каналами при заданной вероятности блокировки Рв используют ее представление либо в виде графика, либо в виде таблицы.

Алгоритм применения соотношения для Рв, либо его табу­лированного представления сводится к следующему: для фикси­рованного количества каналов связи в системе К и заданного значения вероятности отказа Рв находится трафик А, который может быть обслужен в рассматриваемых условиях. Так, при К = 30 и вероятности отказа Рв = 0,02 система связи может об­служить нагрузку на все каналы, равную 21,93 эрланга. Если же предположить, что в час пик любой абонент системы производит в среднем 2 вызова со средней продолжительностью связи 5 минут, то трафик на один канал составит 1/6 эрл. Тогда системой может быть обслужено число заявок, равное  , которым и оценивается реальная абонентская емкость системы.