
- •Организация и функции статистических служб
- •Понятие о статистической информации
- •Статистическое наблюдение
- •Принципы построения статистических группировок
- •Вариационные ряды
- •Графическое отображение вариационных рядов
- •Пример 3.1.
- •Обобщающие статистические показатели
- •1. Средние величины
- •1.1 Средние степенные величины
- •1.2 Средние структурные величины
- •2. Анализ вариационных рядов
- •2.1. Показатели вариации
- •2.1.1. Свойства дисперсии
- •2.1.2 Вариация альтернативного признака
- •2.2. Виды дисперсий в совокупности, разделенной на части. Правило сложения дисперсий
- •3. Моменты распределения Показатели формы распределения
- •3.1. Моменты распределения
- •3.2. Показатели формы распределения
- •3.3. Теоретические кривые распределения
- •4. Выборочное наблюдение в статистике
- •4.1. Закон больших чисел и предельные теоремы
- •Выборочное наблюдение
- •4.2. Ошибка выборки для альтернативного признака
- •4.3 Определение необходимой численности выборки
- •4.4 Формы организации выборочного наблюдения
- •5. Статистические методы изучения взаимосвязи социально-экономических явлений
- •5.1 Регрессионный анализ
- •5.2 Корреляционный анализ
- •6. Ряды динамики
- •6.1 Анализ динамических рядов
- •6.2 Методы анализа тенденций рядов динамики
- •6.3 Сезонные колебания
- •6.4. Статистические методы прогнозирования экономических показателей
- •6.4.1. Прогнозирование на основе экстраполяции тренда
- •8.4.2. Выбор наилучшего тренда при прогнозировании
- •7. Экономические индексы
- •7.1 Общие индексы количественных показателей
- •8.2 Общие индексы качественных показателей
- •7.3 Индексы переменного и фиксированного состава. Индекс структурных сдвигов
- •Приложение Значение критерия Пирсона χ2
- •Приложение
- •Приложение
- •Окончание приложения
1. Средние величины
Средняя величина является обобщающей характеристикой совокупности однотипных явлений по изучаемому признаку. Средняя величина должна вычисляться с учетом экономического содержания определяемого показателя.
Все виды средних делятся на:
степенные (аналитические, порядковые) средние (арифметическая, гармоническая, геометрическая, квадратическая);
структурные (позиционные) средние (мода и медиана) – применяются для изучения структуры рядов распределения.
1.1 Средние степенные величины
Средняя степенная (при различной величине k) определяется:
 (1.1).
(1.1).
Таблица 1.1 - Виды средних степенных величин
k |
Наименование средней |
Формула средней |
Когда используется |
1 |
Средняя арифметическая простая (невзвешенная) |
где xi
– i-й вариант осредняемого признака
( |
Используется, когда расчет осуществляется по несгруппированным данным |
1 |
Средняя арифметическая взвешенная |
где fi – частота повторяемости i-го варианта |
Используется, когда данные представлены в виде рядов распределения или группировок |
-1 |
Средняя гармоническая взвешенная |
|
Используется, когда известны индивидуальные значения признака и веса W за ряд временных интервалов |
-1 |
Средняя гармоническая невзвешенная |
|
Используется в случае, когда веса равны |
0 |
Средняя геометрическая невзвешенная |
|
Используется в анализе динамики для определения среднего темпа роста |
0 |
Средняя геометрическая взвешенная |
|
|
2 |
Средняя квадратическая невзвешенная |
|
Используется при расчете показателей вариации |
2 |
Средняя квадратическая взвешенная |
|
В статистическом анализе также применяются степенные средние 3-го и более высоких порядков.
Правило мажорантности средних: с ростом показателя степени значения средних возрастают.
![]() (1.10)
(1.10)
Средняя прогрессивная – средняя для “лучших” значений признака.
Свойства средней арифметической
Средняя арифметическая постоянной величины равна самой величине.
Если все варианты xi увеличить (уменьшить) на одно и тоже число c,
 увеличится (уменьшится) на то же число.
увеличится (уменьшится) на то же число.
 . (1.11)
. (1.11)
Если все варианты xi увеличить (уменьшить) в одно и то же число раз k, увеличится (уменьшится) в то же число раз.
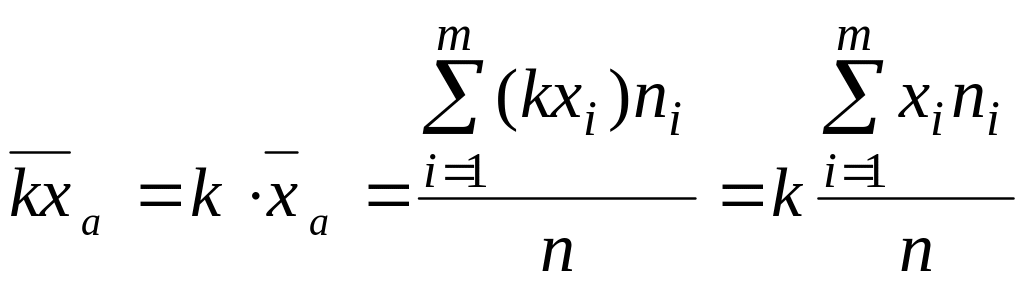 . (1.12)
. (1.12)
Средняя арифметическая отклонений вариантов от средней арифметической равна 0.
![]() . (1.13)
. (1.13)
По
свойству 2 при
![]() :
:
![]() .
.
Средняя арифметическая алгебраической суммы признаков равна такой же сумме средней арифметической этих признаков.
![]() . (1.14)
. (1.14)
Если ряд состоит из нескольких групп, общая средняя равна средней арифметической групповых средних, причем весами являются объемы группы.
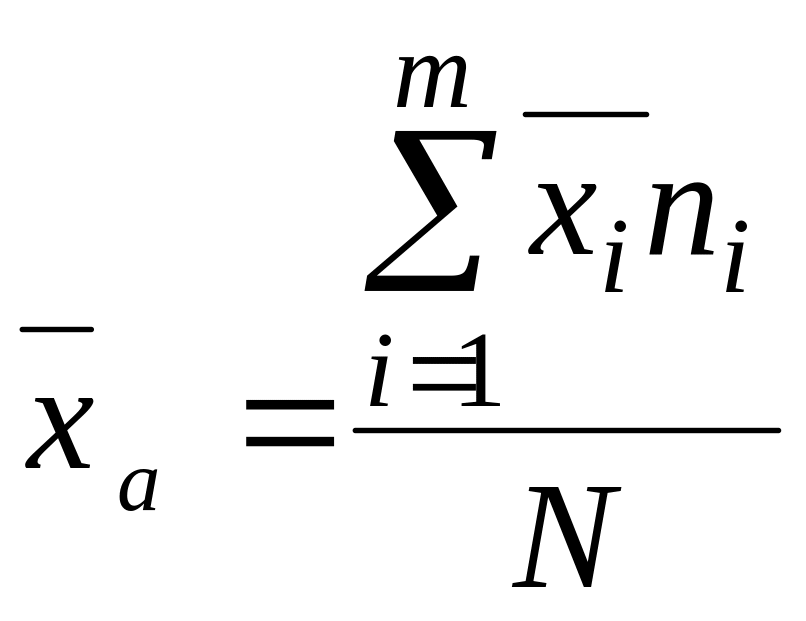 , (1.15)
, (1.15)
где
![]() – средняя арифметическая группы i;
– средняя арифметическая группы i;
N
– общий объем ряда (![]() );
);
ni
– объем группы i
(![]() ).
).
 . (1.16)
. (1.16)

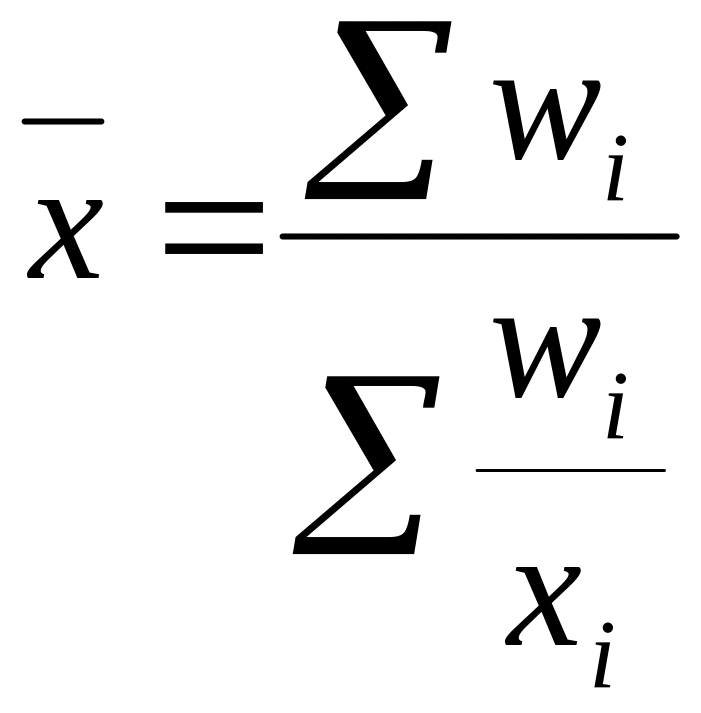 (1.4), где
(1.4), где  (1.9)
(1.9)