
- •Организация и функции статистических служб
- •Понятие о статистической информации
- •Статистическое наблюдение
- •Принципы построения статистических группировок
- •Вариационные ряды
- •Графическое отображение вариационных рядов
- •Пример 3.1.
- •Обобщающие статистические показатели
- •1. Средние величины
- •1.1 Средние степенные величины
- •1.2 Средние структурные величины
- •2. Анализ вариационных рядов
- •2.1. Показатели вариации
- •2.1.1. Свойства дисперсии
- •2.1.2 Вариация альтернативного признака
- •2.2. Виды дисперсий в совокупности, разделенной на части. Правило сложения дисперсий
- •3. Моменты распределения Показатели формы распределения
- •3.1. Моменты распределения
- •3.2. Показатели формы распределения
- •3.3. Теоретические кривые распределения
- •4. Выборочное наблюдение в статистике
- •4.1. Закон больших чисел и предельные теоремы
- •Выборочное наблюдение
- •4.2. Ошибка выборки для альтернативного признака
- •4.3 Определение необходимой численности выборки
- •4.4 Формы организации выборочного наблюдения
- •5. Статистические методы изучения взаимосвязи социально-экономических явлений
- •5.1 Регрессионный анализ
- •5.2 Корреляционный анализ
- •6. Ряды динамики
- •6.1 Анализ динамических рядов
- •6.2 Методы анализа тенденций рядов динамики
- •6.3 Сезонные колебания
- •6.4. Статистические методы прогнозирования экономических показателей
- •6.4.1. Прогнозирование на основе экстраполяции тренда
- •8.4.2. Выбор наилучшего тренда при прогнозировании
- •7. Экономические индексы
- •7.1 Общие индексы количественных показателей
- •8.2 Общие индексы качественных показателей
- •7.3 Индексы переменного и фиксированного состава. Индекс структурных сдвигов
- •Приложение Значение критерия Пирсона χ2
- •Приложение
- •Приложение
- •Окончание приложения
4.1. Закон больших чисел и предельные теоремы
Под законом больших чисел в широком смысле понимается общий принцип, согласно которому, по формулировке академика Колмогорова, совокупное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая. Или иначе: При большом числе случайных величин их средней результат перестает быть случайным и может быть предсказан с большой степенью определенности.
Под законом больших чисел в узком смысле понимается ряд математических теорем, в каждой из которых для тех или иных условий устанавливается факт приближения средних характеристик большого числа испытаний к некоторым определенным постоянным.
Неравенство Чебышева: для любой случайной величины, имеющей математическое ожидание M(X) и дисперсию D(X) справедливо:
![]() , (4.1)
, (4.1)
или
![]() , (4.2)
, (4.2)
Если
формула (6.1) устанавливает верхнюю
границу рассматриваемого события, то
(4.2) – нижнюю границу вероятности события,
состоящего в том, что отклонения значения
случайной величины от математического
ожидания не превысит (не будет менее)
величины![]() ,
где
,
где
![]() – достаточно малая величина.
– достаточно малая величина.
В
приложении к выборочному методу
неравенство Чебышева может быть
сформулировано так: при неограниченном
увеличении числа наблюдений (![]() )
в генеральной совокупности с ограниченной
дисперсией с вероятностью близкой к
единице можно ожидать, что отклонение
выборочной средней (
)
в генеральной совокупности с ограниченной
дисперсией с вероятностью близкой к
единице можно ожидать, что отклонение
выборочной средней (![]() )
от генеральной средней
)
от генеральной средней
![]() будет сколь угодно мало:
будет сколь угодно мало:
![]() при
.
Эту вероятность в теореме А.М. Ляпунова
(1901г.) используют для определения ошибки
наблюдений.
при
.
Эту вероятность в теореме А.М. Ляпунова
(1901г.) используют для определения ошибки
наблюдений.
![]() , (4.3)
, (4.3)
где
![]() -
нормированная формула Лапласса.
-
нормированная формула Лапласса.
![]() – средняя
квадратическая или стандартная ошибка
выборки.
– средняя
квадратическая или стандартная ошибка
выборки.
 . (4.4)
. (4.4)
Пусть надо измерить некоторою величину, истинное значение которой равно a. Пусть результат каждого измерения – случайная величина Xi (i=1,2,…,n). Если при измерениях отсутствует систематические погрешности, то M(Xi)=a при любом i. Тогда средняя арифметическая результатов и измерений сходится по вероятности к истинному значению a.
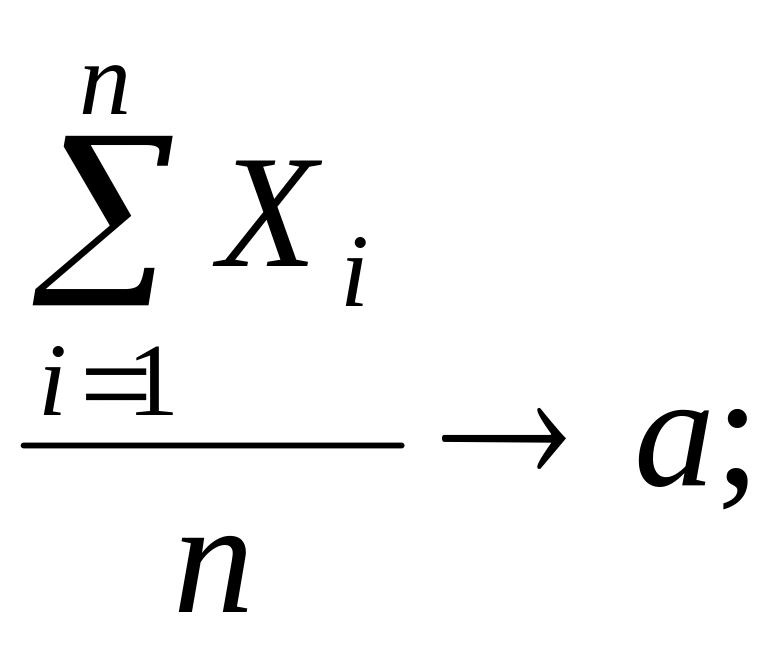 (4.5)
(4.5)
Дисперсия средней случайной величины Xi равна
 (4.6)
(4.6)
Среднее квадратическое отклонение ошибок выборки
![]() , (4.7)
, (4.7)
![]() . (4.8).
. (4.8).
Зная
выборочную среднюю
![]() и предельную ошибку выборки
и предельную ошибку выборки
![]() можно определить границы, в которых
размещена генеральная средняя
.
можно определить границы, в которых
размещена генеральная средняя
.
Величина средней квадратической ошибки простой случайной повторной выборки может быть определена по формуле:
![]() , (4.9)
, (4.9)
т.е. чем больше вариация признака в генеральной совокупности, тем больше ошибка выборки.
Величину
![]() называют предельной
ошибкой
для определения значения вероятности.
Если требуется оценить среднюю генеральной
совокупности
с вероятностью 0,9545, то надо получить
значение выборочной средней из
соотношения
называют предельной
ошибкой
для определения значения вероятности.
Если требуется оценить среднюю генеральной
совокупности
с вероятностью 0,9545, то надо получить
значение выборочной средней из
соотношения
![]() (функция Лапласа).
(функция Лапласа).
Для
выборки объема
![]() предельная ошибка
предельная ошибка
![]() может быть определена из соотношения
может быть определена из соотношения
![]() .
.
t |
1,00 |
1,96 |
2,00 |
2,58 |
3,00 |
F(t) |
0,683 |
0,9500 |
0,9545 |
0,9901 |
0,9973 |
![]() – это предел
возможной ошибки (правило «трех сигм»).
– это предел
возможной ошибки (правило «трех сигм»).
Формула предельной ошибки выборки используется не только для оценки пределов, в которых находится изучаемый признак в генеральной совокупности, но и для определения необходимого объема выборки при заданной ее ошибке. Третий тип задач, которые могут быть решены с использованием предельной ошибки выборки, – это определение вероятности, с которой можно гарантировать, что ошибка выборки не выйдет за заданные пределы.
Величина
дисперсии генеральной совокупности
![]() принципиально не известна и можно
говорить лишь о ее оценке по результатам
одной выборки.
принципиально не известна и можно
говорить лишь о ее оценке по результатам
одной выборки.
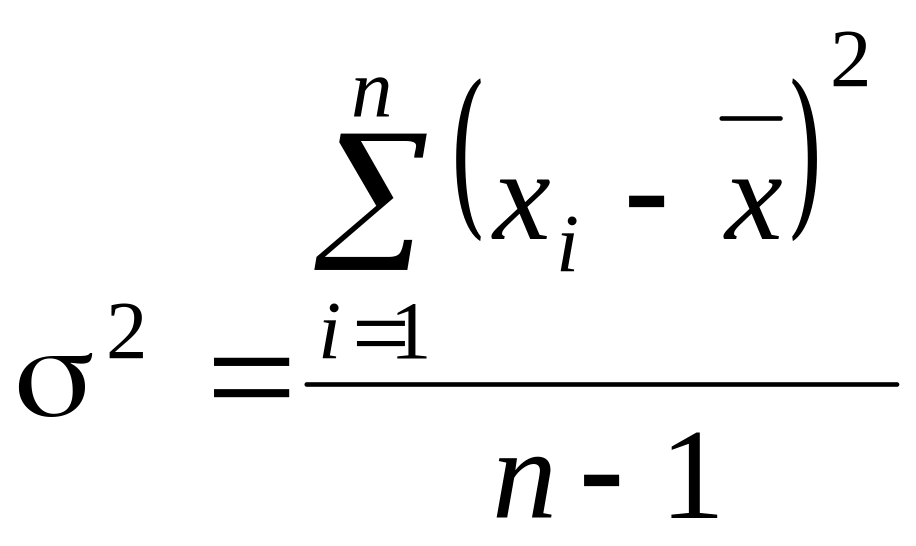 –для простой
случайной выборки.
–для простой
случайной выборки.
При
![]() ,
поправка
,
поправка
![]() становится
становится
![]() 3,5% (30/(30-1)), поэтому ею можно пренебречь.
3,5% (30/(30-1)), поэтому ею можно пренебречь.
