10. Оценка качества работы системы с использованием квадратичной интегральной оценки

Квадратичная интегральная оценка качества используется в случае колебательных переходных процессов. Вычисление интеграла следует вести с применением рекуррентных формул. При этом передаточная функция замкнутой скорректированной системы по ошибке от управляющего воздействия представляется в виде дробно-рациональной функции.

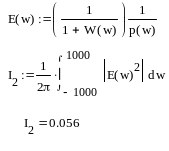
Так как интеграл конечный, то колебания в системе затухающие.

11. Математическая модель скорректированной системы

При составлении математической модели скорректированной системы необходимо написать передаточную функцию разомкнутой желаемой САУ Wж(p).

Рис. 14. Математическая модель САУ.

Запишем уравнения переменных состояний:

X0=1

X5=X0-X6

X1=17*X5

X2’=10*X1

X3’=-100*X3+100*X2

X4’=-100*X4+100*X3

X5’=-100*X5+100*X4

Для построения переходного процесса воспользуемся пакетом SyAn.

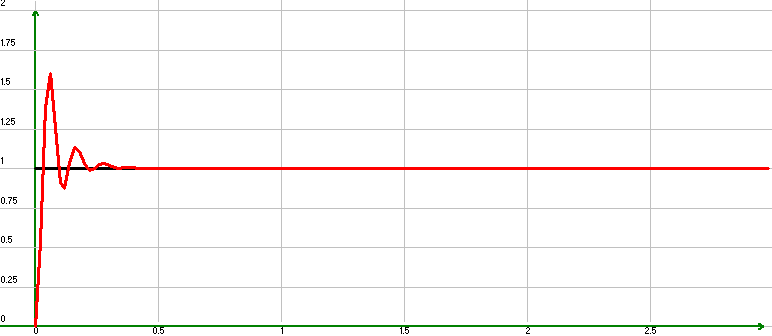
Рис.15. Переходный процесс при подаче g(t)=1(t).

Время регулирования составляет 0,19 секунд, а перерегулирование 16%.

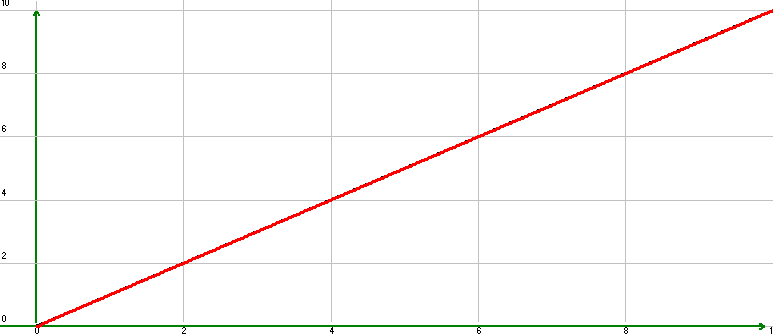
Рис.16. Переходный процесс при подаче g(t)=1(t)*t.

12. Определение ошибки от возмущающего воздействия

Ошибка от возмущающего воздействия определяется по формуле:

;

.

В результате вычисления получаем, что ошибка от возмущающего воздействия при p стремящемся к нулю очень мала.

Заключение

В курсовой работе в соответствии с выбранной функциональной схемой рассмотрели анализ и синтез САУ и составили передаточные функции системы. Построили частотные характеристики. По методу Найквиста проверили устойчивость работы системы и определили, что при начальных параметрах системы она является неустойчивой. Используя логарифмические частотные характеристики определили параметры корректирующего устройства по методу Солодовникова. При помощи корректирующего устройства добились того, чтобы система стала устойчивой и обеспечили требуемые показатели качества системы при подаче на вход САУ управляющих воздействий. В ходе работы был построен график переходного процесса при единичном управляющем воздействии по методу трапеций. Время регулирования в скорректированной системе около 0,3 секунд, перерегулирование 16%, скоростная ошибка равна 0.01, а также ошибка от единичного возмущающего воздействия равна 0,005.