7. Построение границы устойчивости по методу d – разбиения

D – разбиение производится относительно параметра Тм. Для этого решим характеристическое уравнение замкнутой системы относительно интересующих нас параметров.

Передаточная функция разомкнутой САУ:

;

;

Характеристическое уравнение замкнутой системы:

;

;

;

;

.

Приравняем к нулю.

;

Построим кривую D-разбиения.

I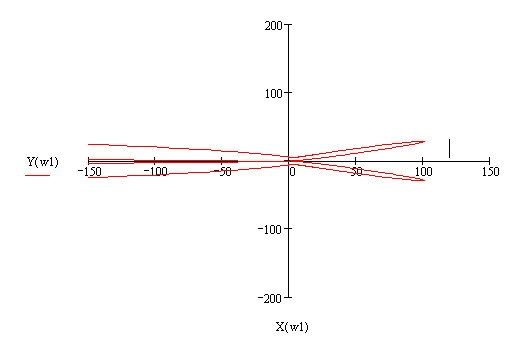

Рис. 7. Кривая D-разбиения

Проверим область I на устойчивость по Найквисту, взяв точку X= 50 и Y = 0.

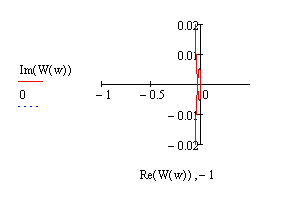
Область I – область не устойчивости.

8. Определение параметров корректирующего устройства.

8.1. Построение желаемой логарифмической амплитудно-частотной характеристики.

Показатели качества регулирования:

ск = 0,015 t рег = 0,15 с пер = 20 %

Частота среза определяется с помощью номограммы В.В.Солодовникова. По перерегулированию определяем Pmax=1.3, тогда можем найти частоту среза и по ней определить требуемые показатели качества системы регулирования.

Для систем с частотами среза _ср=1100 Hz достаточные запасы по модулю и фазе принимают следующие значения:

Требуемый коэффициент усиления системы найдём из формулы:

Объединив все параметры желаемой САУ, находим передаточную функцию и построим желаемую ЛАХ:

.

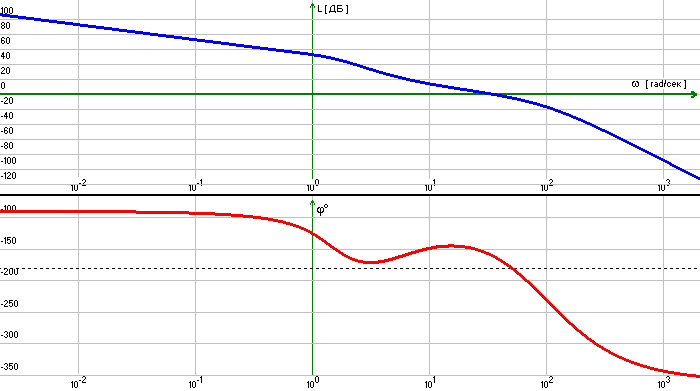
Рис. 8. ЛАХ желаемой САУ.

8.2. Определение параметров корректирующего устройства.

Построим амплитудно-частотную характеристику корректирующего устройства по правилу:

График представлен на рис. 9. Запишем передаточную функцию корректирующего устройства:

.

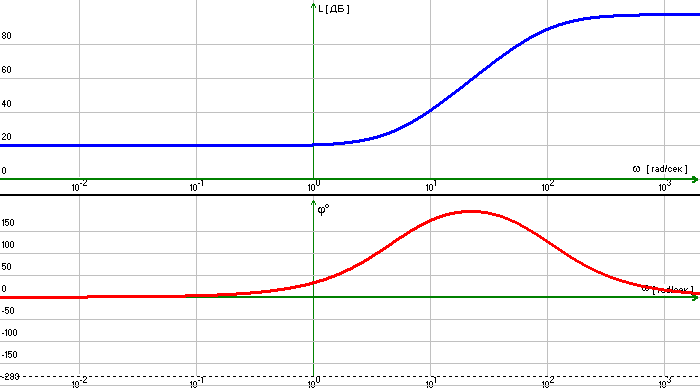
Рис. 9. ЛАХ корректирующего устройства.

При схемной реализации корректирующей цепи передаточную функцию корректирующего устройства целесообразно представить в виде совокупности ряда табличных цепей, т.е. корректирующую цепь разобьем на 3 простых звена. Задаваясь одним параметром схемы через соответствующие формулы определяем параметры всей схемы.

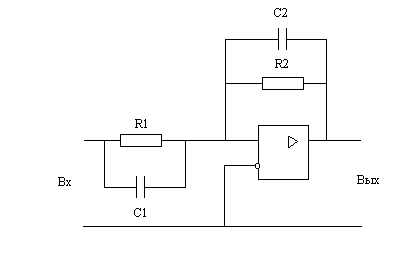
Рис. 10. Модель корректирующего устройства.

1. .

T1=0,2; R1=1,6 кОм; R2=16 кОм; C1=12,5 мкФ; T2=0,02; C2=1,25 мкФ.

2,3. .

T1=0,2; R1=1,6 кОм; R2=1,6 кОм; C1=125 мкФ; T2=0,02; C2=12,5 мкФ.

9. Построение переходного процесса

Для построения переходного процесса возьмём передаточную функцию скорректированной системы:

.

Передаточная функция замкнутой системы:

;

.

Построим график вещественной функции (рис.11):

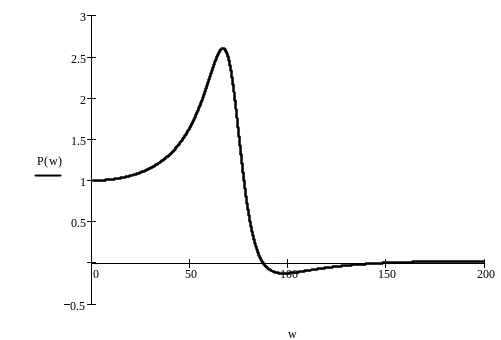
Рис. 11. График вещественной функции

По методу трапеций построим переходной процесс. Разобьем вещественную функцию на три трапеции и для каждой трапеции запишем h-функцию.

Таблица 9.1.

Трапеция 1				Трапеция 2				Трапеция 3
di=45 0i=65 10.65				di=65 0i=85 10.68				di=85 0i=125 10.68
h0i=-1.6				h0i=2.73				h0i= -0,13
tтабл, с	tист, с	hi	hdihi	tтабл, с	tист, с	hi	hdihi	tтабл, с	tист, с	hi	hdihi
0,4	0,133	0,215	-0,344	0,4	0,018	0,215	0,587	0,4	0,013	0,215	-0,028
1,2	0,267	0,6119	-0,979	1,2	0,055	0,6119	1,670	1,2	0,038	0,6119	-0,080
2,4	0,400	1,0276	-1,644	2,4	0,109	1,0276	2,805	2,4	0,075	1,0276	-0,134
3,6	0,533	1,1678	-1,868	3,6	0,164	1,1678	3,188	3,6	0,113	1,1678	-0,152
4	0,667	1,1627	-1,860	4	0,182	1,1627	3,174	4	0,125	1,1627	-0,151
6,8	0,800	0,9335	-1,494	6,8	0,309	0,9335	2,548	6,8	0,213	0,9335	-0,121
11,2	0,933	1,0387	-1,662	11,2	0,509	1,0387	2,836	11,2	0,350	1,0387	-0,135
14,8	1,067	0,9862	-1,578	14,8	0,673	0,9862	2,692	14,8	0,463	0,9862	-0,128
21,2	1,200	1,0019	-1,603	21,2	0,964	1,0019	2,735	21,2	0,663	1,0019	-0,130

Просуммировав все три графика, получим переходный процесс.

Таблица 9.2.

t	0	0,4	1,2	2,4	3,6	4	6,8	11,2	14,8	21,2
h	0	0,215	0,612	1,028	1,168	1,163	0,934	1,039	0,986	1,002

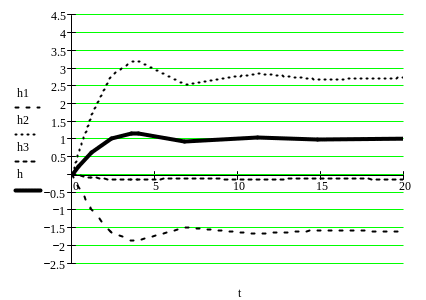
Рис. 12. Переходный процесс

По графику переходного процесса определяем, что время регулирования составляет около 12 секунд, а перерегулирование около 20%.Скоростная ошибка равна: