7.3. Графическое представление статистических распределений

Для наглядности принято использовать следующие формы графического представления статистических распределений: полигоны и гистограммы.

Дискретный ряд изображают в виде полигона. Полигон частот - ломаная линия, отрезки которой соединяют точки с координатами ( _i,  _i); аналогично полигон относительных частот - ломаная, отрезки которой соединяют точки с координатами ( , w_i ).

Интервальный ряд изображают в виде гистограммы. Гистограмма частот есть ступенчатая фигура, состоящая из прямоугольников, основания которых - интервалы длиной , а высоты - плотности частот . Для гистограммы относительных частот высоты прямоугольников - плотности относительных частот . Здесь в общем случае  , однако на практике чаще всего полагают величину h одинаковой для всех интервалов. где i=1, 2, ..., k.

Площадь гистограммы есть сумма площадей ее прямоугольников.

таким образом, площадь гистограммы частот равна объему выборки, а площадь гистограммы относительных частот равна единице.

В теории вероятностей гистограмме относительных частот соответствует график плотности распределения вероятности . Поэтому гистограмму можно использовать для подбора закона распределения генеральной совокупности.

Кумулятивные ряды графически изображают в виде кумуляты. Для ее построения на оси абсцисс откладывают варианты признака или интервалы, а на оси ординат - накопленные частоты Н( ) или относительные накопленные частоты , а затем точки с координатами ( _i ; H( _i )) или ( _i ;  ) соединяют отрезками прямой. В теории вероятностей кумуляте соответствует график интегральной функции распределения .

Замечание 1. Если в статистическом исследовании исходным является статистическое распределение в виде интервального ряда (сгруппированные данные), а исходный вариационный ряд недоступен, то точное расположение отдельных вариант, попавших в каждый из интервалов, неизвестно. Только выбирая в качестве аргумента эмпирической функции распределения правую границу интервала (x_i-1-x_i), мы уверены, что все варианты, попавшие в этот интервал, будут учтены (просуммированы) в значении накопленной частоты (накопленной относительной частоты), соответствующей этому интервалу.

Поэтому в случае интервального ряда значения и H(x) точно определены лишь для правой границы интервала: x = x_i. В остальных точках интервала x_i-1 < x < x_i значения и H(x) можно задать лишь приближенно. Примером может служить кумулята, отрезки прямых которой представляют собой выраженную в графической форме линейную интерполяцию значений и H(x) на интервале x_i-1 <x< x_i .

Замечание 2. В случае дискретного ряда использовать кумуляту для изображения и H(x) можно лишь условно, для наглядности. Более корректным является изображение эмпирической функции распределения , а также H(x) по аналогии с теоретической функцией распределения дискретной случайной величины (рис. 3) ступенчатым графиком - отрезками прямых, параллельных оси абсцисс; длины отрезков - h_i = x_i - x_i-1 , расстояния от отрезков до оси абсцисс - , или H(x_i).

Пример 44. Имеется распределение 80 предприятий по числу работающих на них (чел.):

	150	250	350	450	550	650	750
	1	3	7	30	19	15	5	.

Построить полигон распределения частот.

Решение. Признак Х - число работающих (чел.) на предприятии. В данной задаче признак Х является дискретным. Поскольку различных значений признака сравнительно немного - k = 7, применять интервальный ряд для представления статистического распределения нецелесообразно (в прикладной статистике в подобных задачах часто используют именно интервальный ряд). Ряд распределения - дискретный. Построим полигон распределения частот (рис. 28).

Рис. 28

Пример 45. Дано распределение 100 рабочих по затратам времени на обработку одной детали (мин):

xi-1-xi	22-24	24-26	26-28	28-30	30-32	32-34
	2	12	34	40	10	2	.

Построить гистограмму частот.

Решение. Признак Х - затраты времени на обработку одной детали (мин). Признак Х - непрерывный, ряд распределения - интервальный. Построим гистограмму частот (рис. 29), предварительно определив (k = 6) и плотность частоты .

xi-1-xi	22-24	24-26	26-28	28-30	30-32	32-34
	1	6	17	20	5	1	.

Рис. 29

Пример 46. В распределении, данном в примере 44, найти накопленные частоты H( _i ) и построить кумуляту.

Решение. Используем значения Н(х): H(x₁)=0, H(x_i)=H(x_i-1)+m_i-1 (i=2, 3, ¼, k+1, k=7).

i	1	2	3	4	5	6	7	8
xi	150	250	350	450	550	650	750	850
mi	1	3	7	30	19	15	5	0
H( i )	0	0+1=1	1+3=4	4+7=11	11+30=41	41+19=60	60+15=75	75+5=80

На рис. 30 показана кумулята распределения предприятий по числу работающих (чел.).

Пример 47. В распределении, данном в примере 45, составить эмпирическую функцию распределения и построить кумуляту относительных частот.

Решение. Используем значения Н(х): H(x₀)=0, H(x_i)=H(x_i-1)+m_i (i=1, 2, ¼, k, k=6). Проверка: 1.

i	0	1	2	3	4	5	6
xi-1-xi	-¥-22	22-24	24-26	26-28	28-30	30-32	32-34
mi	0	2	12	34	40	10	2
H( i )	0	0+2=2	2+12=14	14+34=48	48+40=88	88+10=98	98+2=100
	0	0,02	0,14	0,48	0,88	0,98	1

Построим кумуляту распределения (рис. 31).

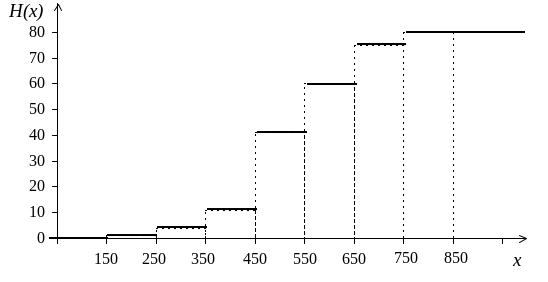
Рис. 30

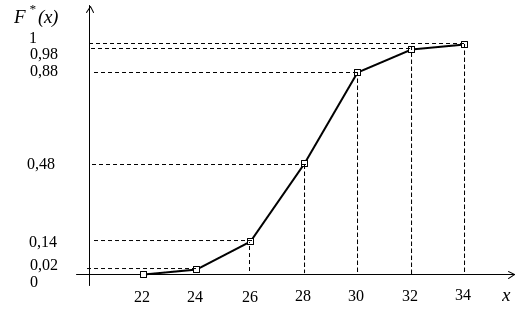
Рис. 31