6.2. Неравенство Чебышева

П.Л. Чебышев в 1846 г. доказал неравенство, позволяющее оценивать вероятность тех или иных отклонений случайной величины Х от ее математического ожидания .

Вероятность того, что отклонение случайной величины Х от ее математического ожидания по абсолютной величине не превзойдет некоторого положительного числа , будет больше разности , то есть

.

Доказательство. Неравенство равносильно неравенству и имеет с ним одинаковую вероятность, то есть

(*)

.

Случайная величина всегда положительная, поэтому для оценки вероятности неравенства можно использовать неравенство Маркова. В результате получим

.

Отсюда согласно равенству (*) будем иметь

.

Но по определению дисперсии , поэтому окончательно получим

,

что и требовалось доказать.

Замечание. Так как события и противоположные, то .

Отсюда получим .

Применяя неравенство Чебышева, получим

.

Это неравенство является другой формой неравенства Чебышева.

Неравенство Чебышева, не используя информации о конкретном виде распределения случайной величины Х, дает лишь грубые оценки для вероятностей событий , или . Например, если оценить вероятность события для нормально распределенной случайной величины Х по неравенству Чебышева, то есть не учитывать нормальности закона распределения Х, то получим

Если сравнить эту величину с точным значением вероятности данного события, которое получается с помощью правила "трех сигм" и равно 0,0027, то видно, что точное значение вероятности в 40 раз меньше ее грубой оценки, полученной на основании неравенства Чебышева.

Пример 42. Вероятность наступления некоторого события в каждом из 700 независимых испытаний равна 0,4. Используя неравенство Чебышева, оценить вероятность того, что событие наступит не менее 250 раз и не более 310.

Решение. Из условия задачи известно: ; ; ; . Требуется оценить . Применим неравенство Чебышева:

.

Найдем и . Известно, что для биномиального закона распределения

и .

Поэтому и .

Теперь найдем . По условию задачи известно, что , вычтем из всех частей этого неравенства , получим , или .

Следовательно, .

Отсюда . Тогда .

.

Но неравенство равносильно неравенству , следовательно, они равновероятны. Поэтому

.

6.3. Теорема Чебышева

Если - независимые случайные величины, имеющие вполне определенные математические ожидания , , а дисперсии их равномерно ограничены, то есть , где С - постоянное число, то при неограниченном увеличении числа случайных величин с вероятностью, близкой к единице, можно утверждать, что отклонение средней арифметической случайных величин от средней арифметической их математических ожиданий по абсолютной величине будет сколь угодно малым, то есть

.

Доказательство. Пусть - независимые случайные величины, имеющие математические ожидания , а дисперсии их равномерно ограниченны, то есть , где С - постоянное число.

Введем случайную величину .

Найдем характеристики этой случайной величины.

.

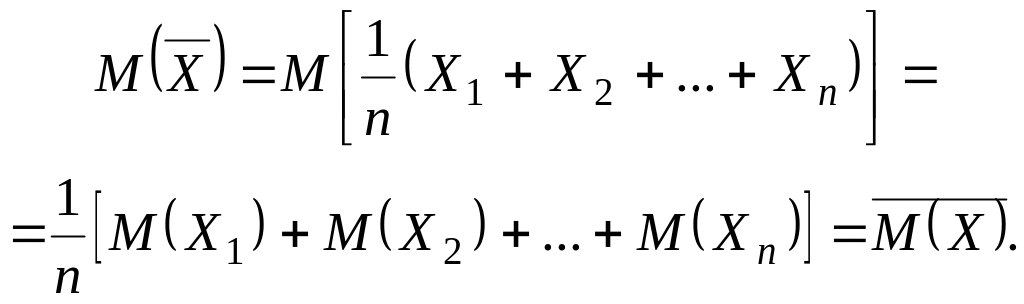
Так как дисперсии равномерно ограничены , то

, или .

Применяя к величине неравенство Чебышева, получим

.

Заменяя и полученными ранее значениями, получим

.

Переходя здесь к пределу при , будем иметь

.

Теорема доказана.

В теореме Чебышева случайные величины X_i, имеют различные математические ожидания. На практике же часто бывает, что случайные величины имеют равные математические ожидания . Если вновь допустить, что дисперсии этих величин ограниченны, то к ним можно применить теорему Чебышева.

Так как , то равенство, вытекающее из теоремы Чебышева, будет иметь вид

.

Сформулируем частный случай теоремы Чебышева: если - независимые случайные величины, имеющие равные математические ожидания ( ), дисперсии которых равномерно ограниченны, то при неограниченном увеличении числа случайных величин с вероятностью, близкой к единице, можно утверждать, что средняя арифметическая этих случайных величин отклоняется от их математического ожидания по абсолютной величине не более, чем на сколь угодно малую положительную величину, то есть .

Кратко последнее равенство можно записать так: . Это означает, что средняя арифметическая случайных величин стремится по вероятности к математическому ожиданию. Таким образом, средняя арифметическая достаточно большого числа случайных величин утрачивает характер случайной величины (вырождается в неслучайную величину). В этом и заключается сущность теоремы Чебышева.

Теорема Чебышева имеет большое практическое применение. Она позволяет получить представление о величине математического ожидания случайной величины, используя среднюю арифметическую. Так, измеряя какой-либо параметр с помощью прибора, не дающего систематической погрешности, можно получить достаточно большое число результатов измерений этого параметра, тогда средняя арифметическая этих измерений, по теореме Чебышева, будет практически мало отличаться от истинного значения параметра.

Пример 43. Дисперсия каждой из 2000 независимых случайных величин не превышает 5. Определить вероятность, с какой можно утверждать, что отклонение средней арифметической этих величин от средней арифметической их математических ожиданий не превзойдет 0,5 по абсолютной величине.

Решение. По условию задачи известно, что

.

Требуется оценить вероятность такого отклонения, то есть

.

Применим теорему Чебышева:

.

.

Следовательно, .