Углы между прямыми и плоскостями

Угол между пересекающимися прямыми.

Любые две пересекающиеся прямые лежат в одной плоскости и образуют четыре угла.

Углом между пересекающимися прямыми называется градусная мера меньшего угла из четырех получившихся.

• Угол между перпендикулярными прямыми равен 90°.

• Угол между параллельными прямыми равен 0°.

У гол между скрещивающимися прямыми.

Две скрещивающиеся прямые не образуют угла в обычном смысле, так как у них нет общей точки.

Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, которые параллельны данным скрещивающимся прямым.

На рисунке а и b – скрещивающиеся прямые. В плоскости  проведем прямую а₁ ǁ а, Оа₁. Угол между прямыми а₁ и b считают углом между скрещивающими прямыми а и b.

Угол между прямой и плоскостью.

Углом между прямой и плоскостью называется угол между этой прямой и ее проекцией на плоскость.

Определим угол между прямой m и плоскостью  (m∩ = О):

1. Из любой точки прямой m опустим перпендикуляр АС на плоскость ;

2. В плоскости  проведем прямую ОС. Прямая ОС называется проекцией прямой m на плоскость ;

3.  АОС является углом между прямой m и плоскостью .

У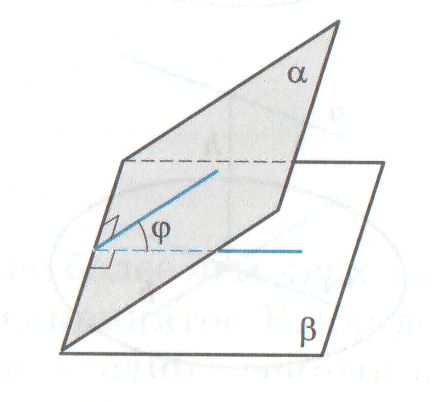 гол между двумя плоскостями.

Для измерения угла между пересекающимися плоскостями надо на линии пересечения этих плоскостей выбрать точку и провести через нее в каждой плоскости прямую, перпенди­кулярную линии пересечения. Угол между этими прямыми и считается углом между плоскостями.

Перпендикулярность плоскостей

Определение.  Две пересекающиеся плоскости перпендикулярны, если угол между ними прямой (90°).

Признак перпендикулярности плоскостей:

Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.

Вопросы и задачи

1. Как определить угол между скрещивающимися прямыми в пространстве?

2. Как определяется угол между прямой и плоскостью?

3. Как вычисляется угол между двумя пересекающимися плоскостями?

4. Как распознать перпендикулярность плоскостей в пространстве?

5. Как признак перпендикулярности плоскостей используется в строительстве?

6. Отрезок АМ является перпендикуляром к плоскости прямоугольника АВСD. Укажите на чертеже угол между прямой МС и этой плоскостью.

7. В параллелограмме АВСD, ВМ – перпендику­ляр к плоскости АВС. Укажите на чертеже угол между прямой МА и плоскостью АВС.

8. 1). Через вершину А параллелограмма АВСD проведен к его плоскости перпендикуляр АМ. Точка М соединена с точками В и D. Укажите угол между плоскостями, проведенными через прямые МА и МD, МА и МВ.

2). Через вершину А прямоугольника АВСD проведен к его плоскости перпендикуляр АМ. Точка М соединена с точкой В. Через прямые МА и МВ проведена плоскость. Укажите линейный угол при ребре АВ.

3). Из вершины А равностороннего треугольника АВС проведен к его плоскости перпендикуляр АМ. Точка М соединена с точками В и С. Через прямые МА и МВ, МА и МС проведены плоскости. Определите градусную меру угла, образованного этими плоскостями.

1 Аксиома – это утверждение не требующее доказательства.

2 Теорема – это утверждение требующее доказательства.