дов наблюдения за окружающей средой потребует дальнейшего развития методов измерений и приборостроения. Электронно­оптические явления в фотоэлектронных процессах и фотосин­тезе займут значительное место в учебных программах и в науч­ных исследованиях. Такие изменения в курсах физики дадут учащимся возможность весьма плодотворно использовать свои знания в дальнейшей практической работе.

Подобные изменения затронут химию, биологию и некото­рые другие прикладные науки. Можно надеяться, что все эти изменения разорвут тесную связь науки, особенно физики, с военной промышленностью. Многие физики испытывают чув­ство вины за то, что развитие ядерной физики привело к созда­нию ядерного оружия. Мы надеемся, что широкое использование возобновляемой энергии также вызовет большие перемены в мире, но эти перемены будут на пользу всему человечеству.

Г лава 2

Основы механики жидкости 2.1. Введение

Преобразование энергии движения жидкости лежит в основе работы гидро-, ветро-, волновых и ряда солнечных энергетиче­ских систем. Чтобы понять принцип работы этих систем, следует рассмотреть основные законы механики: сохранение массы, коли­чества движения (импульса), энергии. Течения, как правило, будем считать несжимаемыми. Термином «жидкость» обознача­ются как собственно жидкости, так и газы. Признаком, отличаю­щим жидкость от твердого тела, является ее неспособность в состоянии равновесия оказывать сопротивление тангенциальным силам (сдвигу). Различие между жидкостью и газом состоит в гораздо большей сжимаемости последнего. Некоторая масса любой жидкости имеет вполне определенный объем, который очень слабо зависит от ее температуры и давления. Объем же, занимаемый некоторой массой газа, сильно зависит от темпера­туры и давления и определяется, в первом приближении, урав­нением состояния совершенного газа (pV — nRT). Если скорость газового потока меньше 100 м/с и нет внешних воздействий, изменяющих его параметры, плотность газа можно считать постоянной. В книге рассматриваются в основном такие случаи.

Во многих приложениях течение жидкости является стацио­нарным (установившимся), когда картина течения (поле тече­ния) не изменяется во времени. В этом случае картину течения удобно представить множеством линий, направление которых в

30

каждой точке течения совпадает с вектором скорости в данной точке. Эти линии называются линиями тока.

Течение может быть ламинарным и турбулентным. Свойства этих течений и различия между ними рассмотрены ниже, в § 2.5, здесь же для примера можно привести струйку дыма, под­нимающуюся в спокойном воздухе с тлеющего фитиля свечи. Сначала струйка дыма поднимается почти строго вертикально, не размываясь. Такое спокойное течение называется ламинар­ным. Потом форма струи искривляется, отдельные ее частицы начинают совершать хаотические перемещения в различные сто­роны. Течение становится турбулентным. Провести точный ра­счет турбулентного течения очень сложно, но часто оказывается достаточным считать его в целом стационарным вязким течением, в котором вязкость обусловлена хаотическим движением частиц.

2. Закон сохранения энергии, уравнение Бернулии

Рассмотрим наиболее важный случай стационарного несжи­маемого течения. В таком течении, как следует из § 2.1, можно выделить трубки тока, т. е. струйки, ограниченные непроницае­мой поверхностью, состоящей из линий тока.

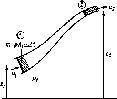
На рис. 2.1 показана трубка тока с начальным сечением на высоте z\ и конечным на гч. Трубка тока достаточно тонкая, чтобы координату г считать постоянной в пределах любого попе­речного сечения.

Рассмотрим течение в контрольном объеме, ограниченном боковой поверхностью трубки тока и двумя поперечными сече­ниями 1 и 2. Через сечение 1 в контрольный объем втекает масса жидкости m = pAiU\kt и столько же жидкости вытекает через сечение 2. Тогда из закона сохранения энергии жидкости в контрольном объеме следует, что потери потенциальной энергии и работа, совершаемая силами давления, в сумме равны увели­чению ее кинетической энергии и потерям энергии на трение. Этот баланс запишем в виде

mg (zi — z₂) + [ OMi) (uiAt) — (P2A2) (u₂A0 ]=4- ^m («2 — m? )+E_f

(2.1)

Здесь сила давления p\A\ совершает работу на расстоянии u\kt (аналогично и для Р2А2), £)— тепловыделение при трении.

В идеальном случае, когда трением можно пренебречь, урав­нение (2.1) принимает вид

(РI /р) + gZi + у И? = (Ра/р) + gZ2 + у «2 (2.2)

или вдоль линии тока

P- + z+£-= const. (2.3)

Pg 2g ^v '

31

Рис. 2.1. Иллюстрация закона сохране- ния энергии для трубки тока

Обе эти формы уравнения сохранения энергии называются уравнением Бернулли.

Сумма членов левой части (2.3) называется полным напо- ром. Полный напор — это пол- ная энергия единицы массы жидкости, которая в общем слу- чае различна в различных точ- ках течения. В частности, кон- станта в (2.3) может изменять-

ся от одной линии тока к другой. Напор имеет размерность дли- ны, т. е. соответствует потенциальной энергии столба жидкости высотой, равной напору.

Уравнения (2.2) и (2.3) справедливы для течений, в которых можно пренебречь вязкостью, сжимаемостью и теплопровод­ностью. В противном случае в уравнение энергии следует ввести члены, учитывающие влияние этих факторов. Вид уравнения энергии для сжимаемой жидкости можно найти в любом учебни­ке по механике жидкости. При малых скоростях, рассматривае­мых в этой книге, оно сводится к виду (2.3). Предположение

об отсутствии теплопроводности означает, в частности, что отсутствует поток тепла через боковую поверхность рассматри­ваемой трубки тока от посторонних источников тепла, поэтому (2.3) справедливо, если в потоке нет источников тепла, что и имеет место в большинстве ветро- и гидроэнергетических уста­новок.

В приемниках солнечного излучения и в теплообменниках

©

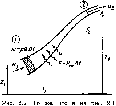
Рис. 2.3. Турбина в потоке жидкости,

но при наличии источников тепла. Теп- хами выделен контрольный объем, для ло от источника мощностью P_th пере- которого применяется закон сохране- дается трубке тока ния импульса

32