- •Возобновляемые источники энергии
- •Глава 16 посвящена очень важным для новой энергетики вопросам аккумулирования и передачи выработанной энергии.
- •Основы использования возобновляемых источников энергии
- •Введение
- •Основные понятия и определения
- •Энергии
- •Истощаемых источниках энергии
- •Научные принципы использования возобновляемых источнников энергии
- •Технические проблемы использования возобновляемых источников энергии
- •Энергии
- •Социально-экономические последствия развития энергетики на возобновляемых источниках энергии
- •Основы механики жидкости 2.1. Введение
- •Закон сохранения энергии, уравнение Бернулии
- •Закон сохранения количества движения
- •Вязкость
- •Турбулентность
- •Трение при течении в трубах
- •Глава 3.
- •Теплоперенос
- •Введение
- •Метод тепловой цепи и терминология
- •Теплопроводность
- •Конвективный теплообмен
- •Радиационный теплоперенос
- •Свойства прозрачных веществ
- •Теплоперенос посредством теплоносителя
- •Смешанный теплоперенос и его тепловая цепь
- •Глава 4 солнечное излучение 4.1. Введение
- •Космическое солнечное излучение
- •Составляющие излучения
- •Геометрия Земли и Солнца
- •Расположение приемника относительно Солнца
- •Влияние земной атмосферы
- •Оценки солнечной энергии
- •Расчет теплового баланса, общие замечания
- •Открытые нагреватели
- •Закрытые нагреватели
- •Системы с изолированным накопителем
- •Селективные поверхности
- •Вакуумированные приемники
- •Воздух)
- •Другие применения солнечной энергии
- •Введение
- •Подогреватели воздуха
- •Зерносушилки
- •Солнечные отопительные системы
- •Охлаждение воздуха
- •Опреснение воды
- •Солнечные пруды
- •Концентраторы солнечной энергии
- •Солнечные системы для получения электроэнергии
- •Глава 7
- •Фотоэлектрическая генерация
- •Введение
- •Кремниевый р—я-переход
- •Поглощение фотонов
- •Потребляемая солнечная энергия
- •Фотоэлектрические свойства цепи и нагрузки
- •Ограничения эффективности солнечных элементов
- •Конструкции солнечных элементов
- •2 При повышении температуры ширина запрещенной зоны уменьшается в таблице приведены данные для температуры окружающего воздуха
- •7.9. Фотоэмиссиоиные и термоэмиссионные системы
- •Глава 8
- •Гидроэнергетика
- •Введение
- •Основные принципы использования энергии воды
- •Оценка гидроресурсов для небольших станций
- •Активные гидротурбины
- •Реактивные гидротурбины
- •Гидроэлектростанции
- •Гидравлический таран
- •Пользуясь атласом, оцените гидроэнергетический потенциал страны или определенного района, действуя в такой последовательности.
- •Падающий на лопасти турбины Пельтона поток и отраженный образуют угол в в системе координат, связанной с лопастью. Скорость ut — тангенциаль
- •Ветроэнергетика
- •Введение
- •Классификация ветроустановок
- •Основы теории ветроэнергетических установок
- •Режимы работы ветроколеса
- •Метод линий тока
- •Характеристики ветра
- •Использование ветроколесом энергии ветра
- •Производство электроэнергии с помощью ветроэнергетических установок
- •Энергия; 6 — дорогая электроэнергия
- •Производство механической работы
- •Перспективы использования вэу
- •Фотосинтез
- •Введение
- •Трофический уровень фотосинтеза
- •Фотосинтез на уровне растений
- •Клетки губчатой ткани
- •"Замыкающая клетка устьица
- •Термодинамический анализ
- •Фотофизика
- •Фотосинтез на молекулярном уровне
- •Мембраны
- •Искусственный фотосинтез
- •Глава 11
- •Биотопливо
- •Введение
- •Классификация биотоплива
- •Сжигание биотоплива для получения тепла
- •Пиролиз (сухая перегонка)
- •Другие термохимические процессы
- •Газгольдер
- •Агрохимические способы получения топлива
- •Фермер, имеющий 50 свиней, предполагает использовать их навоз для получения биогаза в качестве топлира своего автомобиля.
- •Глава 12 энергия волн 12.1. Введение
- •Волновое движение
- •Энергия и мощность волны
- •Описание реальных волн
- •Устройства для преобразования энергии волн
- •Глава 13 энергия приливов 13.1. Введение
- •Причины возникновения приливов
- •Масштабы не соблюдены
- •Усиление приливов
- •Мощность приливных течений
- •Мощность приливного подъема воды
- •Угасающие приливы
- •Перспективные районы строительства приливных электростанций
- •Глава 14 преобразование тепловой энергии океана 14.1. Введение
- •Теплообменники
- •Требования к насосным агрегатам
- •Другие практические соображения
- •Глава 15 геотермальная энергия
- •Введение
- •Геофизика
- •Анализ свойств сухих горных пород и естественных водоносных пластов
- •Использование геотермальных ресурсов
- •Аккумулирование и передача энергии на расстояние 16.1. Значение процессов аккумулирования и передачи энергии
- •Биологическое аккумулирование
- •Химическое аккумулирование
- •Аккумулирование тепла
- •Аккумулирование электроэнергии: свинцово-кислотные батареи
- •1 Моль рь 207 г
- •Моль рьОг 239 г
- •Моля h2so4 196 г
- •Топливные элементы
- •Механическое аккумулирование
- •Передача энергии
- •Список рекомендуемой литературы
- •Оглавление
- •Глава 8. Гидроэнергетика 176
- •Глава 9. Ветроэнергетика 195
- •Глава 10. Фотосинтез 243
- •Глава 11. Биотопливо 266
- •Глава 12. Энергия волн 297
- •Глава 13. Энергия приливов 318
- •Глава 14. Преобразование тепловой энергии океана 336
- •Глава 15. Геотермальная энергия 348
- •Глава 16. Аккумулирование и передача энергии на расстояние 360
- •Твайделл Джон, Уэйр Антони Возобновляемые источники энергии
Процессы
испарения и конденсации протекают
практически при постоянной температуре,
и теплоперенос, использующий скрытую
теплоту фазового перехода, не зависит
непосредственно от температуры источника
Т\
и приемника Т2
тепла, тем не менее термическое
сопротивление такого процесса обычно
определяют так:
Тепловая
цепь, состоящая из тепловых сопротивлений.
В
§ 3.2 показано, как при анализе процессов
теплопереноса используется метод
тепловых цепей с параллльным,
последовательным и комбинированным
соединением термических сопротивлений.
В этом методе совершенно не важна
природа процесса теплопереноса
(теплопроводность, конвекция и т. д.),
стоящая за каждым термическим
сопротивлением. При построении тепловой
цепи очень важно не упустить сколько-нибудь
значительных составляющих теплового
потока и соответствующих им термических
сопротивлений. Ниже (см. гл. 5) приведено
много связанных с этим вопросом примеров.
Теплоемкость.
Электрическую
аналогию для процессов теплопереноса
можно еще более развить. Тепловая
энергия может накапливаться в различных
телах точно так же, как в электрических
цепях накапливается электрическая
энергия в конденсаторах.
Рассмотрим
для примера емкость с горячей водой,
окруженную средой с постоянной
температурой То
(рис. 3.18, а). Вода массой пг
с удельной теплоемкостью с
имеет температуру Т1,
превышающую 7V
Тепловой
поток от воды в окружающее пространство
определяется уравнением
где
знак минус означает, что Т\
уменьшается, если .величина (Т\
— То)
положительна: Ri0
—
результирующее термическое сопротивление
тепловому потоку, включающее конвекцию,
излу-
Рис.
3.18. Охлаждение горячего предмета:
физическая модель (а); модель тепловой
цепи (б); электрическая модель (в)
Rm
—
(Т\ —
T2)/rnL.
(3.51)
(3.52)
70
Смешанный теплоперенос и его тепловая цепь
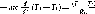
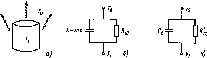
Термодинамические величины |
Электрические величины |
|||||
Величина |
Обозна |
Единицы |
Величина |
Обозна |
Единицы |
|
|
чение |
|
|
чение |
|
|
Температура |
т |
К |
Потенциал |
V |
В |
|
Поток тепла |
р |
Вт |
Ток |
I |
А |
|
Термическое сопро |
R |
К/Вт |
Сопротивление |
R |
Ом, |
|
тивление |
|
|
|
|
В/А |
|
Теплоемкость |
С |
Дж/К |
Емкость |
С |
Ф, А-с/В |
|
Задачи
Объясните
подробно, почему при последовательном
соединении термических сопротивлений
(например, на рис. 3.2, б)
/?13
= /?12-Ь/?23.
Указание:
рассмотрите, как связаны потоки тепла
в различных сопротивлениях.
Используя
определения (3.17) и (3.22), покажите, что
параметры Nu и Ra
— безразмерные величины.
Слой
жидкости заключен между двумя
горизонтальными пластинами (см. табл
3 1). Нижняя пластина с ординатой 2
= 0 имеет температуру Tj+АГ,
верхняя пластина расположена на высоте
z=d
и ее температура Т\.
Используя приведенные на рис. 3.19
измеренные профили температур,
определите толщину температурного
пограничного слоя б для представленных
на рисунке чисел Рэлея. Полагая X
= d,
определите значения чисел Нуссельта
в этих случаях. Замечание:
только в одном случае толщину
температурного пограничного слоя
71
1
z/d
Рис.
3.19. Распределение
температуры в слое жидкости- высотой
dy
ограниченном двумя плоскими
стенками с разной температурой. Числами
у кривых обозначено отношение Ra/Ra„
где Ra, = 1700, ниже
которого конвекция отсутствует
О (Г-Т,)/АТ '
(3.13)
можно определить непосредственно, а
именно, она равна просто высоте слоя
жидкости в окрестности пластины, если
температура в этом слое линейно зависит
от высоты.
Рассчитайте
излучательные потери тепла в течение
1 ч кастрюлей из примера 3.3 и покажите,
что они действительно меньше конвективных
потерь тепла.
Сформулированный
Ньютоном закон охлаждения гласит, что
скорость охлаждения тела пропорциональна
разности температур тела и окружающей
среды, т. е. скорость охлаждения не
зависит от других факторов, например
от /ветра. Рассчитайте конвективные
потери тепла плоской пластиной площадью
1 м2 с температурой 50° С в воздух
с температурой 20° С при скорости ветра:
а) 0
м/с, б) 5 м/с, в) 10 м/с
Рассчитайте
тепловой поток от пластины задачи 3.5
при тех же скоростях ветра, суммируя
тепловые потоки при вынужденной и
свободной конвекции.
Потери
тепла через окна.
В
комнате два окна высотой 1,5 м и шириной
0,8 м со стеклами толщиной
мм
(рис. 3.20). Температура в комнате 20° С,
температура наружного воз-
Сгпекло
Теплый
комнатный
]
воздух
Наружный
воздух
Температурные
пограничные слои
'12
К
i
5)
-о
72
Рис.
3.20. Теплопередача через окно (см. задачу
3.7)