
- •Возобновляемые источники энергии
- •Глава 16 посвящена очень важным для новой энергетики вопросам аккумулирования и передачи выработанной энергии.
- •Основы использования возобновляемых источников энергии
- •Введение
- •Основные понятия и определения
- •Энергии
- •Истощаемых источниках энергии
- •Научные принципы использования возобновляемых источнников энергии
- •Технические проблемы использования возобновляемых источников энергии
- •Энергии
- •Социально-экономические последствия развития энергетики на возобновляемых источниках энергии
- •Основы механики жидкости 2.1. Введение
- •Закон сохранения энергии, уравнение Бернулии
- •Закон сохранения количества движения
- •Вязкость
- •Турбулентность
- •Трение при течении в трубах
- •Глава 3.
- •Теплоперенос
- •Введение
- •Метод тепловой цепи и терминология
- •Теплопроводность
- •Конвективный теплообмен
- •Радиационный теплоперенос
- •Свойства прозрачных веществ
- •Теплоперенос посредством теплоносителя
- •Смешанный теплоперенос и его тепловая цепь
- •Глава 4 солнечное излучение 4.1. Введение
- •Космическое солнечное излучение
- •Составляющие излучения
- •Геометрия Земли и Солнца
- •Расположение приемника относительно Солнца
- •Влияние земной атмосферы
- •Оценки солнечной энергии
- •Расчет теплового баланса, общие замечания
- •Открытые нагреватели
- •Закрытые нагреватели
- •Системы с изолированным накопителем
- •Селективные поверхности
- •Вакуумированные приемники
- •Воздух)
- •Другие применения солнечной энергии
- •Введение
- •Подогреватели воздуха
- •Зерносушилки
- •Солнечные отопительные системы
- •Охлаждение воздуха
- •Опреснение воды
- •Солнечные пруды
- •Концентраторы солнечной энергии
- •Солнечные системы для получения электроэнергии
- •Глава 7
- •Фотоэлектрическая генерация
- •Введение
- •Кремниевый р—я-переход
- •Поглощение фотонов
- •Потребляемая солнечная энергия
- •Фотоэлектрические свойства цепи и нагрузки
- •Ограничения эффективности солнечных элементов
- •Конструкции солнечных элементов
- •2 При повышении температуры ширина запрещенной зоны уменьшается в таблице приведены данные для температуры окружающего воздуха
- •7.9. Фотоэмиссиоиные и термоэмиссионные системы
- •Глава 8
- •Гидроэнергетика
- •Введение
- •Основные принципы использования энергии воды
- •Оценка гидроресурсов для небольших станций
- •Активные гидротурбины
- •Реактивные гидротурбины
- •Гидроэлектростанции
- •Гидравлический таран
- •Пользуясь атласом, оцените гидроэнергетический потенциал страны или определенного района, действуя в такой последовательности.
- •Падающий на лопасти турбины Пельтона поток и отраженный образуют угол в в системе координат, связанной с лопастью. Скорость ut — тангенциаль
- •Ветроэнергетика
- •Введение
- •Классификация ветроустановок
- •Основы теории ветроэнергетических установок
- •Режимы работы ветроколеса
- •Метод линий тока
- •Характеристики ветра
- •Использование ветроколесом энергии ветра
- •Производство электроэнергии с помощью ветроэнергетических установок
- •Энергия; 6 — дорогая электроэнергия
- •Производство механической работы
- •Перспективы использования вэу
- •Фотосинтез
- •Введение
- •Трофический уровень фотосинтеза
- •Фотосинтез на уровне растений
- •Клетки губчатой ткани
- •"Замыкающая клетка устьица
- •Термодинамический анализ
- •Фотофизика
- •Фотосинтез на молекулярном уровне
- •Мембраны
- •Искусственный фотосинтез
- •Глава 11
- •Биотопливо
- •Введение
- •Классификация биотоплива
- •Сжигание биотоплива для получения тепла
- •Пиролиз (сухая перегонка)
- •Другие термохимические процессы
- •Газгольдер
- •Агрохимические способы получения топлива
- •Фермер, имеющий 50 свиней, предполагает использовать их навоз для получения биогаза в качестве топлира своего автомобиля.
- •Глава 12 энергия волн 12.1. Введение
- •Волновое движение
- •Энергия и мощность волны
- •Описание реальных волн
- •Устройства для преобразования энергии волн
- •Глава 13 энергия приливов 13.1. Введение
- •Причины возникновения приливов
- •Масштабы не соблюдены
- •Усиление приливов
- •Мощность приливных течений
- •Мощность приливного подъема воды
- •Угасающие приливы
- •Перспективные районы строительства приливных электростанций
- •Глава 14 преобразование тепловой энергии океана 14.1. Введение
- •Теплообменники
- •Требования к насосным агрегатам
- •Другие практические соображения
- •Глава 15 геотермальная энергия
- •Введение
- •Геофизика
- •Анализ свойств сухих горных пород и естественных водоносных пластов
- •Использование геотермальных ресурсов
- •Аккумулирование и передача энергии на расстояние 16.1. Значение процессов аккумулирования и передачи энергии
- •Биологическое аккумулирование
- •Химическое аккумулирование
- •Аккумулирование тепла
- •Аккумулирование электроэнергии: свинцово-кислотные батареи
- •1 Моль рь 207 г
- •Моль рьОг 239 г
- •Моля h2so4 196 г
- •Топливные элементы
- •Механическое аккумулирование
- •Передача энергии
- •Список рекомендуемой литературы
- •Оглавление
- •Глава 8. Гидроэнергетика 176
- •Глава 9. Ветроэнергетика 195
- •Глава 10. Фотосинтез 243
- •Глава 11. Биотопливо 266
- •Глава 12. Энергия волн 297
- •Глава 13. Энергия приливов 318
- •Глава 14. Преобразование тепловой энергии океана 336
- •Глава 15. Геотермальная энергия 348
- •Глава 16. Аккумулирование и передача энергии на расстояние 360
- •Твайделл Джон, Уэйр Антони Возобновляемые источники энергии
для
органических веществ, например древесины;
б) пары жидкости из влажной атмосферы
диффундируют внутрь пористого материала
и там конденсируются (см. § 3.7.).
Еще
одним свойством физических тел,
непосредственно связанным с их
теплопроводностью, является
температуропроводность,
характеризующая процесс изменения
температуры в различных точках тела
в процессе кондуктивного переноса
тепла. Количественно температуропроводность
характеризуется коэффициентом
температуропроводности, равным
а
= к/рсу
где
р —плотность, а с
— удельная теплоемкость при постоянном
давлении, а
имеет размерность м2/с, как и
коэффициент кинематической вязкости
v [см. (2.9)].
Из
(3.12) следует, что температура тела будет
изменяться тем быстрее, чем выше его
теплопроводность [велик коэффициент
теплопроводности К
в числителе (3.12)] и чем меньше тепла
расходуется на его нагрев (мала
удельная объемная теплоемкость в
знаменателе).
Характерное
время «диффузии» температуры в среде
на расстоянии у
в процессе теплопроводности — порядка
у1
/а.
Теплообмен
при свободной и вынужденной конвекции.
Конвективный
теплообмен
— это процесс передачи тепла жидкости
или телу при их движении относительно
друг друга. Так как движение есть
перемещение * макроскопических объемов
жидкости, естественно, что при этом
происходит и перенос тепла. Как правило,
конвективный перенос тепла происходит
гораздо эффективнее, чем кондуктивный
перенос в неподвижной жидкости.
При
свободной конвекции (называемой также
естественной) движение жидкости
возникает вследствие разности температур
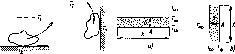
в различных ее частях. Рассмотрим
частицу жидкости, соприкасающуюся
с горячей поверхностью (рис. 3.3). В
начальный мо-
Рис.
3.3. Движение жидкости около горячей
поверхности при свободной конвекции
(r2>7'i)
Рис.
3.4. Температурный пограничный слой при
свободной конвекции около горизонтальной
(а)
и вертикальной (б)
горячих поверхностей
47 (3.12)
Конвективный теплообмен
мент
эта частица поглощает тепло от поверхности
вследствие теплопроводности, расширяется
при нагревании и ее плотность уменьшается.
Вследствие этого она поднимается вверх,
в область более низких температур,
осуществляя таким образом перенос
тепла в направлении уменьшения
температуры жидкости.
При
вынужденной конвекции жидкость
перемещается под действием внешних
сил, например насоса или ветра. Это
движение не зависит от распределения
температуры в жидкости. Очевидно,
что существуют и промежуточные случаи
конвекции — частично свободной и
частично вынужденной.
Число
Нуссельта. При
рассмотрении конвективного теплообмена
обычно используют упрощенную модель
этого процесса. Предполагают, что
жидкость около рассматриваемой
поверхности неподвижна. Затем
рассматривают перенос тепла поперек
прилегающего к поверхности неподвижного
пограничного слоя толщиной б и площадью
основания А.
Полагают, что температура на
прилегающей к поверхности границе слоя
равна температуре поверхности TWy
на внешней поверхности слоя равна
температуре жидкости вне его. В такой
модели теплопроводностный перенос
тепла поперек температурного пограничного
слоя определяется выражением
р
^ (тw
тоо) t
Ч=и
=
—ъ—- (злз)
где
к—
коэффициент теплопроводности жидкости.
В
этой модели толщина пограничного слоя
б —условная величина, ее нельзя
измерить. Однако в каждом конкретном
случае можно ввести величину X
—
некий характерный размер рассматриваемой
задачи (рис. 3.4). Из (3.13) следует
_
р
_k(Tw-TQO)_
х k(Tw-T„)^mk(Tw-T00)
4
А 6 6 X
Здесь
Nu—число Нуссельта для
данного конкретного случая. Число
Нуссельта — безразмерный параметр
подобия процессов конвективного
теплообмена, зависящий от геометрии
тела и картины течения в его
окрестности.
Сравнивая
результаты § 3.2 и (3.14), получаем следующие
зависимости:
конвективное
термическое сопротивление
Rv
= X/NukA;
конвективное
удельное термическое сопротивление
rv
= RvA=X/Nu\;
коэффициент
теплоотдачи или теплопередачи
hv=l/r0
= NuX/X.
48
(3
14) (3.15) (3.16) (3.17)
Рис.
3.5. Обтекание горячей пластины. Сплошными
линиями показаны траектории частиц
жидкости в области А,
достаточно удаленной от поверхности
пластины в ламинарной области В
в окрестности передней кромки пластины
и в турбулентной области С
Интенсивность
конвективного теплопереноса определяется
следующими факторами: свойствами
жидкости, скоростью течения жидкости,
формой и размером поверхности.
Число
Нуссельта является безразмерной
величиной измерения тепла при конвективном
теплообмене .и поэтому зависит только
от безразмерных характеристик
перечисленных выше факторов. Определяя
эти характеристики, следует разделять
случаи вынужденной и свободной
конвекции.
Вынужденная
конвекция. При
заданной форме поверхности безразмерным
масштабом скорости является число
Рейнольдса
R
e
= uX/v. (3.18)
В
§ 2.5 показано, что число Рейнольдса
определяет картину течения, в частности,
будет ли течение ламинарным или
турбулентным. При обтекании плоской
пластины (рис. 3.5) при Re^
^3-105 устанавливается турбулентный
режим течения, при этом возрастает
теплоотдача, вызванная поперечными
потоку турбулентными пульсациями
скорости. Поток тепла, передаваемого
телом потоку жидкости или наоборот,
зависит от коэффициента температуропроводности
а
жидкости, а также от коэффициента
кинематической вязкости v
(который можно считать количественной
характеристикой скорости переноса
импульса), так как от него зависит
число Рейнольдса, определяющее характер
течения. Таким образом, число Нуссельта
при вынужденной конвекции зависит
только от двух параметров, так как
переменные А,, р и с
объединены
параметром а
(3.12). Эти два параметра v
и а
определяют безразмерную переменную,
называемую числом
Прандтля
Pr
— v/a.
Если
число Прандтля велико, изменения в
пространственном распределении скорости
(или количества движения) жидкости
будут гораздо более резкими, чем
изменения в распределении температуры.
Для большинства жидкостей число Прандтля
Рг~1.
49
(3.19)
Форма тел и их расположение |
Режим |
Формулы для расчета чисел Нуссельта |
Горизонтальная |
Ламинарный |
Nu=0,54Ra0;25 |
плоская пластина |
(102< Ra < 10s) |
Nu = 0,14RaOM |
(Я —диаметр или полусумма |
Турбулентный |
|
сторон пластины) |
(Ra> 105) |
Nu=0,47Ra°'25 |
Горизонтальный цилиндр |
Ламинарный |
|
(X — диаметр цилиндра) |
< 104 < Ra < 109) |
Nu=0,10Ra°-33 |
|
Турбулентный |
|
|
(Ra> 109) |
Nu=0,56Ra°'25 |
Вертикальная плоская пластина |
Ламинарный |
|
или вертикальный цилиндр |
(104<Ra<109) |
Nu=0,20Ra°'4° |
(Я —высота пластины или ци |
Турбулентный |
|
линдра) |
(10э < Ra < 1012) |
Nu=0,062Ra°'33 |
Параллельные пластины |
Турбулентный |
|
(наклон не более 50°) (X —рас |
(Ra> 105) |
|
стояние между пластинами) |
|
|
50
Форма тел и их расположение |
Режим |
Формулы для расчета |
Плоская пластина (X — размер пластины по потоку) |
Ламинарный (Re<5-105) Турбулентны г (Re> 5-105) |
Nu = 0,664Re05Pr0,33 Nu = 0,37Re0,8Pr°33 |
Круговой цилиндр, поперечное обтекание [X — диаметр цилиндра) |
Ламинарный (0,1 < Re < 1000) Турбулентный (103<Re<5* 104) |
Nu =(0,35 + 0,56Re0,52) Pr03 Nu = 0,26Re0,6Pr0,3 |
Теплообмен внутри круглой трубы (X — внутренний диаметр трубы D, L — длина трубы) |
Ламинарный, короткая труба (Re<2300, G.> 10) Турбулентный (Re> 2300) |
Gi = RePr (D/L)~4Q/anL Nu = 1,86G?’33 Nu = 0,027Re0,8Pr0,33 |
Плоская пластина в воздухе (сложный теплообмен) |
Х>0,1 м иС20 м/с |
h—a-\-bu a = 5,7 Bt-m_2«K-1 6 = 3,8 (Вт* m-VK-')/ (m*c-1) |
Общий случай |
— |
NUj =ГПаХ (NUBbjMy*ui> NUcbo6) N U 1 <C N UoAHOBp Nивынужд‘"|~ NUCBo6 |
gfiAT
Рис.
3.6. Схема движения частицы жидкости при
свободной конвекции. Стрелками
обозначены Архимедова сила (вверх),
сила трения (вниз), тепловой поток
от
частицы (в стороны)
ем
архимедовой силы, пропорциональной
произведению gPA7\ испытывая
сопротивление сил вязкости, пропорциональных
v. При этом температура
жидкости (а следовательно, и подъемная
архимедова сила) уменьшается со
скоростью, пропорциональной
коэффициенту температуропроводности
а.
Следовательно, интенсивность конвективного
теплообмена пропорциональна g$AT/avt
т. е. числу Рэлея Ra. Параметр
Xs
введен для того, чтобы обезразмерить
это отношение. Экспериментально
обнаружено, что при Ra^lO3
свободная конвекция практически
отсутствует, а при Ra^lO5
имеет турбулентный характер. Из
изложенного следует, что число Нуссельта
при свободной конвекции зависит в
основном от числа Рэлея и в какой-то
степени от числа Прандтля, так как это
диктуется условием безразмерное™
числа Нуссельта. Формулы для расчета
чисел Нуссельта в некоторых случаях
приведены в табл. 3.1 и 3.2. Точность этих
формул — не выше 10%. В некоторых работах
в этих формулах используется число
Грасгофа Gr = Ra/Pr.
Так как оно физически менее наглядно,
мы его не используем. Отметим, что число
Нуссельта (а следовательно, и термическое
сопротивление) при свободной конвекции
неявно зависит от перепада температур
АТ
через число Рэлея, в которое он входит.
Это совершенно понятно, так как при
большем температурном перепаде
конвективное движение интенсивнее, а
значит, интенсивнее и теплоперенос.
При вынужденной же конвекции число
Нуссельта и термическое сопротивление
практически не зависят от перепада
температур АТ.
Расчет
конвективного теплообмена. Из-за
сложности в общем случае картины течения
жидкости чисто теоретических методов
52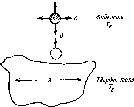
расчета
конвективного теплообмена не существует.
Во всех расчетах так или иначе используются
результаты экспериментальных
исследований. Представление этих
результатов в безразмерном виде
позволяет переносить их на подобные
тела других размеров.
Стандартный
алгоритм расчета конвективного
теплообмена состоит в следующем:
Составляется
схема рассматриваемого объекта.
Схема
объекта расчленяется на стандартные
элементы.
Для
каждого из этих элементов:
а) определяются
характерные размеры (X);
б) рассчитываются
числа Рейнольдса Re и/или
числа Рэлея Ra;
в) из
таблиц выбираются соответствующие
полученным значениям Re
или Ra формулы для расчета
числа Нуссельта Nu (для
ламинарного и турбулентного режимов
течения эти формулы обычно различны);
г) рассчитываются
числа Нуссельта, а следовательно, и
потоки тепла P
= qA.
Суммируются
тепловые потоки от всех элементов, т.
е. определяется полный поток тепла от
рассматриваемого объекта.
Если
в справочных данных используется число
Gr, то следует учесть, что
Ra = GrPr.
Пример
3.2. Свободная конвекция между параллельными
пластинами. Две
плоские пластины размером 1X1
м2
разделены слоем воздуха толщиной 3 см.
Температура нижней пластины 70° С,
верхней 45° С. Для исключения концевых
эффектов пластины по краям скреплены
друг с другом теплоизоляционным
материалом. Рассчитайте конвективное
термическое сопротивление этой системы
и тепловой поток от одной пластины к
другой.
Решение.
На рис. 3.7, а
представлен стандартный элемент — две
плоские параллельные пластины. Наличие
теплоизоляции по краям пластин позволяет
считать, что теплоперенос осуществляется
только в результате свободной конвекции.
Используя (3.22), при среднем значении
температуры 57° С (330 К)
Рис.
3.7. Примеры расчетных схем для конвективного
теплопереноса: параллельные пластины,
пример 3.2 (а), и кастрюля, пример 3.3 (б)
53
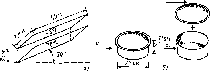
определяем
число Рэлея (для воздуха при 7’ = 57°С, а
= 2,6»10 5 м2*с ',
Ка=1ЁШ^ГЛГ: (9,8
м-с~
)
(1/330 К)
3(25 К) =
av
av (2,6-10“ м -с
)(1,8-10 м2-с-1)
=4,1-104.
Соответствующее
значение числа Nu для
этого случая, учитывая, что Ra
незначительно меньше 105, определяем
по формуле (см. табл. 3.1)
Nu
=0,062Rao,33=2,06.
Из
(3.16) находим
X 0,03
м Л рл it 2
/п
/•„
= = =0,52 К м /Вт.
Nu*.
(2,06)(0,028 м-'-К”1)
Тепловой
поток определяем по (3.5):
Ш
(1
м2)
г°
~ 0,52
К-м2-Вт
р=АЬТ=
(1
м2)
(25 К)
=48 ^
Следует
отметить, что:
параметр
g$/av
(равный Ra/X3AТ)
обычно затабулирован;
параметры
газа оцениваются по его средней
температуре (в рассматриваемом
случае можно положить ее равной средней
температуре пластин);
при
расчете всех безразмерных параметров
надо пользоваться одной системой
единиц измерения (например, СИ).
Пример
3.3. Конвективное охлаждение кастрюли.
На плите находится металлическая
кастрюля с водой, размеры которой
приведены на рис. 3.7, б.
Наружная
поверхность кастрюли светлая и блестящая.
Какое минимальное количество энергии
необходимо, чтобы поддерживать кипение
в кастрюле в течение 1 ч: 1) при
отсутствии ветра и 2) при легком ветре
со скоростью 3 м/с?
Решение.
Считаем, что кастрюля плотно закрыта
крышкой, поэтому нет потерь тепла на
испарение. Как показано ниже, в задаче
3.4, для заданной поверхности кастрюли
можно пренебречь радиационными потерями
тепла. Так как теплопроводность стенок
кастрюли велика, задача сводится к
вычислению конвективных потерь
тепла с верхней и боковой поверхностей
цилиндра с температурой 100° С. Считать,
что температура окружающего воздуха
равна 20° С, а значение его средней
температуры 7\ необходимое для • расчета
тепл оперен оса, равно 60° С.
Только
свободная конвекция.
Для верхней поверхости цилиндра
(крышки) имеем (3.22)
Ra=(5,8-107
м~3-К-1) (0,22 м)3(80
К)=4,9-107, тогда (см. табл. 3.1)
Nu=0,14
Ra0,33 = 48,4,
откуда
Якр
= у4ШиДГ/Аг = (я/4)(0,22 м)2(0,027
Вт-м'^К-1) (48,4) (80
К)/(0,22 м) =
=
18 Вт.
54
Для
боковой поверхности цилиндра ЛГ = 0,11
ми
Ra6„,
= RaKp(0,11
м/0,22м)3=6,1
• 106,
Nu=0,56
Ra°25=27,8,
откуда
Рбок
= л(0,22 м) (0,11 м) (0,027 Вт-м"1
-К_1)(27,8) (80 К)/(0,11 м)=41 Вт. Окончательно
имеем
/^своб
= Ркр
+ Рбок
= 59 Вт.
Отсюда
искомая энергия равна потерям тепла
полученной интенсивности в течение 1
ч, т. е.
(0,059
кВт) (3600 с) =0,21 МДж
Совместное
действие свободной и вынужденной
конвекции.
В эом случае рассчитываем потери тепла
при вынужденной конвекции, складываем
их с уже известными потерями при
свободной конвекции и получаем в
результате потери тепла при данном
конвективном теплопереносе.
Для
крышки имеем
Re=(3
м-с_|) (0,22 м)/(1,9-10“5
м2-с~')
= 3,5-104,
откуда
(см. табл. 3.2)
Nu
=0,664Re°’5Pr<U3=
110 (ламинарный режим Re<5*105)
и
PKp=AXNuAT/Х
= 42
Вт.
Для
боковой поверхности, как и для крышки,
Re
= 3,5-104
и
Nu
=0,26 Re06
Рг0,3
= 124,
Р6ж
= л(0,22
м) (0,11 м) (0,027 Вт-м-'-К".1) (124) (80
К)/(0,22 м) =93 Вт. Отсюда
Рвынужд=93
+ 42=135 Вт и полные конвективные потери
тепла равны
/^Рвынужд
+ ^своб^ 194 Вт = 0,7 МДж/ч.
Суммарная
погрешность этих расчетов может
достигать 50% и более, хотя погрешность
отдельных формул существенно меньше.
Это объясняется тем, что в случае, когда
свободная и вынужденная конвекции
одного порядка, полный тепловой поток
не будет в общем случае равен сумме
рассчитанных независима друг от
друга тепловых потоков при свободной
и вынужденной конвекциях, так как,
например, направление движения газа
при свободной конвекции может быть
противоположным
55
