коэффициенту диффузии (см. определение коэффициента термо­диффузии х в § 3.3). Это означает, что, например, характерное время диффузионного переноса количества движения на рас­стояние х равно x²/v.

2. Турбулентность

Турбулентное движение жидкости является следствием не­устойчивости быстрых течений. Рассмотрим ламинарное течение в трубе, характеризующееся прямолинейными траекториями частиц жидкости (рис. 2.5, а), в которое эпизодически вносятся возмущения (например, постукиванием по трубе). Траектории частиц жидкости при этом будут хаотически искривляться и, если частицы движутся достаточно быстро, силы трения в жид­кости будут не в состоянии вернуть им первоначальный прямо­линейный характер. Более того, в определенных условиях возму­щенные частицы будут искривлять траектории все большего числа соседних частиц, и в результате движение всех частиц становится хаотическим или турбулентным (рис. 2.5, б). Харак­тер движения частиц жидкости, т. е. будет ли течение ламинар­ным или турбулентным, определяется отношением инерционных сил (пропорциональных количеству движения) к вязким силам. Это отношение называется числом Рейнольдса:

R е = иХ/у, (2.10)

где и — среднее значение скорости течения; X — характерный размер течения (в рассматриваемом случае это диаметр трубы); v — кинематическая вязкость. Экспериментальные исследования показали, что течение в трубах становится турбулентным при Re>2300.

В турбулентных течениях на среднюю скорость потока накла­дываются более или менее случайные пульсации скорости. Этй пульсации скорости имеют трехмерный характер и не влияют на среднюю скорость потока. Таким образом, жидкая частица, двигаясь вдоль трубы, совершает в то же время быстрые попе­речные перемещения, как это показано на рис. 2.5, б. Так как жидкость не проскальзывает вдоль поверхности трубы (см. § 2.4),

шш»

ШШШ а) ШЯШШШ S)

Рис. 2.5. Траектории жидкости при ламинарном (а) и турбулентном (б) режимах

течения

35

среднее значение скорости у поверхности мало, а в центре трубы велико. Вследствие поперечных пульсаций скорости частицы жидкости с большой продольной скоростью перемещаются к стенке трубы, а с малой скоростью — в центр трубы. При этом процесс переноса количества движения в поперечном направле­нии оказывается гораздо более эффективным, чем при молеку­лярном переносе, описанном в § 2.4, так как длина свободного пробега молекул—порядка нанометров, а длина турбулентных пульсаций может быть порядка радиуса трубы. При турбулент­ном переносе импульса силы трения, препятствующие продоль­ному движению жидкости, резко возрастают.

Если температура стенок трубы выше температуры жидкости, поперечные пульсации скорости обеспечивают перенос тепла от стенок внутрь трубы. При этом по той же причине, что и при передаче импульса, перенос тепла оказывается более интенсив­ным, чем при молекулярном переносе. Более детально этот меха­низм теплопроводности рассмотрен в § 3.4.

2. Трение при течении в трубах

Рассмотрим течение жидкости в трубе длиной L и с постоян­ным диаметром D. Какой перепад давлений Ар между входным и выходным концами трубы надо создать, чтобы при наличии трения в трубе средняя скорость жидкости в ней была равна и?

Очевидно, Ар — это работа, совершаемая против сил трения при перемещении единицы массы жидкости на длину L. Если считать, что в любом сечении трубы картина течения будет одинаковой, то работа против сил трения пропорциональна длине и Ар возрастает с увеличением L. Так как основной вклад в сопротивление создают стенки трубы (из-за условия прилипания, см. § 2.4), то очевидно, что удаление стенок трубы от высоко­скоростного потока в ее центре, т. е. увеличение диаметра трубы, уменьшает ее сопротивление. Из (2.8) следует, что сила трения возрастает с увеличением скорости потока, поэтому и Ар воз­растает с и. Из уравнения Бернулли (2.3) видно, что величина (1 /2) р и² имеет ту же размерность, что и А р. Все эти зависимости можно объединить единственным уравнением

Ар = 2£ (L/D) (ри²), (2.11)

в котором £ — безразмерный коэффициент сопротивления трубы, зависящий от условий эксперимента, точнее, от геометрии тече­ния, т. е. от формы линий тока.

Величина ри² в (2.11) имеет ту же размерность, что и пере­пад давлений Ар, поэтому коэффициент £ показывает, чему равна работа сил давления по преодолению сопротивления трубы (Ар) в сравнении с кинетической энергией потока единичного

36

	ОМ -
fit	0,0175 ~
1	0,015 \
1	0,0125 ~
I	0,01 ~
§* 0,0075 ~
<о
1	0,005 ~
	0.0025
	10

Рис. 2.6. Коэффициент сопротивления труб £ [см. (2.11)]. Штриховая кривая соответствует ламинарному течению

37

Материал трубы	Шероховатость мм
Поливинилхлорид	0 (гладкая)
Асбестоцемент	0,012
Сталь (новая)	0,1
Бетон (гладкий)	0,4.

Следовательно, режим течения турбулентный. Для бетона (согласно табл. 2.1) £ = 0,4 мм, параметр шероховатости

_l/0=^L₌₀,ooi3.

300 мм

Для данных значений Re и 1/D из рис. 2.6 определяем £ = 0,0050.

Представим (2.11) через потери напора на трение:

H, = Ap/pg=2iLu²/Dg. (2.12)

Отсюда

н (2)(5,0-10-³)(200м)(1,4 м-с-')² , _{g м} ' (0,3 м) (9,8 м-с"²)

Следует напомнить, что при подобных расчетах все величины следует брать в одной системе единиц, например в СИ.

На рис. 2.6 показана только одна кривая при Re<2000, откуда следует, что коэффициент сопротивления £ в этом диапа­зоне не зависит от шероховатости трубы J*. Это объясняется тем, что в ламинарном течении шероховатость не в состоянии нару­шить его устойчивость. В таком течении потери давления Ар определяются с использованием (2.8) для вязких напряжений, как показано в задаче 2.4. Соответствующее выражение для коэффициента сопротивления имеет вид

£=16 v/(uD). (2.13)

Задачи

1. На рис. 2.7, а показан идеальный расходомер (трубка) Вентури для измерения расхода жидкости в трубах.

38

Рис. 2.7. К задаче 2.1. Расходомеры Вентури с плавным сужением канала (а)

и шайбой (б)

а) Используя уравнения сохранения массы и энергии, покажите, что объем­ный расход жидкости через поперечное сечение 1 равен

б) Чему равен объемный расход через поперечное сечение 2 (рис. 2.7, а)?

в) Давления р\ и р₂ измеряются высотой столбов жидкости в отводных трубках, как показано на рис. 2.7, а. Покажите на рисунке величину, соответ­ствующую члену в квадратных скобках в выражении из задачи 2.1(a).

г) На рис. 2.7, б показано устройство для измерения параметров потока в трубе постоянного поперечного сечения. Оно состоит из шайбы с отверстием, имеющим острые кромки, помещенной в трубу, и двух отводов для измерения давления до и после шайбы. Можно ли разность этих давлений использовать в формуле задачи 2.1(a) для определения расхода жидкости в трубке или резуль­тат будет завышен (занижен) и почему?

Указание: используйте уравнение для полной энергии (2.1).

2. 2. Из двумерного сопла истекает горизонтально прямоугольная в сечении струя шириной 6, высотой Л. Струя натекает на бесконечную плоскую наклон­ную преграду, как показано на рис. 2.8.

а) Пренебрегая эффектами вязкости и гравитации, покажите, используя уравнение Бернулли, что u\=u2 = uj.

Указание: изменением давления поперек тонкого слоя можно пренебречь.

б) Чему равна составляющая действующей на жидкость силы, параллель­ная преграде? Рассматривая изменение количества движения жидкости в рацио-

<Э = _и,Л,=Л, [(Л,/Л₂)²-1]-^|/2{2£р1^+(₂,-_г2)]}^1/2

Рис. 2.8. К задаче Натекание плоской ст на наклонную прегр

39

нально выбранном контрольном объеме и используя уравнение сохранения массы, покажите, что расход жидкости вверх и вниз по преграде соответственно равен

в) Получите выражение для действующей на преграду силы и определите ее величину при 6 = 10 см, h~ 1 см, Q = 10 л/с, а = 60°.

3. Рассмотрите установившееся ламинарное течение жидкости между двумя неподвижными пластинами с ординатами у=0 и y — D (см. рис. 2.4). Жидкость движется вправо (в сторону увеличения координаты х) под действием постоянно­го градиента давления др/дх <0.

а) Чему равны силы, действующие на элемент жидкости длиной Л*, шириной Л2 и высотой от у до у-\-&у? Покажите, что в таком течении действующие на эле­мент жидкости силы связаны соотношением

б) Интегрируя это соотношение, покажите, что скорость течения на высоте у равна

в) Пластины имеют ширину 5>D, так что концевыми эффектами можно пре­небречь. Покажите, что в этом случае объемный расход жидкости между пластина­ми равен

3. Ламинарное течение в трубе. Рассмотрим направленное вертикально вниз течение жидкости в цилиндрической трубе диаметром D — 2R и с постоянным градиентом давления. Пусть х — расстояние вдоль трубы, г —расстояние от ее оси.

а) Как и в задаче 2.3, покажите, что силы, действующие на кольцевой эле­мент жидкости длиной Ах и радиусами г и г + Аг, связаны соотношением

Указание: сила трения, действующая на кольцевую поверхность радиусом г, равна (2лглг) т (г), а г изменяется поперек трубы.

б) Интегрируя соотношение пункта а), покажите, что скорость течения свя­зана с радиусом г соотношением

Q,=y (I +cos a) Q_h <?2 = у(1—cosa)Q/.

д / ди\

Ty^w)

др_

дх

в) Покажите, что объемный расход жидкости в трубе равен

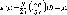
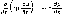
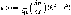
г) Среднее значение скорости потока в трубе равно u=Q/A. Используя это равенство, выражение для Q из пункта в) и (2.11), покажите, что м£ = = 16v/D, т. е. получите (2.13).

3. Оценивая результаты примера 2.1, можно подумать, что в этом случае было бы дешевле использовать трубы из поливинилхлорида значительно меньше­го диаметра.

а) Опровергните это предположение, рассчитав потери напора на трение при течении воды в ПХВ-трубе диаметром 5 см, длиной 200 м и расходе 0,1 м³/с, по­казав, что эти потери чрезмерно высоки.

б) Определите предельную скорость воды в такой трубе, если течение в ней происходит только под действием силы тяжести.

Указание: положите Hf — L (вертикальная труба), оцените £ и определите скорость и.

3. Объемный расход жидкости через стальную трубу диаметром Д дли­ной L равен Q. Полагая коэффициент трения трубы £ слабо зависящим от числа Рейнольдса, покажите, что потери напора на трение пропорциональны D^-5 (при фиксированных L и D).

Решения и ответы

1. а) Из уравнения сохранения массы U2 = U\A\/A₂. Используйте уравнение Бернулли в форме (2.2).

б) Q.

в) Геометрическая разность уровней жидкости в отводах.

г) Рассчитанный расход будет завышен, так как в расчетах не учитываются потери кинетической энергии потока при его турбулизации перед и за шайбой.

2. а) В (2.4.) положите р\=р₂ и g — 0.

б) Нулю, так как жидкость невязкая. Из уравнения сохранения массы сле­дует Aj=A\-\-A₂. Используйте уравнение сохранения количества движения в про­екции на плоскость преграды:

pAjuJcos а = рА\и² — рА₂и₂.

в) F = pQjUj sina = 86 Н, направлена перпендикулярно преграде (вниз вправо).

3. а) Разность сил давления в сечениях х и х + Ах и разность сил трения, действующих на высоте у-\-Ау и у. Используйте (2.8).

б) и — 0 при у — 0, y — D.

в) £t = \u(Bdy).

4. а) \(др/дх)Ах\[л(г-{-Аг)² — лг²] = т(г)2лгАх — т(г-{-Аг)2л(г-\-Аг)Ах.

б) Из условия симметрии ди/дг — 0 при г = 0, а также и = 0 при r~R.

в) Q — ^u-2nrdr.

5. а) См. пример 2.1. В результате получаем Hf— 12 km^L.

б) £ = 0,006 (слабая зависимость от Re в этом диапазоне), при этом и — = 4,4 м/с, Q = 8 л/с.

6. Учтите, что u = Q J(^-лй²^.

41