5.6. Распределения, связанные с нормальным распределением (распределения Пирсона, Стьюдента, Фишера - Снедекора)
Нормальный закон распределения случайной величины - наиболее часто встречающийся закон, он играет большую роль в теории вероятностей. Нормальный закон распределения является предельным законом, к которому приближаются другие законы распределения. Однако на практике встречаются и другие законы, связанные с нормальным. Они представляют собой распределения некоторых функций от нормально распределенной величины. Рассмотрим такие распределения.
Распределение Пирсона (распределение )
Пусть
- независимые случайные величины, имеющие
нормированное нормальное распределение,
,
.
Величина
,
равная сумме квадратов случайных величин
,
то есть
,
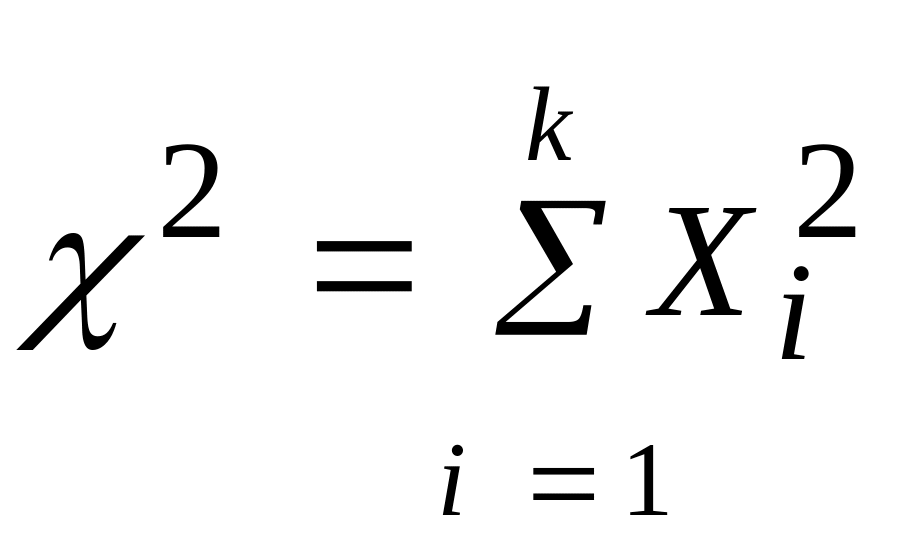также будет случайной величиной. Она
имеет распределение Пирсона1
или распределение
(хи-квадрат) с k
степенями свободы.
Из
определения следует, что случайная
величина
может
принимать только неотрицательные
значения. Число степеней свободы k
распределения
является параметром этого распределения,
поэтому часто распределение Пирсона с
k
степенями
свободы обозначают
.
Функция плотности вероятности распределения с k степенями свободы имеет вид
где
- гамма-функция Эйлера; для целых
положительных значений
.
Примечание. Более подробные сведения о гамма-функции и ее свойствах можно узнать из полных курсов интегрального исчисления.
Графики
функции плотности вероятности
распределения
с различными степенями свободы изображены
на рис. 24 и 25, где
;
;
.
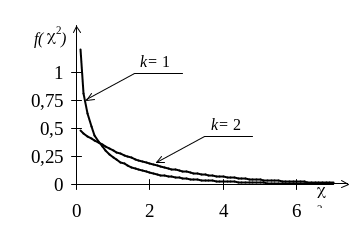
Рис. 24
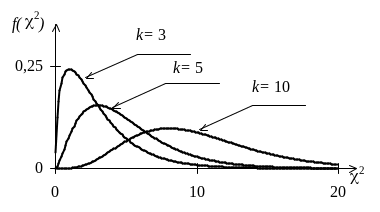
Рис. 25
Можно
показать, что числовые
характеристики
-распределения
с k
степенями свободы
равны:
и
.
С увеличением числа степеней свободы k распределение приближается к нормальному. Это распределение асимметричное (имеет положительную правостороннюю асимметрию). Распределение Пирсона широко используется в математической статистике, в частности при проверке статистических гипотез.
Распределение Стьюдента (t-распределение)
Пусть
Z
- нормированная нормально распределенная
случайная величина, то есть
,
,
а
- случайная величина, не зависящая от Z
и имеющая
распределение
с k
степенями свободы. Тогда случайная
величина
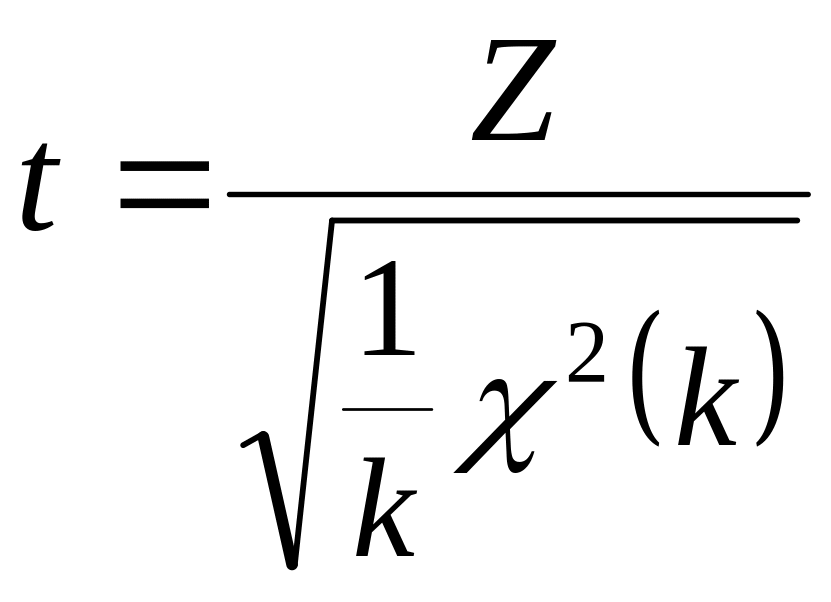имеет распределение Стьюдента2
(t-распределение)
с k
степенями свободы.
Из данного определения следует, что случайная величина t может принимать значения любого знака, а число степеней свободы k является параметром этого распределения.
Функция плотности вероятности t-распределения имеет вид
,
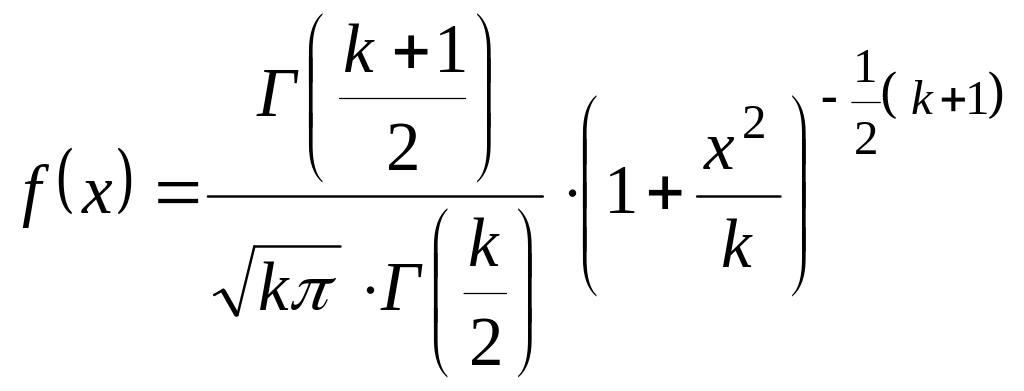где
,
и
- значения гамма-функции.
Числовые
характеристики
распределения Стьюдента:
,
.
Кривая распределения Стьюдента (рис. 26) симметрична относительно оси ординат, как и кривая нормированного нормального распределения, но является более пологой по сравнению с нормированной нормальной кривой.
Рис. 26
С ростом числа степеней свободы k распределение Стьюдента быстро приближается к нормированному нормальному распределению. Это распределение широко применяется в математической статистике, например, при решении задач, когда генеральная совокупность признака имеет нормальный закон распределения. Но его можно использовать и для случаев, когда распределение признака в генеральной совокупности близко к нормальному. Практически при k>30 можно считать t-распределение приближенно нормальным. Кроме того, t-распределение применяется при проверке многих статистических гипотез.